The SEVERITY Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Predefined DistributionsCensoring and TruncationParameter Estimation MethodParameter InitializationEstimating Regression EffectsLevelization of Classification VariablesSpecification and Parameterization of Model EffectsEmpirical Distribution Function Estimation MethodsStatistics of FitDefining a Severity Distribution Model with the FCMP ProcedurePredefined Utility FunctionsScoring FunctionsCustom Objective FunctionsMultithreaded ComputationInput Data SetsOutput Data SetsDisplayed OutputODS Graphics
Predefined DistributionsCensoring and TruncationParameter Estimation MethodParameter InitializationEstimating Regression EffectsLevelization of Classification VariablesSpecification and Parameterization of Model EffectsEmpirical Distribution Function Estimation MethodsStatistics of FitDefining a Severity Distribution Model with the FCMP ProcedurePredefined Utility FunctionsScoring FunctionsCustom Objective FunctionsMultithreaded ComputationInput Data SetsOutput Data SetsDisplayed OutputODS Graphics -
Examples
 Defining a Model for Gaussian DistributionDefining a Model for the Gaussian Distribution with a Scale ParameterDefining a Model for Mixed-Tail DistributionsEstimating Parameters Using Cramér-von Mises EstimatorFitting a Scaled Tweedie Model with RegressorsFitting Distributions to Interval-Censored DataDefining a Finite Mixture Model That Has a Scale ParameterPredicting Mean and Value-at-Risk by Using Scoring FunctionsScale Regression with Rich Regression Effects
Defining a Model for Gaussian DistributionDefining a Model for the Gaussian Distribution with a Scale ParameterDefining a Model for Mixed-Tail DistributionsEstimating Parameters Using Cramér-von Mises EstimatorFitting a Scaled Tweedie Model with RegressorsFitting Distributions to Interval-Censored DataDefining a Finite Mixture Model That Has a Scale ParameterPredicting Mean and Value-at-Risk by Using Scoring FunctionsScale Regression with Rich Regression Effects - References
PROC SEVERITY enables you to estimate model parameters by minimizing your own objective function. This example illustrates
how you can use PROC SEVERITY to implement the Cramér-von Mises estimator. Let ![]() denote the estimate of CDF at
denote the estimate of CDF at ![]() for a distribution with parameters
for a distribution with parameters ![]() , and let
, and let ![]() denote the empirical estimate of CDF (EDF) at
denote the empirical estimate of CDF (EDF) at ![]() that is computed from a sample
that is computed from a sample ![]() ,
, ![]() . Then, the Cramér-von Mises estimator of the parameters is defined as
. Then, the Cramér-von Mises estimator of the parameters is defined as
This estimator belongs to the class of minimum distance estimators. It attempts to estimate the parameters such that the squared distance between the CDF and EDF estimates is minimized.
The following PROC SEVERITY step uses the Cramér-von Mises estimator to fit four candidate distribution models, including the LOGNGPD mixed-tail distribution model that was defined in Defining a Model for Mixed-Tail Distributions. The input sample is the same as is used in that example.
/*--- Set the search path for functions defined with PROC FCMP ---*/ options cmplib=(work.sevexmpl); /*-------- Fit LOGNGPD model with PROC SEVERITY by using ------- -------- the Cramer-von Mises minimum distance estimator -------*/ proc severity data=testmixdist obj=cvmobj print=all plots=pp; loss y; dist logngpd burr logn gpd; * Cramer-von Mises estimator (minimizes the distance * * between parametric and nonparametric estimates) *; cvmobj = _cdf_(y); cvmobj = (cvmobj -_edf_(y))**2; run;
The OBJ= option in the PROC SEVERITY statement specifies that the objective function cvmobj should be minimized. The programming statements compute the contribution of each observation in the input data set to the
objective function cvmobj. The use of keyword functions _CDF_ and _EDF_ makes the program applicable to all the distributions.
Some of the key results prepared by PROC SEVERITY are shown in Output 23.4.1. The "Model Selection" table indicates that all models converged. When you specify a custom objective function, the default selection criterion is the value of the custom objective function. The "All Fit Statistics" table indicates that LOGNGPD is the best distribution according to all the statistics of fit. Comparing the fit statistics of Output 23.4.1 with those of Output 23.3.1 indicates that the use of the Cramér-von Mises estimator has resulted in smaller values for all the EDF-based statistics of fit for all the models, which is expected from a minimum distance estimator.
Output 23.4.1: Summary of Cramér-von Mises Estimation
| All Fit Statistics | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Distribution | cvmobj | -2 Log Likelihood |
AIC | AICC | BIC | KS | AD | CvM | ||||||||
| logngpd | 0.02694 | * | 419.49635 | * | 429.49635 | * | 430.13464 | * | 442.52220 | * | 0.51332 | * | 0.21563 | * | 0.03030 | * |
| Burr | 0.03325 | 436.58823 | 442.58823 | 442.83823 | 450.40374 | 0.53084 | 0.82875 | 0.03807 | ||||||||
| Logn | 0.03633 | 491.88659 | 495.88659 | 496.01030 | 501.09693 | 0.52469 | 2.08312 | 0.04173 | ||||||||
| Gpd | 2.96090 | 560.35409 | 564.35409 | 564.47780 | 569.56443 | 2.99095 | 15.51378 | 2.97806 | ||||||||
| Note: The asterisk (*) marks the best model according to each column's criterion. | ||||||||||||||||
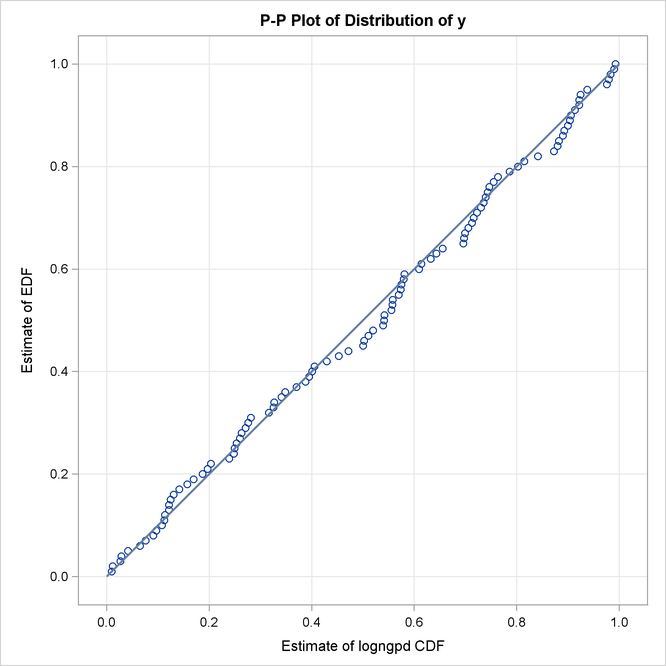
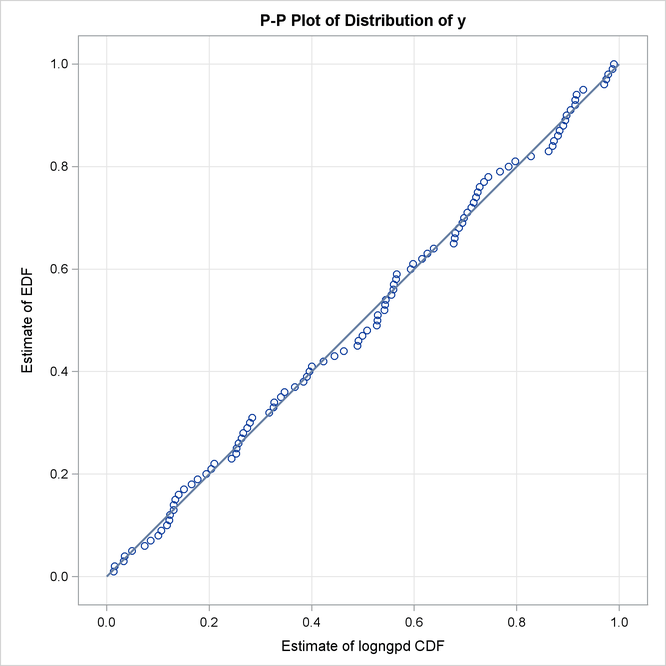
The P-P plots in Output 23.4.2 provide a visual confirmation that the CDF estimates match the EDF estimates more closely when compared to the estimates that are obtained with the maximum likelihood estimator.
Output 23.4.2: P-P Plots for LOGNGPD Model with Maximum Likelihood (Left) and Cramér-von Mises (Right) Estimators
|
|
|