The SEVERITY Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Predefined DistributionsCensoring and TruncationParameter Estimation MethodParameter InitializationEstimating Regression EffectsLevelization of Classification VariablesSpecification and Parameterization of Model EffectsEmpirical Distribution Function Estimation MethodsStatistics of FitDefining a Severity Distribution Model with the FCMP ProcedurePredefined Utility FunctionsScoring FunctionsCustom Objective FunctionsMultithreaded ComputationInput Data SetsOutput Data SetsDisplayed OutputODS Graphics
Predefined DistributionsCensoring and TruncationParameter Estimation MethodParameter InitializationEstimating Regression EffectsLevelization of Classification VariablesSpecification and Parameterization of Model EffectsEmpirical Distribution Function Estimation MethodsStatistics of FitDefining a Severity Distribution Model with the FCMP ProcedurePredefined Utility FunctionsScoring FunctionsCustom Objective FunctionsMultithreaded ComputationInput Data SetsOutput Data SetsDisplayed OutputODS Graphics -
Examples
 Defining a Model for Gaussian DistributionDefining a Model for the Gaussian Distribution with a Scale ParameterDefining a Model for Mixed-Tail DistributionsEstimating Parameters Using Cramér-von Mises EstimatorFitting a Scaled Tweedie Model with RegressorsFitting Distributions to Interval-Censored DataDefining a Finite Mixture Model That Has a Scale ParameterPredicting Mean and Value-at-Risk by Using Scoring FunctionsScale Regression with Rich Regression Effects
Defining a Model for Gaussian DistributionDefining a Model for the Gaussian Distribution with a Scale ParameterDefining a Model for Mixed-Tail DistributionsEstimating Parameters Using Cramér-von Mises EstimatorFitting a Scaled Tweedie Model with RegressorsFitting Distributions to Interval-Censored DataDefining a Finite Mixture Model That Has a Scale ParameterPredicting Mean and Value-at-Risk by Using Scoring FunctionsScale Regression with Rich Regression Effects - References
In some applications, a few severity values tend to be extreme as compared to the typical values. The extreme values represent the worst case scenarios and cannot be discarded as outliers. Instead, their distribution must be modeled to prepare for their occurrences. In such cases, it is often useful to fit one distribution to the non-extreme values and another distribution to the extreme values. The mixed-tail distribution mixes two distributions: one for the body region, which contains the non-extreme values, and another for the tail region, which contains the extreme values. The tail distribution is usually a generalized Pareto distribution (GPD), because it is usually good for modeling the conditional excess severity above a threshold. The body distribution can be any distribution. The following definitions are used in describing a generic formulation of a mixed-tail distribution:
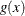
-
PDF of the body distribution
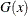
-
CDF of the body distribution
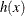
-
PDF of the tail distribution
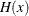
-
CDF of the tail distribution
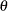
-
scale parameter for the body distribution
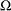
-
set of nonscale parameters for the body distribution
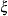
-
shape parameter for the GPD tail distribution
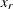
-
normalized value of the response variable at which the tail starts
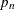
-
mixing probability
Given these notations, the PDF ![]() and the CDF
and the CDF ![]() of the mixed-tail distribution are defined as
of the mixed-tail distribution are defined as
where ![]() is the value of the response variable at which the tail starts.
is the value of the response variable at which the tail starts.
These definitions indicate the following:
-
The body distribution is conditional on
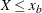 , where X denotes the random response variable.
, where X denotes the random response variable.
-
The tail distribution is the generalized Pareto distribution of the
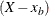 values.
values.
-
The probability that a response variable value belongs to the body is
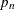 . Consequently the probability that the value belongs to the tail is
. Consequently the probability that the value belongs to the tail is 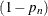 .
.
The parameters of this distribution are ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . The scale of the GPD tail distribution
. The scale of the GPD tail distribution ![]() is computed as
is computed as
The parameter ![]() is usually estimated using a tail index estimation algorithm. One such algorithm is the Hill’s algorithm (Danielsson et al.,
2001), which is implemented by the predefined utility function SVRTUTIL_HILLCUTOFF available to you in the
is usually estimated using a tail index estimation algorithm. One such algorithm is the Hill’s algorithm (Danielsson et al.,
2001), which is implemented by the predefined utility function SVRTUTIL_HILLCUTOFF available to you in the Sashelp.Svrtdist library. The algorithm and the utility function are described in detail in the section Predefined Utility Functions. The function computes an estimate of ![]() , which can be used to compute an estimate of
, which can be used to compute an estimate of ![]() because
because ![]() , where
, where ![]() is the estimate of the scale parameter of the body distribution.
is the estimate of the scale parameter of the body distribution.
The parameter ![]() is usually determined by the domain expert based on the fraction of losses that are expected to belong to the tail.
is usually determined by the domain expert based on the fraction of losses that are expected to belong to the tail.
The following SAS statements define the LOGNGPD distribution model for a mixed-tail distribution with the lognormal distribution as the body distribution and GPD as the tail distribution:
/*------- Define Lognormal Body-GPD Tail Mixed Distribution -------*/
proc fcmp library=sashelp.svrtdist outlib=work.sevexmpl.models;
function LOGNGPD_DESCRIPTION() $256;
length desc $256;
desc1 = "Lognormal Body-GPD Tail Distribution.";
desc2 = " Mu, Sigma, and Xi are free parameters.";
desc3 = " Xr and Pn are constant parameters.";
desc = desc1 || desc2 || desc3;
return(desc);
endsub;
function LOGNGPD_SCALETRANSFORM() $3;
length xform $3;
xform = "LOG";
return (xform);
endsub;
subroutine LOGNGPD_CONSTANTPARM(Xr,Pn);
endsub;
function LOGNGPD_PDF(x, Mu,Sigma,Xi,Xr,Pn);
cutoff = exp(Mu) * Xr;
p = CDF('LOGN',cutoff, Mu, Sigma);
if (x < cutoff + constant('MACEPS')) then do;
return ((Pn/p)*PDF('LOGN', x, Mu, Sigma));
end;
else do;
gpd_scale = p*((1-Pn)/Pn)/PDF('LOGN', cutoff, Mu, Sigma);
h = (1+Xi*(x-cutoff)/gpd_scale)**(-1-(1/Xi))/gpd_scale;
return ((1-Pn)*h);
end;
endsub;
function LOGNGPD_CDF(x, Mu,Sigma,Xi,Xr,Pn);
cutoff = exp(Mu) * Xr;
p = CDF('LOGN',cutoff, Mu, Sigma);
if (x < cutoff + constant('MACEPS')) then do;
return ((Pn/p)*CDF('LOGN', x, Mu, Sigma));
end;
else do;
gpd_scale = p*((1-Pn)/Pn)/PDF('LOGN', cutoff, Mu, Sigma);
H = 1 - (1 + Xi*((x-cutoff)/gpd_scale))**(-1/Xi);
return (Pn + (1-Pn)*H);
end;
endsub;
subroutine LOGNGPD_PARMINIT(dim,x[*],nx[*],F[*],Ftype,
Mu,Sigma,Xi,Xr,Pn);
outargs Mu,Sigma,Xi,Xr,Pn;
array xe[1] / nosymbols;
array nxe[1] / nosymbols;
eps = constant('MACEPS');
Pn = 0.8; /* Set mixing probability */
_status_ = .;
call streaminit(56789);
Xb = svrtutil_hillcutoff(dim, x, 100, 25, _status_);
if (missing(_status_) or _status_ = 1) then
Xb = svrtutil_percentile(Pn, dim, x, F, Ftype);
/* prepare arrays for excess values */
i = 1;
do while (i <= dim and x[i] < Xb+eps);
i = i + 1;
end;
dime = dim-i+1;
call dynamic_array(xe, dime);
call dynamic_array(nxe, dime);
j = 1;
do while(i <= dim);
xe[j] = x[i] - Xb;
nxe[j] = nx[i];
i = i + 1;
j = j + 1;
end;
/* Initialize lognormal parameters */
call logn_parminit(dim, x, nx, F, Ftype, Mu, Sigma);
if (not(missing(Mu))) then
Xr = Xb/exp(Mu);
else
Xr = .;
/* Initialize GPD's shape parameter using excess values */
call gpd_parminit(dime, xe, nxe, F, Ftype, theta_gpd, Xi);
endsub;
subroutine LOGNGPD_LOWERBOUNDS(Mu,Sigma,Xi,Xr,Pn);
outargs Mu,Sigma,Xi,Xr,Pn;
Mu = .; /* Mu has no lower bound */
Sigma = 0; /* Sigma > 0 */
Xi = 0; /* Xi > 0 */
endsub;
quit;
Note the following points about the LOGNGPD definition:
-
The parameters
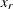 and
and 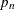 are not estimated with the maximum likelihood method used by PROC SEVERITY, so you need to specify them as constant parameters by defining the dist_CONSTANTPARM
subroutine. The signature of LOGNGPD_CONSTANTPARM subroutine lists only the constant parameters Xr and Pn.
are not estimated with the maximum likelihood method used by PROC SEVERITY, so you need to specify them as constant parameters by defining the dist_CONSTANTPARM
subroutine. The signature of LOGNGPD_CONSTANTPARM subroutine lists only the constant parameters Xr and Pn.
-
The parameter
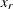 is estimated by first using the SVRTUTIL_HILLCUTOFF utility function to compute an estimate of the cutoff point
is estimated by first using the SVRTUTIL_HILLCUTOFF utility function to compute an estimate of the cutoff point 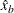 and then computing
and then computing 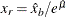 . If SVRTUTIL_HILLCUTOFF fails to compute a valid estimate, then the SVRTUTIL_PERCENTILE utility function is used to set
. If SVRTUTIL_HILLCUTOFF fails to compute a valid estimate, then the SVRTUTIL_PERCENTILE utility function is used to set 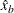 to the
to the 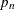 th percentile of the data. The parameter
th percentile of the data. The parameter 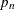 is fixed to 0.8.
is fixed to 0.8.
-
The
Sashelp.Svrtdistlibrary is specified with the LIBRARY= option in the PROC FCMP statement to enable the LOGNGPD_PARMINIT subroutine to use the predefined utility functions (SVRTUTIL_HILLCUTOFF and SVRTUTIL_PERCENTILE) and parameter initialization subroutines (LOGN_PARMINIT and GPD_PARMINIT). -
The LOGNGPD_LOWERBOUNDS subroutine defines the lower bounds for all parameters. This subroutine is required because the parameter Mu has a non-default lower bound. The bounds for Sigma and Xi must be specified. If they are not specified, they are returned as missing values, which PROC SEVERITY interprets as having no lower bound. You need not specify any bounds for the constant parameters Xr and Pn, because they are not subject to optimization.
The following DATA step statements simulate a sample from a mixed-tail distribution with a lognormal body and GPD tail. The
parameter ![]() is fixed to 0.8, the same value used in the LOGNGPD_PARMINIT subroutine defined previously.
is fixed to 0.8, the same value used in the LOGNGPD_PARMINIT subroutine defined previously.
/*----- Simulate a sample for the mixed-tail distribution -----*/
data testmixdist(keep=y label='Lognormal Body-GPD Tail Sample');
call streaminit(45678);
label y='Response Variable';
N = 100;
Mu = 1.5;
Sigma = 0.25;
Xi = 1.5;
Pn = 0.8;
/* Generate data comprising the lognormal body */
Nbody = N*Pn;
do i=1 to Nbody;
y = exp(Mu) * rand('LOGNORMAL')**Sigma;
output;
end;
/* Generate data comprising the GPD tail */
cutoff = quantile('LOGNORMAL', Pn, Mu, Sigma);
gpd_scale = (1-Pn) / pdf('LOGNORMAL', cutoff, Mu, Sigma);
do i=Nbody+1 to N;
y = cutoff + ((1-rand('UNIFORM'))**(-Xi) - 1)*gpd_scale/Xi;
output;
end;
run;
The following statements use PROC SEVERITY to fit the LOGNGPD distribution model to the simulated sample. They also fit three
other predefined distributions (BURR, LOGN, and GPD). The final parameter estimates are written to the Work.Parmest data set.
/*--- Set the search path for functions defined with PROC FCMP ---*/
options cmplib=(work.sevexmpl);
/*-------- Fit LOGNGPD model with PROC SEVERITY --------*/
proc severity data=testmixdist print=all plots(histogram kernel)=all
outest=parmest;
loss y;
dist logngpd burr logn gpd;
run;
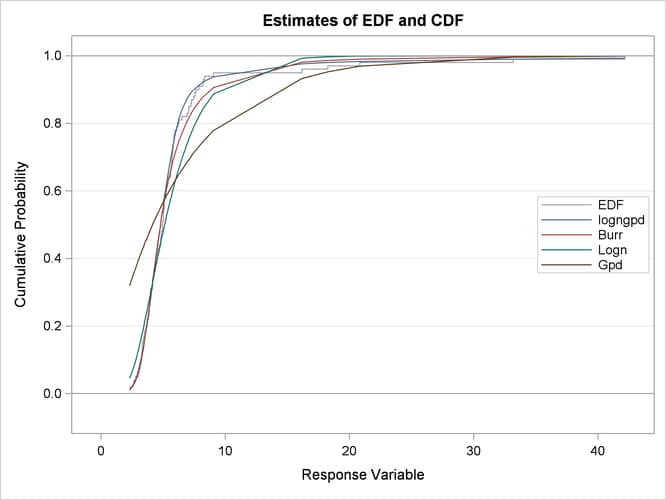
Some of the results prepared by PROC SEVERITY are shown in Output 23.3.1 through Output 23.3.4. The "Model Selection" table in Output 23.3.1 indicates that all models converged. The last table in Output 23.3.1 shows that the model with LOGNGPD distribution has the best fit according to almost all the statistics of fit. The Burr distribution model is the closest contender to the LOGNGPD model, but the GPD distribution model fits the data very poorly.
Output 23.3.1: Summary of Fitting Mixed-Tail Distribution
| All Fit Statistics | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Distribution | -2 Log Likelihood |
AIC | AICC | BIC | KS | AD | CvM | |||||||
| logngpd | 418.78232 | * | 428.78232 | * | 429.42062 | * | 441.80817 | 0.62140 | * | 0.31670 | * | 0.04972 | * | |
| Burr | 424.93728 | 430.93728 | 431.18728 | 438.75280 | * | 0.71373 | 0.57649 | 0.07860 | ||||||
| Logn | 459.43471 | 463.43471 | 463.55842 | 468.64505 | 1.55267 | 3.27122 | 0.48448 | |||||||
| Gpd | 558.13444 | 562.13444 | 562.25815 | 567.34478 | 3.43470 | 16.74156 | 3.31860 | |||||||
| Note: The asterisk (*) marks the best model according to each column's criterion. | ||||||||||||||
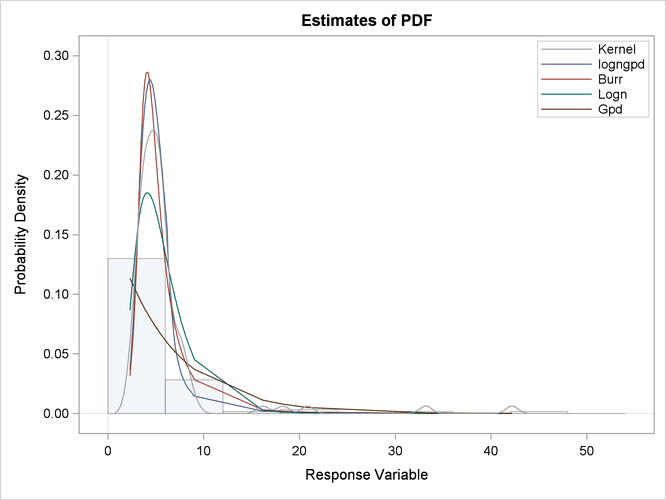
The plots in Output 23.3.2 show that both the lognormal and GPD distributions fit the data poorly, GPD being the worst. The Burr distribution fits the data as well as the LOGNGPD distribution in the body region, but has a poorer fit in the tail region than the LOGNGPD distribution.
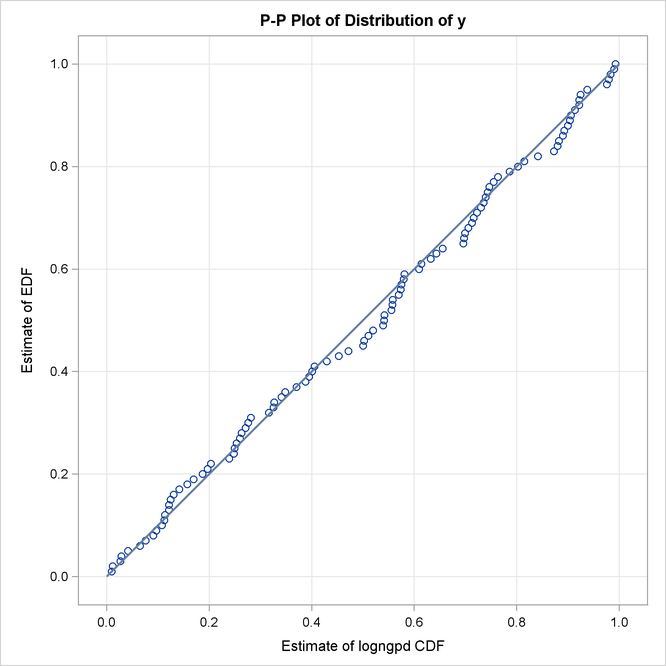
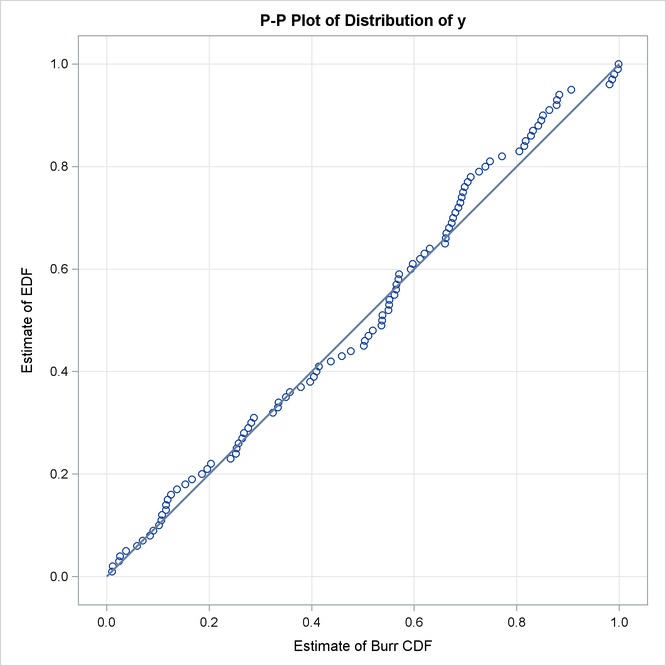
The P-P plots of Output 23.3.3 provide a better visual confirmation that the LOGNGPD distribution fits the tail region better than the Burr distribution.
The detailed results for the LOGNGPD distribution are shown in Output 23.3.4. The initial values table indicates the values computed by LOGNGPD_PARMINIT subroutine for the Xr and Pn parameters. It also uses the bounds columns to indicate the constant parameters. The last table in the figure shows the final parameter estimates. The estimates of all free parameters are significantly different from 0. As expected, the final estimates of the constant parameters Xr and Pn have not changed from their initial values.
The following SAS statements use the parameter estimates to compute the value where the tail region is estimated to start
(![]() ) and the scale of the GPD tail distribution (
) and the scale of the GPD tail distribution (![]() ):
):
/*-------- Compute tail cutoff and tail distribution's scale --------*/
data xb_thetat(keep=x_b theta_t);
set parmest(where=(_MODEL_='logngpd' and _TYPE_='EST'));
x_b = exp(Mu) * Xr;
theta_t = (CDF('LOGN',x_b,Mu,Sigma)/PDF('LOGN',x_b,Mu,Sigma)) *
((1-Pn)/Pn);
run;
proc print data=xb_thetat noobs;
run;
The computed values of ![]() and
and ![]() are shown as x_b and theta_t in Output 23.3.5. Equipped with this additional derived information, you can now interpret the results of fitting the mixed-tail distribution
as follows:
are shown as x_b and theta_t in Output 23.3.5. Equipped with this additional derived information, you can now interpret the results of fitting the mixed-tail distribution
as follows:
-
The tail starts at
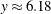 . The primary benefit of using the scale-normalized cutoff (
. The primary benefit of using the scale-normalized cutoff (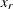 ) as the constant parameter instead of using the actual cutoff (
) as the constant parameter instead of using the actual cutoff (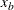 ) is that the absolute cutoff gets optimized by virtue of optimizing the scale of the body region (
) is that the absolute cutoff gets optimized by virtue of optimizing the scale of the body region (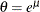 ).
).
-
The values
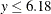 follow the lognormal distribution with parameters
follow the lognormal distribution with parameters 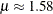 and
and 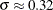 . These parameter estimates are reasonably close to the parameters used for simulating the sample.
. These parameter estimates are reasonably close to the parameters used for simulating the sample.
-
The values
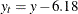 (
(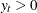 ) follow the GPD distribution with scale
) follow the GPD distribution with scale 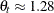 and shape
and shape 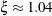 .
.