The OPTLP Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Data Input and OutputPresolvePricing Strategies for the Primal and Dual Simplex AlgorithmsWarm Start for the Primal and Dual Simplex AlgorithmsThe Network Simplex AlgorithmThe Interior Point AlgorithmIteration Log for the Primal and Dual Simplex AlgorithmsIteration Log for the Network Simplex AlgorithmIteration Log for the Interior Point AlgorithmIteration Log for the Crossover AlgorithmConcurrent LPParallel ProcessingODS TablesIrreducible Infeasible SetMacro Variable _OROPTLP_
Data Input and OutputPresolvePricing Strategies for the Primal and Dual Simplex AlgorithmsWarm Start for the Primal and Dual Simplex AlgorithmsThe Network Simplex AlgorithmThe Interior Point AlgorithmIteration Log for the Primal and Dual Simplex AlgorithmsIteration Log for the Network Simplex AlgorithmIteration Log for the Interior Point AlgorithmIteration Log for the Crossover AlgorithmConcurrent LPParallel ProcessingODS TablesIrreducible Infeasible SetMacro Variable _OROPTLP_ -
Examples

- References
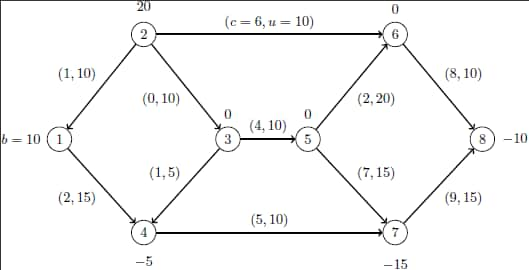
This example demonstrates how to use the network simplex algorithm to find the minimum-cost flow in a directed graph. Consider the directed graph in Figure 12.5, which appears in Ahuja, Magnanti, and Orlin (1993).
You can use the following SAS statements to create the input data set ex8:
data ex8; input field1 $8. field2 $13. @25 field3 $13. field4 @53 field5 $13. field6; datalines; NAME . . . . . ROWS . . . . . N obj . . . . E balance['1'] . . . . E balance['2'] . . . . E balance['3'] . . . . E balance['4'] . . . . E balance['5'] . . . . E balance['6'] . . . . E balance['7'] . . . . E balance['8'] . . . . COLUMNS . . . . . . x['1','4'] obj 2 balance['1'] 1 . x['1','4'] balance['4'] -1 . . . x['2','1'] obj 1 balance['1'] -1 . x['2','1'] balance['2'] 1 . . . x['2','3'] balance['2'] 1 balance['3'] -1 . x['2','6'] obj 6 balance['2'] 1 . x['2','6'] balance['6'] -1 . . . x['3','4'] obj 1 balance['3'] 1 . x['3','4'] balance['4'] -1 . . . x['3','5'] obj 4 balance['3'] 1 . x['3','5'] balance['5'] -1 . . . x['4','7'] obj 5 balance['4'] 1 . x['4','7'] balance['7'] -1 . . . x['5','6'] obj 2 balance['5'] 1 . x['5','6'] balance['6'] -1 . . . x['5','7'] obj 7 balance['5'] 1 . x['5','7'] balance['7'] -1 . . . x['6','8'] obj 8 balance['6'] 1 . x['6','8'] balance['8'] -1 . . . x['7','8'] obj 9 balance['7'] 1 . x['7','8'] balance['8'] -1 . . RHS . . . . . . .RHS. balance['1'] 10 . . . .RHS. balance['2'] 20 . . . .RHS. balance['4'] -5 . . . .RHS. balance['7'] -15 . . . .RHS. balance['8'] -10 . . BOUNDS . . . . . UP .BOUNDS. x['1','4'] 15 . . UP .BOUNDS. x['2','1'] 10 . . UP .BOUNDS. x['2','3'] 10 . . UP .BOUNDS. x['2','6'] 10 . . UP .BOUNDS. x['3','4'] 5 . . UP .BOUNDS. x['3','5'] 10 . . UP .BOUNDS. x['4','7'] 10 . . UP .BOUNDS. x['5','6'] 20 . . UP .BOUNDS. x['5','7'] 15 . . UP .BOUNDS. x['6','8'] 10 . . UP .BOUNDS. x['7','8'] 15 . . ENDATA . . . . . ;
You can use the following call to PROC OPTLP to find the minimum-cost flow:
proc optlp presolver = none printlevel = 2 logfreq = 1 data = ex8 primalout = ex8out algorithm = ns; run;
The optimal solution is displayed in Output 12.8.1.
Output 12.8.1: Network Simplex Algorithm: Primal Solution Output
| Primal Solution |
| Obs | Objective Function ID |
RHS ID | Variable Name | Variable Type |
Objective Coefficient |
Lower Bound |
Upper Bound | Variable Value |
Variable Status |
Reduced Cost |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | obj | .RHS. | x['1','4'] | D | 2 | 0 | 15 | 10 | B | 0 |
| 2 | obj | .RHS. | x['2','1'] | D | 1 | 0 | 10 | 0 | L | 2 |
| 3 | obj | .RHS. | x['2','3'] | D | 0 | 0 | 10 | 10 | B | 0 |
| 4 | obj | .RHS. | x['2','6'] | D | 6 | 0 | 10 | 10 | B | 0 |
| 5 | obj | .RHS. | x['3','4'] | D | 1 | 0 | 5 | 5 | B | 0 |
| 6 | obj | .RHS. | x['3','5'] | D | 4 | 0 | 10 | 5 | B | 0 |
| 7 | obj | .RHS. | x['4','7'] | D | 5 | 0 | 10 | 10 | U | -5 |
| 8 | obj | .RHS. | x['5','6'] | D | 2 | 0 | 20 | 0 | L | 0 |
| 9 | obj | .RHS. | x['5','7'] | D | 7 | 0 | 15 | 5 | B | 0 |
| 10 | obj | .RHS. | x['6','8'] | D | 8 | 0 | 10 | 10 | B | 0 |
| 11 | obj | .RHS. | x['7','8'] | D | 9 | 0 | 15 | 0 | L | 6 |
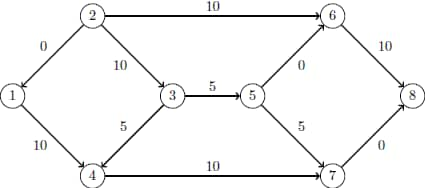
The optimal solution is represented graphically in Figure 12.6.
The iteration log is displayed in Output 12.8.2.
Output 12.8.2: Log: Solution Progress
| NOTE: The OPTLP procedure is executing in single-machine mode. |
| NOTE: The problem has 11 variables (0 free, 0 fixed). |
| NOTE: The problem has 8 constraints (0 LE, 8 EQ, 0 GE, 0 range). |
| NOTE: The problem has 22 constraint coefficients. |
| NOTE: The LP presolver value NONE is applied. |
| NOTE: The LP solver is called. |
| NOTE: The Network Simplex algorithm is used. |
| NOTE: The network has 8 rows (100.00%), 11 columns (100.00%), and 1 component. |
| NOTE: The network extraction and setup time is 0.00 seconds. |
| Primal Primal Dual |
| Iteration Objective Infeasibility Infeasibility Time |
| 1 0.000000E+00 2.000000E+01 8.900000E+01 0.00 |
| 2 0.000000E+00 2.000000E+01 8.900000E+01 0.00 |
| 3 5.000000E+00 1.500000E+01 8.400000E+01 0.00 |
| 4 5.000000E+00 1.500000E+01 8.300000E+01 0.00 |
| 5 7.500000E+01 1.500000E+01 8.300000E+01 0.00 |
| 6 7.500000E+01 1.500000E+01 7.900000E+01 0.00 |
| 7 1.300000E+02 1.000000E+01 7.600000E+01 0.00 |
| 8 2.700000E+02 0.000000E+00 0.000000E+00 0.00 |
| NOTE: The Network Simplex solve time is 0.00 seconds. |
| NOTE: The total Network Simplex solve time is 0.00 seconds. |
| NOTE: Optimal. |
| NOTE: Objective = 270. |
| NOTE: The data set WORK.EX8OUT has 11 observations and 10 variables. |