The GLIMMIX Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function
PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function -
Details
 Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance (Sandwich) EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics
Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance (Sandwich) EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics -
Examples
 Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary Data
Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary Data - References
Example 41.13 Response Surface Comparisons with Multiplicity Adjustments
Koch et al. (1990) present data for a multicenter clinical trial testing the efficacy of a respiratory drug in patients with respiratory disease.
Within each of two centers, patients were randomly assigned to a placebo (P) or an active (A) treatment. Prior to treatment
and at four follow-up visits, patient status was recorded in one of five ordered categories (0=terrible, 1=poor, …, 4=excellent).
The following DATA step creates the SAS data set clinical for this study.
data Clinical;
do Center = 1, 2;
do Gender = 'F','M';
do Drug = 'A','P';
input nPatient @@;
do iPatient = 1 to nPatient;
input ID Age (t0-t4) (1.) @@;
output;
end;
end;
end;
end;
datalines;
2 53 32 12242 18 47 22344
5 5 13 44444 19 31 21022 25 35 10000 28 36 23322
36 45 22221
25 54 11 44442 12 14 23332 51 15 02333 20 20 33231
16 22 12223 50 22 21344 3 23 33443 32 23 23444
56 25 23323 35 26 12232 26 26 22222 21 26 24142
8 28 12212 30 28 00121 33 30 33442 11 30 34443
42 31 12311 9 31 33444 37 31 02321 23 32 34433
6 34 11211 22 46 43434 24 48 23202 38 50 22222
48 57 33434
24 43 13 34444 41 14 22123 34 15 22332 29 19 23300
15 20 44444 13 23 33111 27 23 44244 55 24 34443
17 25 11222 45 26 24243 40 26 12122 44 27 12212
49 27 33433 39 23 21111 2 28 20000 14 30 10000
31 37 10000 10 37 32332 7 43 23244 52 43 11132
4 44 34342 1 46 22222 46 49 22222 47 63 22222
4 30 37 13444 52 39 23444 23 60 44334 54 63 44444
12 28 31 34444 5 32 32234 21 36 33213 50 38 12000
1 39 12112 48 39 32300 7 44 34444 38 47 23323
8 48 22100 11 48 22222 4 51 34244 17 58 14220
23 12 13 44444 10 14 14444 27 19 33233 47 20 24443
16 20 21100 29 21 33444 20 24 44444 25 25 34331
15 25 34433 2 25 22444 9 26 23444 49 28 23221
55 31 44444 43 34 24424 26 35 44444 14 37 43224
36 41 34434 51 43 33442 37 52 12122 19 55 44444
32 55 22331 3 58 44444 53 68 23334
16 39 11 34444 40 14 21232 24 15 32233 41 15 43334
33 19 42233 34 20 32444 13 20 14444 45 33 33323
22 36 24334 18 38 43000 35 42 32222 44 43 21000
6 45 34212 46 48 44000 31 52 23434 42 66 33344
;
Westfall and Tobias (2007) define as the measure of efficacy the average of the ratings at the final two visits and model this average as a function
of drug, baseline assessment score, and age. Hence, in their model, the expected efficacy for drug ![]() can be written as
can be written as
|
|
where t is the baseline (pretreatment) assessment score and a is the patient’s age at baseline. The age range for these data extends from 11 to 68 years. Suppose that the scientific question
of interest is the comparison of the two response surfaces at a set of values ![]() . In other words, you want to know for which values of the covariates the average response differs significantly between the
treatment group and the placebo group. If the set of ages of interest is
. In other words, you want to know for which values of the covariates the average response differs significantly between the
treatment group and the placebo group. If the set of ages of interest is ![]() , then this involves
, then this involves ![]() comparisons, a massive multiple testing problem. The large number of comparisons and the fact that the set
comparisons, a massive multiple testing problem. The large number of comparisons and the fact that the set ![]() is chosen somewhat arbitrarily require the application of multiplicity corrections in order to protect the familywise Type
I error across the comparisons.
is chosen somewhat arbitrarily require the application of multiplicity corrections in order to protect the familywise Type
I error across the comparisons.
When testing hypotheses that have logical restrictions, the power of multiplicity corrected tests can be increased by taking
the restrictions into account. Logical restrictions exist, for example, when not all hypotheses in a set can be simultaneously
true. Westfall and Tobias (2007) extend the truncated closed testing procedure (TCTP) of Royen (1989) for pairwise comparisons in ANOVA to general contrasts. Their work is also an extension of the S2 method of Shaffer (1986); see also Westfall (1997). These methods are all monotonic in the (unadjusted) p-values of the individual tests, in the sense that if ![]() then the multiple test will never retain
then the multiple test will never retain ![]() while rejecting
while rejecting ![]() . In terms of multiplicity-adjusted p-values
. In terms of multiplicity-adjusted p-values ![]() , monotonicity means that if
, monotonicity means that if ![]() , then
, then ![]() .
.
Analysis as Normal Data with Averaged Endpoints
In order to apply the extended TCTP procedure of Westfall and Tobias (2007) to the problem of comparing response surfaces in the clinical trial, the following convenience macro is helpful to generate the comparisons for the ESTIMATE statement in PROC GLIMMIX:
%macro Contrast(from,to,byA,byT);
%let nCmp = 0;
%do age = &from %to &to %by &byA;
%do t0 = 0 %to 4 %by &byT;
%let nCmp = %eval(&nCmp+1);
%end;
%end;
%let iCmp = 0;
%do age = &from %to &to %by &byA;
%do t0 = 0 %to 4 %by &byT;
%let iCmp = %eval(&iCmp+1);
"%trim(%left(&age)) %trim(%left(&t0))"
drug 1 -1
drug*age &age -&age
drug*t0 &t0 -&t0
%if (&icmp < &nCmp) %then %do; , %end;
%end;
%end;
%mend;
The following GLIMMIX statements fit the model to the data and compute the 105 contrasts that compare the placebo to the active response at 105 points in the two-dimensional regressor space:
proc glimmix data=clinical;
t = (t3+t4)/2;
class drug;
model t = drug t0 age drug*age drug*t0;
estimate %contrast(10,70,3,1)
/ adjust=simulate(seed=1)
stepdown(type=logical);
ods output Estimates=EstStepDown;
run;
Note that only a single ESTIMATE statement is used. Each of the 105 comparisons is one comparison in the multirow statement. The ADJUST option in the ESTIMATE statement requests multiplicity-adjusted p-values. The extended TCTP method is applied by specifying the STEPDOWN(TYPE=LOGICAL) option to compute step-down-adjusted p-values where logical constraints among the hypotheses are taken into account. The results from the ESTIMATE statement are saved to a data set for subsequent processing. Note also that the response, the average of the ratings at the final two visits, is computed with programming statements in PROC GLIMMIX.
The following statements print the 20 most significant estimated differences (Output 41.13.1):
proc sort data=EstStepDown; by Probt; run; proc print data=EstStepDown(obs=20); var Label Estimate StdErr Probt AdjP; run;
Output 41.13.1: The First 20 Observations of the Estimates Data Set
| Obs | Label | Estimate | StdErr | Probt | Adjp |
|---|---|---|---|---|---|
| 1 | 37 2 | 0.8310 | 0.2387 | 0.0007 | 0.0071 |
| 2 | 40 2 | 0.8813 | 0.2553 | 0.0008 | 0.0071 |
| 3 | 34 2 | 0.7806 | 0.2312 | 0.0010 | 0.0071 |
| 4 | 43 2 | 0.9316 | 0.2794 | 0.0012 | 0.0071 |
| 5 | 46 2 | 0.9819 | 0.3093 | 0.0020 | 0.0071 |
| 6 | 31 2 | 0.7303 | 0.2338 | 0.0023 | 0.0081 |
| 7 | 49 2 | 1.0322 | 0.3434 | 0.0033 | 0.0107 |
| 8 | 52 2 | 1.0825 | 0.3807 | 0.0054 | 0.0167 |
| 9 | 40 3 | 0.7755 | 0.2756 | 0.0059 | 0.0200 |
| 10 | 37 3 | 0.7252 | 0.2602 | 0.0063 | 0.0201 |
| 11 | 43 3 | 0.8258 | 0.2982 | 0.0066 | 0.0201 |
| 12 | 28 2 | 0.6800 | 0.2461 | 0.0068 | 0.0215 |
| 13 | 55 2 | 1.1329 | 0.4202 | 0.0082 | 0.0239 |
| 14 | 46 3 | 0.8761 | 0.3265 | 0.0085 | 0.0239 |
| 15 | 34 3 | 0.6749 | 0.2532 | 0.0089 | 0.0257 |
| 16 | 43 1 | 1.0374 | 0.3991 | 0.0107 | 0.0329 |
| 17 | 46 1 | 1.0877 | 0.4205 | 0.0111 | 0.0329 |
| 18 | 49 3 | 0.9264 | 0.3591 | 0.0113 | 0.0329 |
| 19 | 40 1 | 0.9871 | 0.3827 | 0.0113 | 0.0329 |
| 20 | 58 2 | 1.1832 | 0.4615 | 0.0118 | 0.0329 |
Notice that the adjusted p-values (Adjp) are larger than the unadjusted p-values, as expected. Also notice that several comparisons share the same adjusted p-values. This is a result of the monotonicity of the extended TCTP method.
In order to compare the step-down-adjusted p-values to adjusted p-values that do not use step-down methods, replace the ESTIMATE statement in the previous statements with the following:
estimate %contrast2(10,70,3,1) / adjust=simulate(seed=1); ods output Estimates=EstAdjust;
The following GLIMMIX invocations create output data sets named EstAdjust and EstUnAdjust that contain (non-step-down-) adjusted and unadjusted p-values:
proc glimmix data=clinical;
t = (t3+t4)/2;
class drug;
model t = drug t0 age drug*age drug*t0;
estimate %contrast(10,70,3,1)
/ adjust=simulate(seed=1);
ods output Estimates=EstAdjust;
run;
proc glimmix data=clinical;
t = (t3+t4)/2;
class drug;
model t = drug t0 age drug*age drug*t0;
estimate %contrast(10,70,3,1);
ods output Estimates=EstUnAdjust;
run;
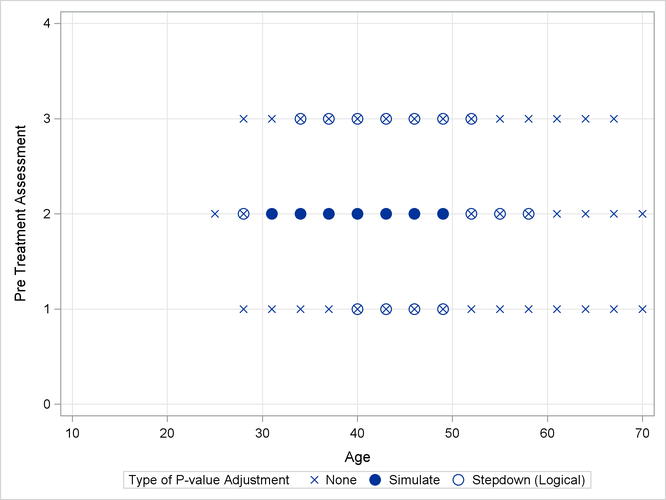
Output 41.13.2 shows a comparison of the significant comparisons (p < 0.05) based on unadjusted, adjusted, and step-down (TCTP) adjusted p-values. Clearly, the unadjusted results indicate the most significant results, but without protecting the Type I error rate for the group of tests. The adjusted p-values (filled circles) lead to a much smaller region in which the response surfaces between treatment and placebo are significantly different. The increased power of the TCTP procedure (open circles) over the standard multiplicity adjustment—without sacrificing Type I error protection—can be seen in the considerably larger region covered by the open circles.
Output 41.13.2: Comparison of Significance Regions
Ordinal Repeated Measure Analysis
The outcome variable in this clinical trial is an ordinal rating of patients in categories 0=terrible, 1=poor, 2=fair, 3=good, and 4=excellent. Furthermore, the observations from repeat visits for the same patients are likely correlated. The previous analysis removes the repeated measures aspect by defining efficacy as the average score at the final two visits. These averages are not normally distributed, however. The response surfaces for the two study arms can also be compared based on a model for ordinal data that takes correlation into account through random effects. Keeping with the theme of the previous analysis, the focus here for illustrative purposes is on the final two visits, and the pretreatment assessment score serves as a covariate in the model.
The following DATA step rearranges the data from the third and fourth on-treatment visits in univariate form with separate observations for the visits by patient:
data clinical_uv;
set clinical;
array time{2} t3-t4;
do i=1 to 2; rating = time{i}; output; end;
run;
The basic model for the analysis is a proportional odds model with cumulative logit link (McCullagh, 1980) and J = 5 categories. In this model, separate intercepts (cutoffs) are modeled for the first ![]() cumulative categories and the intercepts are monotonically increasing. This guarantees ordering of the cumulative probabilities
and nonnegative category probabilities. Using the same covariate structure as in the previous analysis, the probability to
observe a rating in at most category
cumulative categories and the intercepts are monotonically increasing. This guarantees ordering of the cumulative probabilities
and nonnegative category probabilities. Using the same covariate structure as in the previous analysis, the probability to
observe a rating in at most category ![]() is
is
|
|
|
|
|
|
Because only the intercepts are dependent on the category, contrasts comparing regression coefficients can be formulated in
standard fashion. To accommodate the random and covariance structure of the repeated measures model, a random intercept ![]() is applied to the observations for each patient:
is applied to the observations for each patient:
|
|
|
|
|
|
|
|
|
The shared random effect of the two observations creates a marginal correlation. Note that the random effects do not depend on category.
The following GLIMMIX statements fit this ordinal repeated measures model by maximum likelihood via the Laplace approximation and compute TCTP-adjusted p-values for the 105 estimates:
proc glimmix data=clinical_uv method=laplace;
class center id drug;
model rating = drug t0 age drug*age drug*t0 /
dist=multinomial link=cumlogit;
random intercept / subject=id(center);
covtest 0;
estimate %contrast(10,70,3,1)
/ adjust=simulate(seed=1)
stepdown(type=logical);
ods output Estimates=EstStepDownMulti;
run;
The combination of DIST=MULTINOMIAL and LINK=CUMLOGIT requests the proportional odds model. The SUBJECT= effect nests patient IDs within centers, because patient IDs in the data set clinical are not unique within centers. (Specifying SUBJECT=ID*CENTER would have the same effect.) The COVTEST statement requests a likelihood ratio test for the significance of the random patient effect.
The estimate of the variance component for the random patient effect is substantial (Output 41.13.3), but so is its standard error.
Output 41.13.3: Model and Covariance Parameter Information
| Model Information | |
|---|---|
| Data Set | WORK.CLINICAL_UV |
| Response Variable | rating |
| Response Distribution | Multinomial (ordered) |
| Link Function | Cumulative Logit |
| Variance Function | Default |
| Variance Matrix Blocked By | ID(Center) |
| Estimation Technique | Maximum Likelihood |
| Likelihood Approximation | Laplace |
| Degrees of Freedom Method | Containment |
| Covariance Parameter Estimates | |||
|---|---|---|---|
| Cov Parm | Subject | Estimate | Standard Error |
| Intercept | ID(Center) | 10.3483 | 3.2599 |
| Tests of Covariance Parameters Based on the Likelihood |
|||||
|---|---|---|---|---|---|
| Label | DF | -2 Log Like | ChiSq | Pr > ChiSq | Note |
| Parameter list | 1 | 604.70 | 57.64 | <.0001 | MI |
The likelihood ratio test provides a better picture of the significance of the variance component. The difference in the –2 log likelihoods is 57.6, highly significant even if one does not apply the Self and Liang (1987) correction that halves the p-value in this instance.
The results for the 20 most significant estimates are requested with the following statements and shown in Output 41.13.4:
proc sort data=EstStepDownMulti; by Probt; run; proc print data=EstStepDownMulti(obs=20); var Label Estimate StdErr Probt AdjP; run;
The p-values again show the “repeat” pattern corresponding to the monotonicity of the step-down procedure.
Output 41.13.4: The First 20 Estimates in the Ordinal Analysis
| Obs | Label | Estimate | StdErr | Probt | Adjp |
|---|---|---|---|---|---|
| 1 | 37 2 | -2.7224 | 0.8263 | 0.0013 | 0.0133 |
| 2 | 40 2 | -2.8857 | 0.8842 | 0.0015 | 0.0133 |
| 3 | 34 2 | -2.5590 | 0.7976 | 0.0018 | 0.0133 |
| 4 | 43 2 | -3.0491 | 0.9659 | 0.0021 | 0.0133 |
| 5 | 46 2 | -3.2124 | 1.0660 | 0.0032 | 0.0133 |
| 6 | 31 2 | -2.3957 | 0.8010 | 0.0034 | 0.0133 |
| 7 | 49 2 | -3.3758 | 1.1798 | 0.0051 | 0.0164 |
| 8 | 52 2 | -3.5391 | 1.3037 | 0.0077 | 0.0236 |
| 9 | 40 3 | -2.6263 | 0.9718 | 0.0080 | 0.0267 |
| 10 | 37 3 | -2.4630 | 0.9213 | 0.0087 | 0.0267 |
| 11 | 28 2 | -2.2323 | 0.8362 | 0.0088 | 0.0278 |
| 12 | 43 3 | -2.7897 | 1.0451 | 0.0088 | 0.0278 |
| 13 | 46 3 | -2.9530 | 1.1368 | 0.0107 | 0.0291 |
| 14 | 55 2 | -3.7025 | 1.4351 | 0.0112 | 0.0324 |
| 15 | 34 3 | -2.2996 | 0.8974 | 0.0118 | 0.0337 |
| 16 | 49 3 | -3.1164 | 1.2428 | 0.0136 | 0.0344 |
| 17 | 43 1 | -3.3085 | 1.3438 | 0.0154 | 0.0448 |
| 18 | 58 2 | -3.8658 | 1.5722 | 0.0155 | 0.0448 |
| 19 | 40 1 | -3.1451 | 1.2851 | 0.0160 | 0.0448 |
| 20 | 46 1 | -3.4718 | 1.4187 | 0.0160 | 0.0448 |
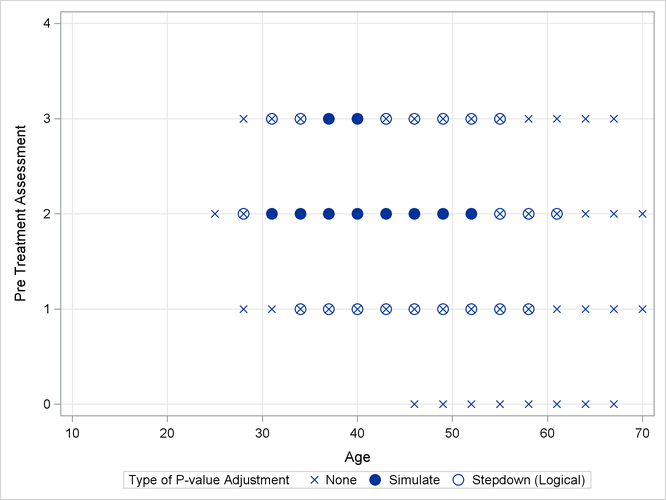
As previously, the comparisons were also performed with standard p-value adjustment via simulation. Output 41.13.5 displays the components of the regressor space in which the response surfaces differ significantly (p < 0.05) between the two treatment arms. As before, the most significant differences occur with unadjusted p-values at the cost of protecting only the individual Type I error rate. The standard multiplicity adjustment has considerably less power than the TCTP adjustment.
Output 41.13.5: Comparison of Significance Regions, Ordinal Analysis