The GLIMMIX Procedure

LSMEANS Statement

LSMEANS fixed-effects </ options> ;

The LSMEANS statement computes least squares means (LS-means) of fixed effects. As in the GLM and the MIXED procedures, LS-means are predicted population margins—that is, they estimate the marginal means over a balanced population. In a sense, LS-means are to unbalanced designs as class and subclass arithmetic means are to balanced designs. The $\mb {L}$ matrix constructed to compute them is the same as the $\mb {L}$ matrix formed in PROC GLM; however, the standard errors are adjusted for the covariance parameters in the model. Least squares means computations are not supported for multinomial models.

Each LS-mean is computed as $\bL \widehat{\bbeta }$ , where $\bL$ is the coefficient matrix associated with the least squares mean and $\widehat{\bbeta }$ is the estimate of the fixed-effects parameter vector. The approximate standard error for the LS-mean is computed as the square root of $\bL \widehat{\mr {Var}}[\widehat{\bbeta }] \bL ’$ . The approximate variance matrix of the fixed-effects estimates depends on the estimation method.

LS-means are constructed on the linked scale—that is, the scale on which the model effects are additive. For example, in a binomial model with logit link, the least squares means are predicted population margins of the logits.

LS-means can be computed for any effect in the MODEL statement that involves only CLASS variables. You can specify multiple effects in one LSMEANS statement or in multiple LSMEANS statements, and all LSMEANS statements must appear after the MODEL statement. As in the ESTIMATE statement, the $\mb {L}$ matrix is tested for estimability, and if this test fails, PROC GLIMMIX displays “Non-est” for the LS-means entries.

Assuming the LS-mean is estimable, PROC GLIMMIX constructs an approximate t test to test the null hypothesis that the associated population quantity equals zero. By default, the denominator degrees of freedom for this test are the same as those displayed for the effect in the “Type III Tests of Fixed Effects” table. If the DDFM=SATTERTHWAITE or DDFM=KENWARDROGER option is specified in the MODEL statement, PROC GLIMMIX determines degrees of freedom separately for each test, unless the DDF= option overrides it for a particular effect. See the DDFM= option for more information. Table 41.8 summarizes options available in the LSMEANS statement. All LSMEANS options are subsequently discussed in alphabetical order.

Table 41.8: LSMEANS Statement Options

Option	Description
Construction and Computation of LS-Means
AT	Modifies covariate value in computing LS-means
BYLEVEL	Computes separate margins
DIFF	Requests differences of LS-means
OM	Specifies weighting scheme for LS-mean computation as determined by the input data set
SINGULAR=	Tunes estimability checking
SLICE=	Partitions F tests (simple effects)
SLICEDIFF=	Requests simple effects differences
SLICEDIFFTYPE	Determines the type of simple difference
Degrees of Freedom and P-values
ADJDFE=	Determines whether to compute row-wise denominator degrees of freedom with DDFM=SATTERTHWAITE or DDFM=KENWARDROGER
ADJUST=	Determines the method for multiple comparison adjustment of LS-mean differences
ALPHA= $\alpha$	Determines the confidence level ( $1-\alpha$ )
DF=	Assigns specific value to degrees of freedom for tests and confidence limits
STEPDOWN	Adjusts multiple comparison p-values further in a step-down fashion
Statistical Output
CL	Constructs confidence limits for means and or mean differences
CORR	Displays correlation matrix of LS-means
COV	Displays covariance matrix of LS-means
E	Prints the $\mb {L}$ matrix
ILINK	Applies the inverse link transform to the LS-Means (not differences) and produces the standard errors on the inverse linked scale
LINES	Produces “Lines” display for pairwise LS-mean differences
ODDS	Reports odds of levels of fixed effects if permissible by the link function
ODDSRATIO	Reports (simple) differences of least squares means in terms of odds ratios if permissible by the link function
PLOTS=	Requests ODS statistical graphics of means and mean comparisons

You can specify the following options in the LSMEANS statement after a slash (/).

ADJDFE=ROW ADJDFE=SOURCE

specifies how denominator degrees of freedom are determined when p-values and confidence limits are adjusted for multiple comparisons with the ADJUST= option. When you do not specify the ADJDFE= option, or when you specify ADJDFE=SOURCE, the denominator degrees of freedom for multiplicity-adjusted results are the denominator degrees of freedom for the LS-mean effect in the “Type III Tests of Fixed Effects” table. When you specify ADJDFE=ROW, the denominator degrees of freedom for multiplicity-adjusted results correspond to the degrees of freedom displayed in the DF column of the “Differences of Least Squares Means” table.

The ADJDFE=ROW setting is particularly useful if you want multiplicity adjustments to take into account that denominator degrees of freedom are not constant across LS-mean differences. This can be the case, for example, when the DDFM=SATTERTHWAITE or DDFM=KENWARDROGER degrees-of-freedom method is in effect.

In one-way models with heterogeneous variance, combining certain ADJUST= options with the ADJDFE=ROW option corresponds to particular methods of performing multiplicity adjustments in the presence of heteroscedasticity. For example, the following statements fit a heteroscedastic one-way model and perform Dunnett’s T3 method (Dunnett, 1980), which is based on the studentized maximum modulus (ADJUST=SMM):

proc glimmix;
   class A;
   model y = A / ddfm=satterth;
   random _residual_ / group=A;
   lsmeans A / adjust=smm adjdfe=row;
run;

If you combine the ADJDFE=ROW option with ADJUST=SIDAK, the multiplicity adjustment corresponds to the T2 method of Tamhane (1979), while ADJUST=TUKEY corresponds to the method of Games-Howell (Games and Howell, 1976). Note that ADJUST=TUKEY gives the exact results for the case of fractional degrees of freedom in the one-way model, but it does not take into account that the degrees of freedom are subject to variability. A more conservative method, such as ADJUST=SMM, might protect the overall error rate better.

Unless the ADJUST= option is specified in the LSMEANS statement, the ADJDFE= option has no effect.

ADJUST=BON ADJUST=DUNNETT ADJUST=NELSON ADJUST=SCHEFFE ADJUST=SIDAK ADJUST=SIMULATE<(simoptions)> ADJUST=SMM | GT2 ADJUST=TUKEY

requests a multiple comparison adjustment for the p-values and confidence limits for the differences of LS-means. The adjusted quantities are produced in addition to the unadjusted quantities. By default, PROC GLIMMIX performs all pairwise differences. If you specify ADJUST=DUNNETT, the procedure analyzes all differences with a control level. If you specify ADJUST=NELSON, ANOM differences are taken. The ADJUST= option implies the DIFF option, unless the SLICEDIFF= option is specified.

The BON (Bonferroni) and SIDAK adjustments involve correction factors described in Chapter 42: The GLM Procedure, and Chapter 61: The MULTTEST Procedure; also see Westfall and Young (1993) and Westfall et al. (1999). When you specify ADJUST=TUKEY and your data are unbalanced, PROC GLIMMIX uses the approximation described in Kramer (1956) and identifies the adjustment as “Tukey-Kramer” in the results. Similarly, when you specify ADJUST=DUNNETT or ADJUST=NELSON and the LS-means are correlated, the GLIMMIX procedure uses the factor-analytic covariance approximation described in Hsu (1992) and identifies the adjustment in the results as “Dunnett-Hsu” or “Nelson-Hsu,” respectively. The approximation derives an approximate “effective sample sizes” for which exact critical values are computed. Note that computing the exact adjusted p-values and critical values for unbalanced designs can be computationally intensive, in particular for ADJUST=NELSON. A simulation-based approach, as specified by the ADJUST=SIM option, while nondeterministic, can provide inferences that are sufficiently accurate in much less time. The preceding references also describe the SCHEFFE and SMM adjustments.

Nelson’s adjustment applies only to the analysis of means (Ott, 1967; Nelson, 1982, 1991, 1993), where LS-means are compared against an average LS-mean. It does not apply to all pairwise differences of least squares means, or to slice differences that you specify with the SLICEDIFF= option. See the DIFF=ANOM option for more details regarding the analysis of means with the GLIMMIX procedure.

The SIMULATE adjustment computes adjusted p-values and confidence limits from the simulated distribution of the maximum or maximum absolute value of a multivariate t random vector. All covariance parameters, except the residual scale parameter, are fixed at their estimated values throughout the simulation, potentially resulting in some underdispersion. The simulation estimates q, the true 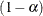$(1-\alpha )$ quantile, where 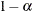$1 - \alpha$ is the confidence coefficient. The default $\alpha$ is 0.05, and you can change this value with the ALPHA= option in the LSMEANS statement.

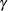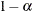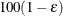The number of samples is set so that the tail area for the simulated q is within $\gamma$ of $1 - \alpha$ with $100(1-\epsilon )$ % confidence. In equation form,

$\mr {Pr}(|F(\widehat{q})-(1-\alpha )| \leq \gamma ) = 1 - \epsilon$

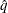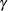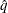where $\hat{q}$ is the simulated q and F is the true distribution function of the maximum; see Edwards and Berry (1987) for details. By default, $\gamma$ = 0.005 and $\epsilon$ = 0.01, placing the tail area of $\hat{q}$ within 0.005 of 0.95 with 99% confidence. The ACC= and EPS= simoptions reset 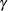$\gamma$ and $\epsilon$ , respectively, the NSAMP= simoption sets the sample size directly, and the SEED= simoption specifies an integer used to start the pseudo-random number generator for the simulation. If you do not specify a seed, or if you specify a value less than or equal to zero, the seed is generated from reading the time of day from the computer clock. For additional descriptions of these and other simulation options, see the section LSMEANS Statement in Chapter 42: The GLM Procedure.

If the STEPDOWN option is in effect, the p-values are further adjusted in a step-down fashion. For certain options and data, this adjustment is exact under an iid 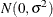$N(0,\sigma ^2)$ model for the dependent variable, in particular for the following:

for ADJUST=DUNNETT when the means are uncorrelated
for ADJUST=TUKEY with STEPDOWN(TYPE=LOGICAL) when the means are balanced and uncorrelated.

The first case is a consequence of the nature of the successive step-down hypotheses for comparisons with a control; the second employs an extension of the maximum studentized range distribution appropriate for partition hypotheses (Royen, 1989). Finally, for STEPDOWN(TYPE=FREE), ADJUST=TUKEY employs the Royen (1989) extension in such a way that the resulting p-values are conservative.

ALPHA=number

requests that a t-type confidence interval be constructed for each of the LS-means with confidence level 1 – number. The value of number must be between 0 and 1; the default is 0.05.

AT variable=value AT (variable-list)=(value-list) AT MEANS

enables you to modify the values of the covariates used in computing LS-means. By default, all covariate effects are set equal to their mean values for computation of standard LS-means. The AT option enables you to assign arbitrary values to the covariates. Additional columns in the output table indicate the values of the covariates.

If there is an effect containing two or more covariates, the AT option sets the effect equal to the product of the individual means rather than the mean of the product (as with standard LS-means calculations). The AT MEANS option sets covariates equal to their mean values (as with standard LS-means) and incorporates this adjustment to crossproducts of covariates.

As an example, consider the following invocation of PROC GLIMMIX:

proc glimmix;
   class A;
   model Y = A x1 x2 x1*x2;
   lsmeans A;
   lsmeans A / at means;
   lsmeans A / at x1=1.2;
   lsmeans A / at (x1 x2)=(1.2 0.3);
run;

For the first two LSMEANS statements, the LS-means coefficient for x1 is 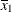$\overline{x}_1$ (the mean of x1) and for x2 is 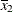$\overline{x}_2$ (the mean of x2). However, for the first LSMEANS statement, the coefficient for x1*x2 is 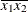$\overline{x_1x_2}$ , but for the second LSMEANS statement, the coefficient is 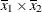$\overline{x}_1\times \overline{x}_2$ . The third LSMEANS statement sets the coefficient for x1 equal to 1.2 and leaves it at 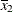$\overline{x}_2$ for x2, and the final LSMEANS statement sets these values to 1.2 and 0.3, respectively.

Even if you specify a WEIGHT variable, the unweighted covariate means are used for the covariate coefficients if there is no AT specification. If you specify the AT option, WEIGHT or FREQ variables are taken into account as follows. The weighted covariate means are then used for the covariate coefficients for which no explicit AT values are given, or if you specify AT MEANS. Observations that do not contribute to the analysis because of a missing dependent variable are included in computing the covariate means. You should use the E option in conjunction with the AT option to check that the modified LS-means coefficients are the ones you want.

The AT option is disabled if you specify the BYLEVEL option.

BYLEVEL

requests that separate margins be computed for each level of the LSMEANS effect.

The standard LS-means have equal coefficients across classification effects. The BYLEVEL option changes these coefficients to be proportional to the observed margins. This adjustment is reasonable when you want your inferences to apply to a population that is not necessarily balanced but has the margins observed in the input data set. In this case, the resulting LS-means are actually equal to raw means for fixed-effects models and certain balanced random-effects models, but their estimated standard errors account for the covariance structure that you have specified. If a WEIGHT statement is specified, PROC GLIMMIX uses weighted margins to construct the LS-means coefficients.

If the AT option is specified, the BYLEVEL option disables it.

CL

requests that t-type confidence limits be constructed for each of the LS-means. If DDFM=NONE, then PROC GLIMMIX uses infinite degrees of freedom for this test, essentially computing a z interval. The confidence level is 0.95 by default; this can be changed with the ALPHA= option. If you specify an ADJUST= option, then the confidence limits are adjusted for multiplicity, but if you also specify STEPDOWN, then only p-values are step-down adjusted, not the confidence limits.

CORR

displays the estimated correlation matrix of the least squares means as part of the “Least Squares Means” table.

COV

displays the estimated covariance matrix of the least squares means as part of the “Least Squares Means” table.

DF=number

specifies the degrees of freedom for the t test and confidence limits. The default is the denominator degrees of freedom taken from the “Type III Tests of Fixed Effects” table corresponding to the LS-means effect.

DIFF<=difftype> PDIFF<=difftype>

requests that differences of the LS-means be displayed. The optional difftype specifies which differences to produce, with possible values ALL, ANOM, CONTROL, CONTROLL, and CONTROLU. The ALL value requests all pairwise differences, and it is the default. The CONTROL difftype requests differences with a control, which, by default, is the first level of each of the specified LSMEANS effects.

The ANOM value requests differences between each LS-mean and the average LS-mean, as in the analysis of means (Ott, 1967). The average is computed as a weighted mean of the LS-means, the weights being inversely proportional to the diagonal entries of the

$\bL \left(\bX ’\bX \right)^{-} \bL ’$

matrix. If LS-means are nonestimable, this design-based weighted mean is replaced with an equally weighted mean. Note that the ANOM procedure in SAS/QC software implements both tables and graphics for the analysis of means with a variety of response types. For one-way designs and normal data with identity link, the DIFF=ANOM computations are equivalent to the results of PROC ANOM. If the LS-means being compared are uncorrelated, exact adjusted p-values and critical values for confidence limits can be computed in the analysis of means; see Nelson (1982, 1991, 1993); Guirguis and Tobias (2004) as well as the documentation for the ADJUST=NELSON option.

To specify which levels of the effects are the controls, list the quoted formatted values in parentheses after the CONTROL keyword. For example, if the effects A, B, and C are classification variables, each having two levels, 1 and 2, the following LSMEANS statement specifies the (1,2) level of A*B and the (2,1) level of B*C as controls:

lsmeans A*B B*C / diff=control('1' '2' '2' '1');

For multiple effects, the results depend upon the order of the list, and so you should check the output to make sure that the controls are correct.

Two-tailed tests and confidence limits are associated with the CONTROL difftype. For one-tailed results, use either the CONTROLL or CONTROLU difftype. The CONTROLL difftype tests whether the noncontrol levels are significantly smaller than the control; the upper confidence limits for the control minus the noncontrol levels are considered to be infinity and are displayed as missing. Conversely, the CONTROLU difftype tests whether the noncontrol levels are significantly larger than the control; the upper confidence limits for the noncontrol levels minus the control are considered to be infinity and are displayed as missing.

If you want to perform multiple comparison adjustments on the differences of LS-means, you must specify the ADJUST= option.

The differences of the LS-means are displayed in a table titled “Differences of Least Squares Means.”

E

requests that the $\mb {L}$ matrix coefficients for the LSMEANS effects be displayed.

ILINK

requests that estimates and their standard errors in the “Least Squares Means” table also be reported on the scale of the mean (the inverse linked scale). The ILINK option is specific to an LSMEANS statement. If you also specify the CL option, the GLIMMIX procedure computes confidence intervals for the predicted means by applying the inverse link transform to the confidence limits on the linked (linear) scale. Standard errors on the inverse linked scale are computed by the delta method.

The GLIMMIX procedure applies the inverse link transform to the LS-mean reported in the Estimate column. In a logistic model, for example, this implies that the value reported as the inversely linked estimate corresponds to a predicted probability that is based on an average estimable function (the estimable function that produces the LS-mean on the linear scale). To compute average predicted probabilities, you can average the results from applying the ILINK option in the ESTIMATE statement for suitably chosen estimable functions.

LINES

presents results of comparisons between all pairs of least squares means by listing the means in descending order and indicating nonsignificant subsets by line segments beside the corresponding LS-means. When all differences have the same variance, these comparison lines are guaranteed to accurately reflect the inferences based on the corresponding tests, made by comparing the respective p-values to the value of the ALPHA= option (0.05 by default). However, equal variances might not be the case for differences between LS-means. If the variances are not all the same, then the comparison lines might be conservative, in the sense that if you base your inferences on the lines alone, you will detect fewer significant differences than the tests indicate. If there are any such differences, PROC GLIMMIX lists the pairs of means that are inferred to be significantly different by the tests but not by the comparison lines. Note, however, that in many cases, even though the variances are unequal, they are similar enough that the comparison lines accurately reflect the test inferences.

ODDS

requests that in models with logit, cumulative logit, and generalized logit link function the odds of the levels of the fixed effects are reported. If you specify the CL or ALPHA= option, confidence intervals for the odds are also computed. See the section Odds and Odds Ratio Estimation for further details about computation and interpretation of odds and odds ratios with the GLIMMIX procedure.

ODDSRATIO OR

requests that LS-mean differences (DIFF, ADJUST= options) and simple effect comparisons (SLICEDIFF option) are also reported in terms of odds ratios. The ODDSRATIO option is ignored unless you use either the logit, cumulative logit, or generalized logit link function. If you specify the CL or ALPHA= option, confidence intervals for the odds ratios are also computed. These intervals are adjusted for multiplicity when you specify the ADJUST= option. See the section Odds and Odds Ratio Estimation for further details about computation and interpretation of odds and odds ratios with the GLIMMIX procedure.

OBSMARGINS OM

specifies a potentially different weighting scheme for the computation of LS-means coefficients. The standard LS-means have equal coefficients across classification effects; however, the OM option changes these coefficients to be proportional to those found in the input data set. This adjustment is reasonable when you want your inferences to apply to a population that is not necessarily balanced but has the margins observed in your data.

In computing the observed margins, PROC GLIMMIX uses all observations for which there are no missing or invalid independent variables, including those for which there are missing dependent variables. Also, if you use a WEIGHT statement, PROC GLIMMIX computes weighted margins to construct the LS-means coefficients. If your data are balanced, the LS-means are unchanged by the OM option.

The BYLEVEL option modifies the observed-margins LS-means. Instead of computing the margins across all of the input data set, PROC GLIMMIX computes separate margins for each level of the LSMEANS effect in question. In this case the resulting LS-means are actually equal to raw means for fixed-effects models and certain balanced random-effects models, but their estimated standard errors account for the covariance structure that you have specified.

You can use the E option in conjunction with either the OM or BYLEVEL option to check that the modified LS-means coefficients are the ones you want. It is possible that the modified LS-means are not estimable when the standard ones are estimable, or vice versa.

PDIFF

is the same as the DIFF option.

PLOT | PLOTS<=plot-request<(options)>> PLOT | PLOTS<=(plot-request<(options)> <…plot-request<(options)> >)>

creates least squares means related graphs when ODS Graphics has been enabled and the plot request does not conflict with other options in the LSMEANS statement. For general information about ODS Graphics, see Chapter 21: Statistical Graphics Using ODS. For examples of the basic statistical graphics for least squares means and aspects of their computation and interpretation, see the section Graphics for LS-Mean Comparisons in this chapter.

The options for a specific plot request (and their suboptions) of the LSMEANS statement include those for the PLOTS= option in the PROC GLIMMIX statement. You can specify classification effects in the MEANPLOT request of the LSMEANS statement to control the display of interaction means with the PLOTBY= and SLICEBY= suboptions; these are not available in the PLOTS= option in the PROC GLIMMIX statement. Options specified in the LSMEANS statement override those in the PLOTS= option in the PROC GLIMMIX statement.

The available options and suboptions are as follows.

ALL

requests that the default plots corresponding to this LSMEANS statement be produced. The default plot depends on the options in the statement.

ANOMPLOT

ANOM

requests an analysis of means display in which least squares means are compared to an average least squares mean. Least squares mean ANOM plots are produced only for those model effects listed in LSMEANS statements that have options that do not contradict with the display. For example, the following statements produce analysis of mean plots for effects A and C:

lsmeans A / diff=anom plot=anom;
lsmeans B / diff      plot=anom;
lsmeans C /           plot=anom;

The DIFF option in the second LSMEANS statement implies all pairwise differences.

CONTROLPLOT

CONTROL

requests a display in which least squares means are visually compared against a reference level. These plots are produced only for statements with options that are compatible with control differences. For example, the following statements produce control plots for effects A and C:

lsmeans A / diff=control('1') plot=control;
lsmeans B / diff              plot=control;
lsmeans C                     plot=control;

The DIFF option in the second LSMEANS statement implies all pairwise differences.

DIFFPLOT<(diffplot-options)>

DIFFOGRAM<(diffplot-options)> DIFF<(diffplot-options)>

requests a display of all pairwise least squares mean differences and their significance. The display is also known as a “mean-mean scatter plot” when it is based on arithmetic means (Hsu, 1996; Hsu and Peruggia, 1994). For each comparison a line segment, centered at the LS-means in the pair, is drawn. The length of the segment corresponds to the projected width of a confidence interval for the least squares mean difference. Segments that fail to cross the 45-degree reference line correspond to significant least squares mean differences.

LS-mean difference plots are produced only for statements with options that are compatible with the display. For example, the following statements request differences against a control level for the A effect, all pairwise differences for the B effect, and the least squares means for the C effect:

lsmeans A / diff=control('1') plot=diff;
lsmeans B / diff              plot=diff;
lsmeans C                     plot=diff;

The DIFF= type in the first statement is incompatible with a display of all pairwise differences.

You can specify the following diffplot-options. The ABS and NOABS options determine the positioning of the line segments in the plot. When the ABS option is in effect, and this is the default, all line segments are shown on the same side of the reference line. The NOABS option separates comparisons according to the sign of the difference. The CENTER option marks the center point for each comparison. This point corresponds to the intersection of two least squares means. The NOLINES option suppresses the display of the line segments that represent the confidence bounds for the differences of the least squares means. The NOLINES option implies the CENTER option. The default is to draw line segments in the upper portion of the plot area without marking the center point.

MEANPLOT<(meanplot-options)>

requests displays of the least squares means.

The following meanplot-options control the display of the least squares means.

ASCENDING

displays the least squares means in ascending order. This option has no effect if means are sliced or displayed in separate plots.

CL

displays upper and lower confidence limits for the least squares means. By default, 95% limits are drawn. You can change the confidence level with the ALPHA= option. Confidence limits are drawn by default if the CL option is specified in the LSMEANS statement.

CLBAND

displays confidence limits as bands. This option implies the JOIN option.

DESCENDING

displays the least squares means in descending order. This option has no effect if means are sliced or displayed in separate plots.

ILINK

requests that means (and confidence limits) are displayed on the inverse linked scale.

JOIN CONNECT

connects the least squares means with lines. This option is implied by the CLBAND option. If the effect contains nested variables, and a SLICEBY= effect contains classification variables that appear as crossed effects, this option is ignored.

SLICEBY=fixed-effect

specifies an effect by which to group the means in a single plot. For example, the following statement requests a plot in which the levels of A are placed on the horizontal axis and the means that belong to the same level of B are joined by lines:

lsmeans A*B / plot=meanplot(sliceby=b join);

Unless the LS-mean effect contains at least two classification variables, the SLICEBY= option has no effect. The fixed-effect does not have to be an effect in your MODEL statement, but it must consist entirely of classification variables.

PLOTBY=fixed-effect

specifies an effect by which to break interaction plots into separate displays. For example, the following statement requests for each level of C one plot of the A*B cell means that are associated with that level of C:

lsmeans A*B*C / plot=meanplot(sliceby=b plotby=c clband);

In each plot, levels of A are displayed on the horizontal axis, and confidence bands are drawn around the means that share the same level of B.

The PLOTBY= option has no effect unless the LS-mean effect contains at least three classification variables. The fixed-effect does not have to be an effect in the MODEL statement, but it must consist entirely of classification variables.

NONE

requests that no plots be produced.

When LS-mean calculations are adjusted for multiplicity by using the ADJUST= option, the plots are adjusted accordingly.

SINGULAR=number

tunes the estimability checking as documented for the CONTRAST statement.

SLICE=fixed-effect SLICE=(fixed-effects)

specifies effects by which to partition interaction LSMEANS effects. This can produce what are known as tests of simple effects (Winer, 1971). For example, suppose that A*B is significant, and you want to test the effect of A for each level of B. The appropriate LSMEANS statement is

lsmeans A*B / slice=B;

This statement tests for the simple main effects of A for B, which are calculated by extracting the appropriate rows from the coefficient matrix for the A*B LS-means and by using them to form an F test.

The SLICE option produces F tests that test the simultaneous equality of cell means at a fixed level of the slice effect (Schabenberger, Gregoire, and Kong, 2000). You can request differences of the least squares means while holding one or more factors at a fixed level with the SLICEDIFF= option.

The SLICE option produces a table titled “Tests of Effect Slices.”

SLICEDIFF=fixed-effect SLICEDIFF=(fixed-effects) SIMPLEDIFF=fixed-effect SIMPLEDIFF=(fixed-effects)

requests that differences of simple effects be constructed and tested against zero. Whereas the SLICE option extracts multiple rows of the coefficient matrix and forms an F test, the SLICEDIFF option tests pairwise differences of these rows. This enables you to perform multiple comparisons among the levels of one factor at a fixed level of the other factor. For example, assume that, in a balanced design, factors A and B have a = 4 and b = 3 levels, respectively. Consider the following statements:

proc glimmix;
   class a b;
   model y = a b a*b;
   lsmeans a*b / slice=a;
   lsmeans a*b / slicediff=a;
run;

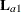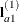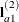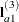The first LSMEANS statement produces four F tests, one per level of A. The first of these tests is constructed by extracting the three rows corresponding to the first level of A from the coefficient matrix for the A*B interaction. Call this matrix $\mb {L}_{a1}$ and its rows $\mb {l}^{(1)}_{a1}$ , $\mb {l}^{(2)}_{a1}$ , and $\mb {l}^{(3)}_{a1}$ . The SLICE tests the two-degrees-of-freedom hypothesis

$H\colon \left\{ \begin{array}{c} \left( \mb {l}^{(1)}_{a1} - \mb {l}^{(2)}_{a1}\right) \bbeta = 0 \\ \left( \mb {l}^{(1)}_{a1} - \mb {l}^{(3)}_{a1}\right) \bbeta = 0 \end{array} \right.$

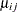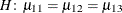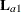In a balanced design, where $\mu _{ij}$ denotes the mean response if A is at level i and B is at level j, this hypothesis is equivalent to $H\colon \mu _{11} = \mu _{12} = \mu _{13}$ . The SLICEDIFF option considers the three rows of $\mb {L}_{a1}$ in turn and performs tests of the difference between pairs of rows. How these differences are constructed depends on the SLICEDIFFTYPE= option. By default, all pairwise differences within the subset of $\mb {L}$ are considered; in the example this corresponds to tests of the form

$\displaystyle H\colon \left(\mb {l}^{(1)}_{a1} - \mb {l}^{(2)}_{a1}\right) \bbeta$	$\displaystyle = 0$
$\displaystyle H\colon \left(\mb {l}^{(1)}_{a1} - \mb {l}^{(3)}_{a1}\right) \bbeta$	$\displaystyle = 0$
$\displaystyle H\colon \left(\mb {l}^{(2)}_{a1} - \mb {l}^{(3)}_{a1}\right) \bbeta$	$\displaystyle = 0$

In the example, with a = 4 and b = 3, the second LSMEANS statement produces four sets of least squares means differences. Within each set, factor A is held fixed at a particular level and each set consists of three comparisons.

When the ADJUST= option is specified, the GLIMMIX procedure also adjusts the tests for multiplicity. The adjustment is based on the number of comparisons within each level of the SLICEDIFF= effect; see the SLICEDIFFTYPE= option. The Nelson adjustment is not available for slice differences.

SLICEDIFFTYPE<=difftype> SIMPLEDIFFTYPE<=difftype>

determines the type of simple effect differences produced with the SLICEDIFF= option.

The possible values for the difftype are ALL, CONTROL, CONTROLL, and CONTROLU. The difftype ALL requests all simple effects differences, and it is the default. The difftype CONTROL requests the differences with a control, which, by default, is the first level of each of the specified LSMEANS effects.

To specify which levels of the effects are the controls, list the quoted formatted values in parentheses after the keyword CONTROL. For example, if the effects A, B, and C are classification variables, each having three levels (1, 2, and 3), the following LSMEANS statement specifies the (1,3) level of A*B as the control:

lsmeans A*B / slicediff=(A B)
              slicedifftype=control('1' '3');

This LSMEANS statement first produces simple effects differences holding the levels of A fixed, and then it produces simple effects differences holding the levels of B fixed. In the former case, level ’3’ of B serves as the control level. In the latter case, level ’1’ of A serves as the control.

For multiple effects, the results depend upon the order of the list, and so you should check the output to make sure that the controls are correct.

STEPDOWN<(step-down options)>

requests that multiple comparison adjustments for the p-values of LS-mean differences be further adjusted in a step-down fashion. Step-down methods increase the power of multiple comparisons by taking advantage of the fact that a p-value will never be declared significant unless all smaller p-values are also declared significant. Note that the STEPDOWN adjustment combined with ADJUST=BON corresponds to the methods of Holm (1979) and “Method 2” of Shaffer (1986); this is the default. Using step-down-adjusted p-values combined with ADJUST=SIMULATE corresponds to the method of Westfall (1997).

If the degrees-of-freedom method is DDFM=KENWARDROGER or DDFM=SATTERTHWAITE, then step-down-adjusted p-values are produced only if the ADJDFE=ROW option is in effect.

Also, STEPDOWN affects only p-values, not confidence limits. For ADJUST=SIMULATE, the generalized least squares hybrid approach of Westfall (1997) is employed to increase Monte Carlo accuracy.

You can specify the following step-down options in parentheses:

MAXTIME=n

specifies the time (in seconds) to spend computing the maximal logically consistent sequential subsets of equality hypotheses for TYPE=LOGICAL. The default is MAXTIME=60. If the MAXTIME value is exceeded, the adjusted tests are not computed. When this occurs, you can try increasing the MAXTIME value. However, note that there are common multiple comparisons problems for which this computation requires a huge amount of time—for example, all pairwise comparisons between more than 10 groups. In such cases, try to use TYPE=FREE (the default) or TYPE=LOGICAL(n) for small n.

REPORT

specifies that a report on the step-down adjustment should be displayed, including a listing of the sequential subsets (Westfall, 1997) and, for ADJUST=SIMULATE, the step-down simulation results.

TYPE=LOGICAL<(n)> TYPE=FREE

If you specify TYPE=LOGICAL, the step-down adjustments are computed by using maximal logically consistent sequential subsets of equality hypotheses (Shaffer, 1986; Westfall, 1997). Alternatively, for TYPE=FREE, sequential subsets are computed ignoring logical constraints. The TYPE=FREE results are more conservative than those for TYPE=LOGICAL, but they can be much more efficient to produce for many comparisons. For example, it is not feasible to take logical constraints between all pairwise comparisons of more than 10 groups. For this reason, TYPE=FREE is the default.

However, you can reduce the computational complexity of taking logical constraints into account by limiting the depth of the search tree used to compute them, specifying the optional depth parameter as a number n in parentheses after TYPE=LOGICAL. As with TYPE=FREE, results for TYPE=LOGICAL(n) are conservative relative to the true TYPE=LOGICAL results, but even for TYPE=LOGICAL(0) they can be appreciably less conservative than TYPE=FREE and they are computationally feasible for much larger numbers of comparisons. If you do not specify n or if n = –1, the full search tree is used.