Bayesian Analysis :: SAS/STAT(R) 12.1 User's Guide

Gibbs Sampling

This section provides details about Bayesian analysis by Gibbs sampling in the location-scale models for survival data available in PROC LIFEREG. See the section Gibbs Sampler for a general discussion of Gibbs sampling. PROC LIFEREG fits parametric location-scale survival models. That is, the probability density of the response Y can expressed in the general form

$f(y) = g\left(\frac{y-\mu }{\sigma }\right)$

where $Y=\log (T)$ for lifetimes T. The function g determines the specific distribution. The location parameter $\mu _ i$ is modeled through regression parameters as $\mu _ i=\mb {x}_ i^\prime \bbeta$ . The LIFEREG procedure can provide Bayesian estimates of the regression parameters and $\sigma$ . The OUTPUT and PROBPLOT statements, if specified, are ignored. The PLOTS=PROBPLOT option in the PROC LIFEREG statement and the CORRB and COVB options in the MODEL statement are also ignored.

For the Weibull distribution, you can specify that Gibbs sampling be performed on the Weibull shape parameter $\beta =\sigma ^{-1}$ instead of the scale parameter $\sigma$ by specifying a prior distribution for the shape parameter with the WEIBULLSHAPEPRIOR= option. In addition, if there are no covariates in the model, you can specify Gibbs sampling on the Weibull scale parameter $\alpha =\exp (\mu )$ , where $\mu$ is the intercept term, with the WEIBULLSCALEPRIOR= option.

In the case of the exponential distribution with no covariates, you can specify Gibbs sampling on the exponential scale parameter $\alpha =\exp (\mu )$ , where $\mu$ is the intercept term, with the EXPSCALEPRIOR= option.

Let $\btheta = (\theta _1, \ldots , \theta _ k)\prime$ be the parameter vector. For location-scale models, the $\theta _ i$ ’s are the regression coefficients $\beta _ i$ ’s and the scale parameter $\sigma$ . In the case of the three-parameter gamma distribution, there is an additional gamma shape parameter $\tau$ . Let $L(D|\btheta )$ be the likelihood function, where D is the observed data. Let $\pi (\btheta )$ be the prior distribution. The full conditional distribution of $[\theta _ i | \theta _ j, i\neq j]$ is proportional to the joint distribution; that is,

$\pi (\theta _ i | \theta _ j, i \neq j, D) \propto L(D|\btheta ) p(\btheta )$

For instance, the one-dimensional conditional distribution of $\theta _1$ given $\theta _ j=\theta _ j^*, 2\leq j \leq k$ , is computed as

$\pi (\theta _1 | \theta _ j=\theta _ j^*, 2\leq j \leq k, D) = L(D|(\btheta =(\theta _1, \theta ^*_2,\ldots ,\theta ^*_ k)’) p(\btheta =(\theta _1, \theta ^*_2,\ldots ,\theta ^*_ k)’)$

Suppose you have a set of arbitrary starting values $\{ \theta _1^{(0)}, \ldots , \theta _ k^{(0)}\}$ . Using the ARMS (adaptive rejection Metropolis sampling) algorithm of Gilks and Wild (1992) and Gilks, Best, and Tan (1995), you can do the following:

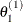draw $\theta _1^{(1)}$ from $[\theta _1|\theta _2^{(0)},\ldots ,\theta _ k^{(0)}]$
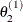draw $\theta _2^{(1)}$ from $[\theta _2|\theta _1^{(1)}, \theta _3^{(0)},\ldots ,\theta _ k^{(0)}]$
$\ldots$
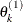draw $\theta _ k^{(1)}$ from $[\theta _ k|\theta _1^{(1)},\ldots ,\theta _{k-1}^{(1)}]$

This completes one iteration of the Gibbs sampler. After one iteration, you have $\{ \theta _1^{(1)}, \ldots , \theta _ k^{(1)}\}$ . After n iterations, you have $\{ \theta _1^{(n)}, \ldots , \theta _ k^{(n)}\}$ . PROC LIFEREG implements the ARMS algorithm based on a program provided by Gilks (2003) to draw a sample from a full conditional distribution. See the section Assessing Markov Chain Convergence for information about assessing the convergence of the chain of posterior samples.

You can output these posterior samples into a SAS data set. The following option in the BAYES statement outputs the posterior samples into the SAS data set Post: OUTPOST=Post. The data set also includes the variables LogPost and LogLike, which represent the log of the posterior distribution and the log of the likelihood, respectively.

Priors for Model Parameters

The model parameters are the regression coefficients and the dispersion parameter (or the precision or scale), if the model has one. The priors for the dispersion parameter and the priors for the regression coefficients are assumed to be independent, while you can have a joint multivariate normal prior for the regression coefficients.

Scale and Shape Parameters

Gamma Prior

The gamma distribution has a PDF

$f_{a,b}(u) = \frac{b (b u)^{a-1}\mr {e}^{-b u}}{\Gamma (a)}, \hspace{1cm} u>0$

where a is the shape parameter and b is the inverse-scale parameter. The mean is $\frac{a}{b}$ and the variance is $\frac{a}{b^2}$ .

Improper Prior

The joint prior density is given by

$p(u) \propto u^{-1}, \hspace{1cm} u>0$

Regression Coefficients

Let $\bbeta$ be the regression coefficients.

Normal Prior

Assume $\bbeta$ has a multivariate normal prior with mean vector $\bbeta _0$ and covariance matrix $\bSigma _0$ . The joint prior density is given by

$p(\bbeta ) \propto \mr {e}^{-\frac{1}{2} (\bbeta -\bbeta _0)^\prime \bSigma _0^{-1}(\bbeta -\bbeta _0)}$

Uniform Prior

The joint prior density is given by

$p(\bbeta ) \propto 1$

Posterior Distribution

Denote the observed data by D.

The posterior distribution is

$\pi (\btheta |D) \propto L_ P(D|\btheta ) p(\btheta )$

where $L_ P(D|\btheta )$ is the likelihood function with regression coefficients and any additional parameters, such as scale or shape, $\btheta$ as parameters; and $p(\btheta )$ is the joint prior distribution of the parameters.

Deviance Information Criterion

Let $\btheta _ i$ be the model parameters at iteration i of the Gibbs sampler, and let LL( $\btheta _ i$ ) be the corresponding model log likelihood. PROC LIFEREG computes the following fit statistics defined by Spiegelhalter et al. (2002):

effective number of parameters:

$p_ D=\overline{\mr {LL}(\btheta )} - \mr {LL}(\bar{\btheta })$

deviance information criterion (DIC):

$\mr {DIC}= \overline{\mr {LL}(\btheta )} + p_ D$

where

$\overline{\mr {LL}(\btheta )} = \frac{1}{n}\sum _{i=1}^ n\mr {LL}(\btheta _ i)$

$\bar{\btheta } = \frac{1}{n}\sum _{i=1}^ n\btheta _ i$

and n is the number of Gibbs samples.

Starting Values of the Markov Chains

When the BAYES statement is specified, PROC LIFEREG generates one Markov chain containing the approximate posterior samples of the model parameters. Additional chains are produced when the Gelman-Rubin diagnostics are requested. Starting values (or initial values) can be specified in the INITIAL= data set in the BAYES statement. If INITIAL= option is not specified, PROC LIFEREG picks its own initial values for the chains.

Denote as the integral value of x. Denote $\hat{s}(X)$ as the estimated standard error of the estimator X.

Regression Coefficients and Gamma Shape Parameter

For the first chain that the summary statistics and regression diagnostics are based on, the default initial values are estimates of the mode of the posterior distribution. If the INITIALMLE option is specified, the initial values are the maximum likelihood estimates; that is,

$\beta _ i^{(0)} = \hat{\beta }_ i$

Initial values for the rth chain ( $r \geq 2$ ) are given by

$\beta _ i^{(0)} = \hat{\beta }_ i \pm \biggl (2+ \biggl [\frac{r}{2} \biggr ] \biggr ) \hat{s}(\hat{\beta }_ i)$

with the plus sign for odd r and minus sign for even r.

Scale, Exponential Scale, Weibull Scale, or Weibull Shape Parameter 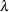$\lambda$

Let $\lambda$ be the parameter sampled.

For the first chain that the summary statistics and diagnostics are based on, the initial values are estimates of the mode of the posterior distribution; or the maximum likelihood estimates if the INITIALMLE option is specified; that is,

$\lambda ^{(0)} = \hat{\lambda }$

The initial values of the rth chain ( $r \geq 2$ ) are given by

$\lambda ^{(0)} = \hat{\lambda } \mr {e}^{\pm \biggl ([\frac{r}{2}]+2 \biggl ) \hat{s}(\hat{\lambda })}$

with the plus sign for odd r and minus sign for even r.

OUTPOST= Output Data Set

The OUTPOST= data set contains the generated posterior samples. There are 2+n variables, where n is the number of model parameters. The variable Iteration represents the iteration number and the variable LogPost contains the log posterior likelihood values. The other n variables represent the draws of the Markov chain for the model parameters.

The LIFEREG Procedure