The LIFEREG Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesModel SpecificationComputational MethodSupported DistributionsPredicted ValuesConfidence IntervalsFit StatisticsProbability PlottingINEST= Data SetOUTEST= Data SetXDATA= Data SetComputational ResourcesBayesian AnalysisDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisODS Table NamesODS Graphics
Missing ValuesModel SpecificationComputational MethodSupported DistributionsPredicted ValuesConfidence IntervalsFit StatisticsProbability PlottingINEST= Data SetOUTEST= Data SetXDATA= Data SetComputational ResourcesBayesian AnalysisDisplayed Output for Classical AnalysisDisplayed Output for Bayesian AnalysisODS Table NamesODS Graphics -
Examples
 Motorette FailureComputing Predicted Values for a Tobit ModelOvercoming Convergence Problems by Specifying Initial ValuesAnalysis of Arbitrarily Censored Data with Interaction EffectsProbability Plotting—Right CensoringProbability Plotting—Arbitrary CensoringBayesian Analysis of Clinical Trial DataModel Postfitting Analysis
Motorette FailureComputing Predicted Values for a Tobit ModelOvercoming Convergence Problems by Specifying Initial ValuesAnalysis of Arbitrarily Censored Data with Interaction EffectsProbability Plotting—Right CensoringProbability Plotting—Arbitrary CensoringBayesian Analysis of Clinical Trial DataModel Postfitting Analysis - References
Example 51.6 Probability Plotting—Arbitrary Censoring
Table 51.16 contains microprocessor failure data (Nelson, 1990). Units were inspected at predetermined time intervals. The data consist of inspection interval endpoints (in hours) and the number of units failing in each interval. A missing (.) lower endpoint indicates left censoring, and a missing upper endpoint indicates right censoring. These can be thought of as semi-infinite intervals with a lower (upper) endpoint of negative (positive) infinity for left (right) censoring.
Table 51.16: Interval-Censored Data
|
Lower Endpoint |
Upper Endpoint |
Number Failed |
|---|---|---|
|
. |
6 |
6 |
|
6 |
12 |
2 |
|
24 |
48 |
2 |
|
24 |
. |
1 |
|
48 |
168 |
1 |
|
48 |
. |
839 |
|
168 |
500 |
1 |
|
168 |
. |
150 |
|
500 |
1000 |
2 |
|
500 |
. |
149 |
|
1000 |
2000 |
1 |
|
1000 |
. |
147 |
|
2000 |
. |
122 |
The following SAS statements create the SAS data set Micro:
data Micro; input t1 t2 f; datalines; . 6 6 6 12 2 12 24 0 24 48 2 24 . 1 48 168 1 48 . 839 168 500 1 168 . 150 500 1000 2 500 . 149 1000 2000 1 1000 . 147 2000 . 122 ;
The following SAS statements compute the nonparametric Turnbull estimate of the cumulative distribution function and create a lognormal probability plot:
ods graphics on; proc lifereg data=Micro; model ( t1 t2 ) = / d=lognormal intercept=25 scale=5; weight f; probplot pupper = 10 itprintem printprobs maxitem = (1000,25) ppout; inset; run; ods graphics off;
The two initial values INTERCEPT=25 and SCALE=5 in the MODEL statement are used to aid convergence in the model-fitting algorithm.
The following tables are created by the PROBPLOT statement in addition to the standard tabular output from the MODEL statement. Output 51.6.1 shows the iteration history for the Turnbull estimate of the CDF for the microprocessor data. With both options ITPRINTEM and PRINTPROBS specified in the PROBPLOT statement, this table contains the log likelihoods and interval probabilities for every 25th iteration and the last iteration. It would contain only the log likelihoods if the option PRINTPROBS were not specified.
Output 51.6.1: Iteration History for the Turnbull Estimate
| Iteration History for the Turnbull Estimate of the CDF | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Iteration | Loglikelihood | (., 6) | (6, 12) | (24, 48) | (48, 168) | (168, 500) | (500, 1000) | (1000, 2000) | (2000, .) |
| 0 | -1133.4051 | 0.125 | 0.125 | 0.125 | 0.125 | 0.125 | 0.125 | 0.125 | 0.125 |
| 25 | -104.16622 | 0.00421644 | 0.00140548 | 0.00140648 | 0.00173338 | 0.00237846 | 0.00846094 | 0.04565407 | 0.93474475 |
| 50 | -101.15151 | 0.00421644 | 0.00140548 | 0.00140648 | 0.00173293 | 0.00234891 | 0.00727679 | 0.01174486 | 0.96986811 |
| 75 | -101.06641 | 0.00421644 | 0.00140548 | 0.00140648 | 0.00173293 | 0.00234891 | 0.00727127 | 0.00835638 | 0.9732621 |
| 100 | -101.06534 | 0.00421644 | 0.00140548 | 0.00140648 | 0.00173293 | 0.00234891 | 0.00727125 | 0.00801814 | 0.97360037 |
| 125 | -101.06533 | 0.00421644 | 0.00140548 | 0.00140648 | 0.00173293 | 0.00234891 | 0.00727125 | 0.00798438 | 0.97363413 |
| 130 | -101.06533 | 0.00421644 | 0.00140548 | 0.00140648 | 0.00173293 | 0.00234891 | 0.00727125 | 0.007983 | 0.97363551 |
The table in Output 51.6.2 summarizes the Turnbull estimates of the interval probabilities, the reduced gradients, and Lagrange multipliers as described in the section Arbitrarily Censored Data.
Output 51.6.2: Summary for the Turnbull Algorithm
| Lower Lifetime | Upper Lifetime | Probability | Reduced Gradient | Lagrange Multiplier |
|---|---|---|---|---|
| . | 6 | 0.0042 | 0 | 0 |
| 6 | 12 | 0.0014 | 0 | 0 |
| 24 | 48 | 0.0014 | 0 | 0 |
| 48 | 168 | 0.0017 | 0 | 0 |
| 168 | 500 | 0.0023 | 0 | 0 |
| 500 | 1000 | 0.0073 | -7.219342E-9 | 0 |
| 1000 | 2000 | 0.0080 | -0.037063236 | 0 |
| 2000 | . | 0.9736 | 0.0003038877 | 0 |
Output 51.6.3 shows the final estimate of the CDF, along with standard errors and nonparametric confidence limits. Two kinds of nonparametric confidence limits, pointwise or simultaneous, are available. The default is the pointwise nonparametric confidence limits. You can specify the simultaneous nonparametric confidence limits by using the NPINTERVALS=SIMUL option.
Output 51.6.3: Final CDF Estimates for Turnbull Algorithm
| Cumulative Probability Estimates | |||||
|---|---|---|---|---|---|
| Lower Lifetime | Upper Lifetime | Cumulative Probability |
Pointwise 95% Confidence Limits |
Standard Error | |
| Lower | Upper | ||||
| 6 | 6 | 0.0042 | 0.0019 | 0.0094 | 0.0017 |
| 12 | 24 | 0.0056 | 0.0028 | 0.0112 | 0.0020 |
| 48 | 48 | 0.0070 | 0.0038 | 0.0130 | 0.0022 |
| 168 | 168 | 0.0088 | 0.0047 | 0.0164 | 0.0028 |
| 500 | 500 | 0.0111 | 0.0058 | 0.0211 | 0.0037 |
| 1000 | 1000 | 0.0184 | 0.0094 | 0.0357 | 0.0063 |
| 2000 | 2000 | 0.0264 | 0.0124 | 0.0553 | 0.0101 |
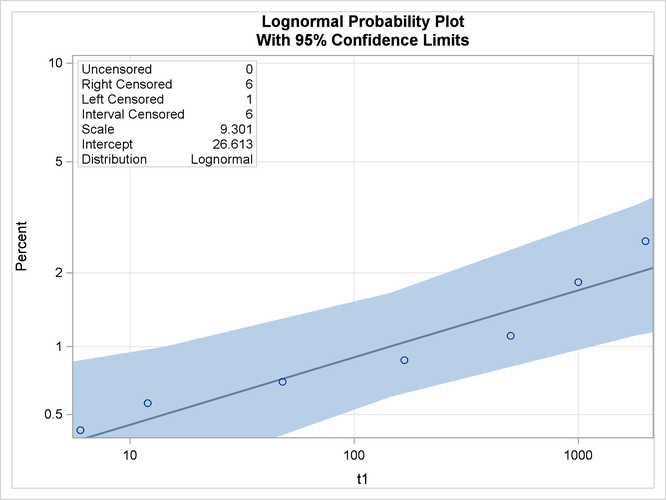
Output 51.6.4 shows the CDF estimates, maximum likelihood fit, and pointwise parametric confidence limits plotted on a lognormal probability plot.
Output 51.6.4: Lognormal Probability Plot for the Microprocessor Data