The NLMIXED Procedure

Finite-Difference Approximations of Derivatives

Forward-Difference Approximations
Central-Difference Approximations

The FD= and FDHESSIAN= options specify the use of finite-difference approximations of the derivatives. The FD= option specifies that all derivatives are approximated using function evaluations, and the FDHESSIAN= option specifies that second-order derivatives are approximated using gradient evaluations.

Computing derivatives by finite-difference approximations can be very time-consuming, especially for second-order derivatives based only on values of the objective function (FD= option). If analytical derivatives are difficult to obtain (for example, if a function is computed by an iterative process), you might consider one of the optimization techniques that use first-order derivatives only (QUANEW, DBLDOG, or CONGRA). In the expressions that follow, $\btheta$ denotes the parameter vector, denotes the step size for the ith parameter, and $\mb {e}_ i$ is a vector of zeros with a 1 in the ith position.

Forward-Difference Approximations

The forward-difference derivative approximations consume less computer time, but they are usually not as precise as approximations that use central-difference formulas.

For first-order derivatives, n additional function calls are required:

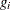
$\displaystyle g_ i$

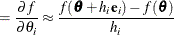
$\displaystyle = \frac{\partial f}{\partial \theta _ i} \approx \frac{f(\btheta + h_ i\mb {e}_ i) - f(\btheta )}{h_ i}$

For second-order derivatives based on function calls only (Dennis and Schnabel, 1983, p. 80), 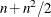additional function calls are required for dense Hessian:

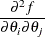
$\displaystyle \frac{\partial ^2 f}{\partial \theta _ i \partial \theta _ j}$

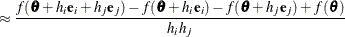
$\displaystyle \approx \frac{f(\btheta +h_ i\mb {e}_ i+h_ j\mb {e}_ j) - f(\btheta +h_ i\mb {e}_ i) - f(\btheta +h_ j\mb {e}_ j) + f(\btheta )}{h_ i h_ j}$

For second-order derivatives based on gradient calls (Dennis and Schnabel, 1983, p. 103), n additional gradient calls are required:

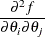
$\displaystyle \frac{\partial ^2 f}{\partial \theta _ i \partial \theta _ j}$

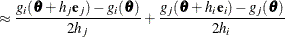
$\displaystyle \approx \frac{g_ i(\btheta + h_ j\mb {e}_ j) - g_ i(\btheta )}{2h_ j} + \frac{g_ j(\btheta + h_ i\mb {e}_ i) - g_ j(\btheta )}{2h_ i}$

Central-Difference Approximations

Central-difference approximations are usually more precise, but they consume more computer time than approximations that use forward-difference derivative formulas.

For first-order derivatives, 2n additional function calls are required:

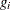
$\displaystyle g_ i$

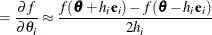
$\displaystyle = \frac{\partial f}{\partial \theta _ i} \approx \frac{f(\btheta + h_ i\mb {e}_ i) - f(\btheta - h_ i\mb {e}_ i)}{2h_ i}$

For second-order derivatives based on function calls only (Abramowitz and Stegun, 1972, p. 884), 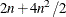additional function calls are required.

$\displaystyle \frac{\partial ^2 f}{\partial \theta ^2_ i}$

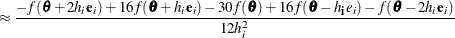
$\displaystyle \approx \frac{-f(\btheta + 2h_ i\mb {e}_ i) + 16f(\btheta + h_ i\mb {e}_ i) - 30f(\btheta ) + 16f(\btheta - h_\mb {i}e_ i) - f(\btheta - 2h_ i\mb {e}_ i)}{12h^2_ i}$

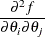
$\displaystyle \frac{\partial ^2 f}{\partial \theta _ i \partial \theta _ j}$

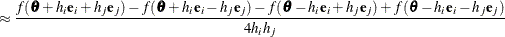
$\displaystyle \approx \frac{f(\btheta +h_ i\mb {e}_ i+h_ j\mb {e}_ j) - f(\btheta +h_ i\mb {e}_ i-h_ j\mb {e}_ j) - f(\btheta -h_ i\mb {e}_ i+h_ j\mb {e}_ j) + f(\btheta -h_ i\mb {e}_ i-h_ j\mb {e}_ j)}{4h_ ih_ j} \nonumber$

For second-order derivatives based on gradient calls, 2n additional gradient calls are required:

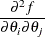
$\displaystyle \frac{\partial ^2 f}{\partial \theta _ i \partial \theta _ j}$

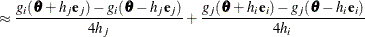
$\displaystyle \approx \frac{g_ i(\btheta + h_ j\mb {e}_ j) - g_ i(\btheta - h_ j\mb {e}_ j)}{4h_ j} + \frac{g_ j(\btheta + h_ i\mb {e}_ i) - g_ j(\btheta - h_ i\mb {e}_ i)}{4h_ i}$

You can use the FDIGITS= option to specify the number of accurate digits in the evaluation of the objective function. This specification is helpful in determining an appropriate interval size h to be used in the finite-difference formulas.

The step sizes , $j=1,\ldots ,n$ are defined as follows:

For the forward-difference approximation of first-order derivatives that use function calls and second-order derivatives that use gradient calls, $h_ j = \sqrt [2]{\eta } (1 + |\theta _ j|)$ .
For the forward-difference approximation of second-order derivatives that use only function calls and all central-difference formulas, $h_ j = \sqrt [3]{\eta } (1 + |\theta _ j|)$ .

The value of $\eta$ is defined by the FDIGITS= option:

If you specify the number of accurate digits by using FDIGITS=r, $\eta$ is set to $10^{-r}$ .
If you do not specify the FDIGITS= option, $\eta$ is set to the machine precision $\epsilon$ .