The NLMIXED Procedure

Abramowitz, M. and Stegun, I. A. (1972), Handbook of Mathematical Functions, New York: Dover Publications.

Anderson, D. A. and Aitkin, M. (1985), “Variance Component Models with Binary Response: Interviewer Variability,” Journal of the Royal Statistical Society, Series B, 47, 203–210.

Beal, S. L. and Sheiner, L. B. (1982), “Estimating Population Kinetics,” CRC Critical Reviews in Biomedical Engineering, 8, 195–222.

Beal, S. L. and Sheiner, L. B. (1988), “Heteroscedastic Nonlinear Regression,” Technometrics, 30, 327–338.

Beal, S. L. and Sheiner, L. B. (1992), NONMEM User’s Guide, San Francisco: NONMEM Project Group, University of California, San Francisco.

Beale, E. M. L. (1972), “A Derivation of Conjugate Gradients,” in F. A. Lootsma, ed., Numerical Methods for Nonlinear Optimization, London: Academic Press.

Beitler, P. J. and Landis, J. R. (1985), “A Mixed-Effects Model for Categorical Data,” Biometrics, 41, 991–1000.

Billingsley, P. (1986), Probability and Measure, Second Edition, New York: John Wiley & Sons.

Booth, J. G. and Hobert, J. P. (1998), “Standard Errors of Prediction in Generalized Linear Mixed Models,” Journal of the American Statistical Association, 93, 262–272.

Breslow, N. E. and Clayton, D. G. (1993), “Approximate Inference in Generalized Linear Mixed Models,” Journal of the American Statistical Association, 88, 9–25.

Burnham, K. P. and Anderson, D. R. (1998), Model Selection and Inference: A Practical Information-Theoretic Approach, New York: Springer-Verlag.

Cox, C. (1998), “Delta Method,” Encyclopedia of Biostatistics, 1125–1127.

Cox, D. R. and Oakes, D. (1984), Analysis of Survival Data, London: Chapman & Hall.

Cramer, J. S. (1986), Econometric Applications of Maximum Likelihood Methods, Cambridge: Cambridge University Press.

Crouch, E. A. C. and Spiegelman, D. (1990), “The Evaluation of Integrals of the Form 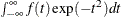: Application to Logistic-Normal Models,” Journal of the American Statistical Association, 85, 464–469.

Davidian, M. and Gallant, R. A. (1993), “The Nonlinear Mixed Effects Model with a Smooth Random Effects Density,” Biometrika, 80, 475–488.

Davidian, M. and Giltinan, D. M. (1995), Nonlinear Models for Repeated Measurement Data, New York: Chapman & Hall.

Dennis, J. E., Gay, D. M., and Welsch, R. E. (1981), “An Adaptive Nonlinear Least-Squares Algorithm,” ACM Transactions on Mathematical Software, 7, 348–368.

Dennis, J. E. and Mei, H. H. W. (1979), “Two New Unconstrained Optimization Algorithms Which Use Function and Gradient Values,” Journal of Optimization Theory Applications, 28, 453–482.

Dennis, J. E. and Schnabel, R. B. (1983), Numerical Methods for Unconstrained Optimization and Nonlinear Equations, Englewood, NJ: Prentice-Hall.

Diggle, P. J., Liang, K.-Y., and Zeger, S. L. (1994), Analysis of Longitudinal Data, Oxford: Clarendon Press.

Draper, D. (1996), “Discussion of the Paper by Lee and Nelder,” Journal of the Royal Statistical Society, Series B, 58, 662–663.

Draper, N. R. and Smith, H. (1981), Applied Regression Analysis, Second Edition, New York: John Wiley & Sons.

Engel, B. and Keen, A. (1992), A Simple Approach for the Analysis of Generalized Linear Mixed Models, volume LWA-92-6, Wageningen, Netherlands: Agricultural Mathematics Group (GLW-DLO).

Eskow, E. and Schnabel, R. B. (1991), “Algorithm 695: Software for a New Modified Cholesky Factorization,” ACM Transactions on Mathematical Software, 17, 306–312.

Ezzet, F. and Whitehead, J. (1991), “A Random Effects Model for Ordinal Responses from a Crossover Trial,” Statistics in Medicine, 10, 901–907.

Fletcher, R. (1987), Practical Methods of Optimization, Second Edition, Chichester, UK: John Wiley & Sons.

Galecki, A. T. (1998), “NLMEM: New SAS/IML Macro for Hierarchical Nonlinear Models,” Computer Methods and Programs in Biomedicine, 55, 207–216.

Gallant, A. R. (1987), Nonlinear Statistical Models, New York: John Wiley & Sons.

Gaver, D. P. and O’Muircheartaigh, I. G. (1987), “Robust Empirical Bayes Analysis of Event Rates,” Technometrics, 29, 1–15.

Gay, D. M. (1983), “Subroutines for Unconstrained Minimization,” ACM Transactions on Mathematical Software, 9, 503–524.

Gilmour, A. R., Anderson, R. D., and Rae, A. L. (1985), “The Analysis of Binomial Data by Generalized Linear Mixed Model,” Biometrika, 72, 593–599.

Goldstein, H. (1991), “Nonlinear Multilevel Models, with an Application to Discrete Response Data,” Biometrika, 78, 45–51.

Golub, G. H. and Welsch, J. H. (1969), “Calculation of Gaussian Quadrature Rules,” Mathematical Computing, 23, 221–230.

Harville, D. A. and Mee, R. W. (1984), “A Mixed-Model Procedure for Analyzing Ordered Categorical Data,” Biometrics, 40, 393–408.

Hedeker, D. and Gibbons, R. D. (1994), “A Random Effects Ordinal Regression Model for Multilevel Analysis,” Biometrics, 50, 933–944.

Hurvich, C. M. and Tsai, C.-L. (1989), “Regression and Time Series Model Selection in Small Samples,” Biometrika, 76, 297–307.

Lin, X. and Breslow, N. E. (1996), “Bias Correction in Generalized Linear Mixed Models with Multiple Components of Dispersion,” Journal of the American Statistical Association, 91, 1007–1016.

Lindstrom, M. J. and Bates, D. M. (1990), “Nonlinear Mixed Effects Models for Repeated Measures Data,” Biometrics, 46, 673–687.

Littell, R. C., Milliken, G. A., Stroup, W. W., Wolfinger, R. D., and Schabenberger, O. (2006), SAS for Mixed Models, Second Edition, Cary, NC: SAS Press.

Liu, Q. and Pierce, D. A. (1994), “A Note on Gauss-Hermite Quadrature,” Biometrika, 81, 624–629.

Longford, N. T. (1994), “Logistic Regression with Random Coefficients,” Computational Statistics and Data Analysis, 17, 1–15.

McCulloch, C. E. (1994), “Maximum Likelihood Variance Components Estimation for Binary Data,” Journal of the American Statistical Association, 89, 330–335.

McGilchrist, C. E. (1994), “Estimation in Generalized Mixed Models,” Journal of the Royal Statistical Society, Series B, 56, 61–69.

Moré, J. J. (1978), “The Levenberg-Marquardt Algorithm: Implementation and Theory,” in G. A. Watson, ed., Lecture Notes in Mathematics, volume 30, 105–116, Berlin: Springer-Verlag.

Moré, J. J. and Sorensen, D. C. (1983), “Computing a Trust-Region Step,” SIAM Journal on Scientific and Statistical Computing, 4, 553–572.

Ochi, Y. and Prentice, R. L. (1984), “Likelihood Inference in a Correlated Probit Regression Model,” Biometrika, 71, 531–543.

Pierce, D. A. and Sands, B. R. (1975), Extra-Bernoulli Variation in Binary Data, Technical Report 46, Department of Statistics, Oregon State University.

Pinheiro, J. C. and Bates, D. M. (1995), “Approximations to the Log-Likelihood Function in the Nonlinear Mixed-Effects Model,” Journal of Computational and Graphical Statistics, 4, 12–35.

Polak, E. (1971), Computational Methods in Optimization, New York: Academic Press.

Powell, M. J. D. (1977), “Restart Procedures for the Conjugate Gradient Method,” Mathematical Programming, 12, 241–254.

Pringle, R. M. and Rayner, A. A. (1971), Generalized Inverse Matrices with Applications to Statistics, New York: Hafner Publishing.

Rodriguez, G. and Goldman, N. (1995), “An Assessment of Estimation Procedures for Multilevel Models with Binary Response,” Journal of the Royal Statistical Society, Series A, 158, 73–89.

Roe, D. J. (1997), “Comparison of Population Pharmacokinetic Modeling Methods Using Simulated Data: Results from the Population Modeling Workgroup,” Statistics in Medicine, 16, 1241–1262.

Schall, R. (1991), “Estimation in Generalized Linear Models with Random Effects,” Biometrika, 78, 719–727.

Schittkowski, K. and Stoer, J. (1979), “A Factorization Method for the Solution of Constrained Linear Least Squares Problems Allowing Subsequent Data Changes,” Numerische Mathematik, 31, 431–463.

Self, S. G. and Liang, K.-Y. (1987), “Asymptotic Properties of Maximum Likelihood Estimators and Likelihood Ratio Tests under Nonstandard Conditions,” Journal of the American Statistical Association, 82, 605–610.

Serfling, R. J. (1980), Approximation Theorems of Mathematical Statistics, New York: John Wiley & Sons.

Sheiner, L. B. and Beal, S. L. (1980), “Evaluation of Methods for Estimating Population Pharmacokinetic Parameters. I. Michaelis-Menten Model: Routine Clinical Pharmacokinetic Data,” Journal of Pharmacokinetics and Biopharmaceutics, 8, 553–571.

Sheiner, L. B. and Beal, S. L. (1985), “Pharmacokinetic Parameter Estimates from Several Least Squares Procedures: Superiority of Extended Least Squares,” Journal of Pharmacokinetics and Biopharmaceutics, 13, 185–201.

Smith, S. P. (1995), “Differentiation of the Cholesky Algorithm,” Journal of Computational and Graphical Statistics, 4, 134–147.

Stiratelli, R., Laird, N. M., and Ware, J. H. (1984), “Random Effects Models for Serial Observations with Binary Response,” Biometrics, 40, 961–971.

Vonesh, E. F. (1992), “Nonlinear Models for the Analysis of Longitudinal Data,” Statistics in Medicine, 11, 1929–1954.

Vonesh, E. F. (1996), “A Note on Laplace’s Approximation for Nonlinear Mixed-Effects Models,” Biometrika, 83, 447–452.

Vonesh, E. F. and Chinchilli, V. M. (1997), Linear and Nonlinear Models for the Analysis of Repeated Measurements, New York: Marcel Dekker.

Weil, C. S. (1970), “Selection of the Valid Number of Sampling Units and Consideration of Their Combination in Toxicological Studies Involving Reproduction, Teratogenesis, or Carcinogenesis,” Food and Cosmetic Toxicology, 8, 177–182.

White, H. (1982), “Maximum Likelihood Estimation of Misspecified Models,” Econometrica, 50, 1–25.

Williams, D. A. (1975), “The Analysis of Binary Responses from Toxicological Experiments Involving Reproduction and Teratogenicity,” Biometrics, 31, 949–952.

Wolfinger, R. D. (1993), “Laplace’s Approximation for Nonlinear Mixed Models,” Biometrika, 80, 791–795.

Wolfinger, R. D. (1997), “Comment: Experiences with the SAS Macro NLINMIX,” Statistics in Medicine, 16, 1258–1259.

Wolfinger, R. D. and Lin, X. (1997), “Two Taylor-Series Approximation Methods for Nonlinear Mixed Models,” Computational Statistics and Data Analysis, 25, 465–490.

Wolfinger, R. D. and O’Connell, M. (1993), “Generalized Linear Mixed Models: A Pseudo-likelihood Approach,” Journal of Statistical Computation and Simulation, 48, 233–243.

Yuh, L., Beal, S., Davidian, M., Harrison, F., Hester, A., Kowalski, K., Vonesh, E., and Wolfinger, R. D. (1994), “Population Pharmacokinetic/Pharmacodynamic Methodology and Applications: A Bibliography,” Biometrics, 50, 566–575.