The NLMIXED Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 Modeling Assumptions and NotationIntegral ApproximationsBuilt-in Log-Likelihood FunctionsOptimization AlgorithmsFinite-Difference Approximations of DerivativesHessian ScalingActive Set MethodsLine-Search MethodsRestricting the Step LengthComputational ProblemsCovariance MatrixPredictionComputational ResourcesDisplayed OutputODS Table Names
Modeling Assumptions and NotationIntegral ApproximationsBuilt-in Log-Likelihood FunctionsOptimization AlgorithmsFinite-Difference Approximations of DerivativesHessian ScalingActive Set MethodsLine-Search MethodsRestricting the Step LengthComputational ProblemsCovariance MatrixPredictionComputational ResourcesDisplayed OutputODS Table Names -
Examples

- References
Example 64.5 Failure Time and Frailty Model
In this example an accelerated failure time model with proportional hazard is fitted with and without random effects. The
data are from the “Getting Started” example of PROC LIFEREG; see Chapter 51: The LIFEREG Procedure. Thirty-eight patients are divided into two groups of equal size, and different pain relievers are assigned to each group.
The outcome reported is the time in minutes until headache relief. The variable censor indicates whether relief was observed during the course of the observation period (censor = 0) or whether the observation is censored (censor = 1). The SAS DATA step for these data is as follows:
data headache; input minutes group censor @@; patient = _n_; datalines; 11 1 0 12 1 0 19 1 0 19 1 0 19 1 0 19 1 0 21 1 0 20 1 0 21 1 0 21 1 0 20 1 0 21 1 0 20 1 0 21 1 0 25 1 0 27 1 0 30 1 0 21 1 1 24 1 1 14 2 0 16 2 0 16 2 0 21 2 0 21 2 0 23 2 0 23 2 0 23 2 0 23 2 0 25 2 1 23 2 0 24 2 0 24 2 0 26 2 1 32 2 1 30 2 1 30 2 0 32 2 1 20 2 1 ;
In modeling survival data, censoring of observations must be taken into account carefully. In this example, only right censoring
occurs. If ![]() ,
, ![]() , and
, and ![]() denote the density of failure, the hazard function, and the survival distribution function at time t, respectively, then the log likelihood can be written as
denote the density of failure, the hazard function, and the survival distribution function at time t, respectively, then the log likelihood can be written as
|
|
|
|
|
|
(See Cox and Oakes 1984, Ch. 3.) In these expressions ![]() is the set of uncensored observations,
is the set of uncensored observations, ![]() is the set of censored observations, and n denotes the total sample size.
is the set of censored observations, and n denotes the total sample size.
The proportional hazards specification expresses the hazard in terms of a baseline hazard, multiplied by a constant. In this
example the hazard is that of a Weibull model and is parameterized as ![]() and
and ![]() .
.
The linear predictor is set equal to the intercept in the reference group (group = 2); this defines the baseline hazard. The corresponding distribution of survival past time t is ![]() . See Cox and Oakes (1984, Table 2.1) and the section “Supported Distributions” in Chapter 51: The LIFEREG Procedure, for this and other survival distribution models and various parameterizations.
. See Cox and Oakes (1984, Table 2.1) and the section “Supported Distributions” in Chapter 51: The LIFEREG Procedure, for this and other survival distribution models and various parameterizations.
The following NLMIXED statements fit this accelerated failure time model and estimate the cumulative distribution function of time to headache relief:
proc nlmixed data=headache; bounds gamma > 0; linp = b0 - b1*(group-2); alpha = exp(-linp); G_t = exp(-(alpha*minutes)**gamma); g = gamma*alpha*((alpha*minutes)**(gamma-1))*G_t; ll = (censor=0)*log(g) + (censor=1)*log(G_t); model minutes ~ general(ll); predict 1-G_t out=cdf; run;
Output 64.5.1: Specifications Table for Fixed-Effects Failure Time Model
| Specifications | |
|---|---|
| Data Set | WORK.HEADACHE |
| Dependent Variable | minutes |
| Distribution for Dependent Variable | General |
| Optimization Technique | Dual Quasi-Newton |
| Integration Method | None |
The “Specifications” table shows that no integration is required, since the model does not contain random effects (Output 64.5.1).
Output 64.5.2: Negative Log Likelihood with Default Starting Values
| Parameters | |||
|---|---|---|---|
| gamma | b0 | b1 | NegLogLike |
| 1 | 1 | 1 | 263.990327 |
No starting values were given for the three parameters. The NLMIXED procedure assigns the default value of 1.0 in this case. The negative log likelihood based on these starting values is shown in Output 64.5.2.
Output 64.5.3: Iteration History for Fixed-Effects Failure Time Model
| Iteration History | ||||||
|---|---|---|---|---|---|---|
| Iter | Calls | NegLogLike | Diff | MaxGrad | Slope | |
| 1 | 2 | 169.244311 | 94.74602 | 22.5599 | -2230.83 | |
| 2 | 4 | 142.873508 | 26.3708 | 14.88631 | -3.64643 | |
| 3 | 6 | 140.633695 | 2.239814 | 11.25234 | -9.49454 | |
| 4 | 8 | 122.890659 | 17.74304 | 19.44959 | -2.50807 | |
| 5 | 9 | 121.396959 | 1.493699 | 13.85584 | -4.55427 | |
| 6 | 11 | 120.623843 | 0.773116 | 13.67062 | -1.38064 | |
| 7 | 12 | 119.278196 | 1.345647 | 15.78014 | -1.69072 | |
| 8 | 14 | 116.271325 | 3.006871 | 26.94029 | -3.2529 | |
| 9 | 16 | 109.427401 | 6.843925 | 19.88382 | -6.9289 | |
| 10 | 19 | 103.298102 | 6.129298 | 12.15647 | -4.96054 | |
| 11 | 22 | 101.686239 | 1.611863 | 14.24868 | -4.34059 | |
| 12 | 23 | 100.027875 | 1.658364 | 11.69853 | -13.2049 | |
| 13 | 26 | 99.9189048 | 0.108971 | 3.602552 | -0.55176 | |
| 14 | 28 | 99.8738836 | 0.045021 | 0.170712 | -0.16645 | |
| 15 | 30 | 99.8736392 | 0.000244 | 0.050822 | -0.00041 | |
| 16 | 32 | 99.8736351 | 4.071E-6 | 0.000705 | -6.9E-6 | |
| 17 | 34 | 99.8736351 | 6.1E-10 | 4.768E-6 | -1.23E-9 | |
| NOTE: GCONV convergence criterion satisfied. |
The “Iteration History” table shows that the procedure converges after 17 iterations and 34 evaluations of the objective function (Output 64.5.3).
Output 64.5.4: Fit Statistics and Parameter Estimates
| Fit Statistics | |
|---|---|
| -2 Log Likelihood | 199.7 |
| AIC (smaller is better) | 205.7 |
| AICC (smaller is better) | 206.5 |
| BIC (smaller is better) | 210.7 |
| Parameter Estimates | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | Estimate | Standard Error | DF | t Value | Pr > |t| | Alpha | Lower | Upper | Gradient |
| gamma | 4.7128 | 0.6742 | 38 | 6.99 | <.0001 | 0.05 | 3.3479 | 6.0777 | 5.327E-8 |
| b0 | 3.3091 | 0.05885 | 38 | 56.23 | <.0001 | 0.05 | 3.1900 | 3.4283 | -4.77E-6 |
| b1 | -0.1933 | 0.07856 | 38 | -2.46 | 0.0185 | 0.05 | -0.3523 | -0.03426 | -1.22E-6 |
The parameter estimates and their standard errors shown in Output 64.5.4 are identical to those obtained with the LIFEREG procedure and the following statements:
proc lifereg data=headache; class group; model minutes*censor(1) = group / dist=weibull; output out=new cdf=prob; run;
The t statistic and confidence limits are based on 38 degrees of freedom. The LIFEREG procedure computes z intervals for the parameter estimates.
For the two groups you obtain
|
|
|
|
|
|
The probabilities of headache relief by t minutes are estimated as
|
|
|
|
|
|
These probabilities, calculated at the observed times, are shown for the two groups in Output 64.5.5 and printed with the following statements:
proc print data=cdf; var group censor patient minutes pred; run;
Since the slope estimate is negative with p-value of 0.0185, you can infer that pain reliever 1 leads to overall significantly faster relief, but the estimated probabilities give no information about patient-to-patient variation within and between groups. For example, while pain reliever 1 provides faster relief overall, some patients in group 2 might respond more quickly than some patients in group 1. A frailty model enables you to accommodate and estimate patient-to-patient variation in health status by introducing random effects into a subject’s hazard function.
Output 64.5.5: Estimated Cumulative Distribution Function
| Obs | group | censor | patient | minutes | Pred |
|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 11 | 0.03336 |
| 2 | 1 | 0 | 2 | 12 | 0.04985 |
| 3 | 1 | 0 | 3 | 19 | 0.35975 |
| 4 | 1 | 0 | 4 | 19 | 0.35975 |
| 5 | 1 | 0 | 5 | 19 | 0.35975 |
| 6 | 1 | 0 | 6 | 19 | 0.35975 |
| 7 | 1 | 0 | 7 | 21 | 0.51063 |
| 8 | 1 | 0 | 8 | 20 | 0.43325 |
| 9 | 1 | 0 | 9 | 21 | 0.51063 |
| 10 | 1 | 0 | 10 | 21 | 0.51063 |
| 11 | 1 | 0 | 11 | 20 | 0.43325 |
| 12 | 1 | 0 | 12 | 21 | 0.51063 |
| 13 | 1 | 0 | 13 | 20 | 0.43325 |
| 14 | 1 | 0 | 14 | 21 | 0.51063 |
| 15 | 1 | 0 | 15 | 25 | 0.80315 |
| 16 | 1 | 0 | 16 | 27 | 0.90328 |
| 17 | 1 | 0 | 17 | 30 | 0.97846 |
| 18 | 1 | 1 | 18 | 21 | 0.51063 |
| 19 | 1 | 1 | 19 | 24 | 0.73838 |
| 20 | 2 | 0 | 20 | 14 | 0.04163 |
| 21 | 2 | 0 | 21 | 16 | 0.07667 |
| 22 | 2 | 0 | 22 | 16 | 0.07667 |
| 23 | 2 | 0 | 23 | 21 | 0.24976 |
| 24 | 2 | 0 | 24 | 21 | 0.24976 |
| 25 | 2 | 0 | 25 | 23 | 0.35674 |
| 26 | 2 | 0 | 26 | 23 | 0.35674 |
| 27 | 2 | 0 | 27 | 23 | 0.35674 |
| 28 | 2 | 0 | 28 | 23 | 0.35674 |
| 29 | 2 | 1 | 29 | 25 | 0.47982 |
| 30 | 2 | 0 | 30 | 23 | 0.35674 |
| 31 | 2 | 0 | 31 | 24 | 0.41678 |
| 32 | 2 | 0 | 32 | 24 | 0.41678 |
| 33 | 2 | 1 | 33 | 26 | 0.54446 |
| 34 | 2 | 1 | 34 | 32 | 0.87656 |
| 35 | 2 | 1 | 35 | 30 | 0.78633 |
| 36 | 2 | 0 | 36 | 30 | 0.78633 |
| 37 | 2 | 1 | 37 | 32 | 0.87656 |
| 38 | 2 | 1 | 38 | 20 | 0.20414 |
The following statements model the hazard for patient i in terms of ![]() , where
, where ![]() is a (normal) random patient effect. Notice that the only difference from the previous NLMIXED statements are the RANDOM statement and the addition of
is a (normal) random patient effect. Notice that the only difference from the previous NLMIXED statements are the RANDOM statement and the addition of z in the linear predictor. The empirical Bayes estimates of the random effect (RANDOM statement), the parameter estimates (ODS OUTPUT statement), and the estimated cumulative distribution function (PREDICT statement) are saved to subsequently graph the patient-specific distribution functions.
ods output ParameterEstimates=est; proc nlmixed data=headache; bounds gamma > 0; linp = b0 - b1*(group-2) + z; alpha = exp(-linp); G_t = exp(-(alpha*minutes)**gamma); g = gamma*alpha*((alpha*minutes)**(gamma-1))*G_t; ll = (censor=0)*log(g) + (censor=1)*log(G_t); model minutes ~ general(ll); random z ~ normal(0,exp(2*logsig)) subject=patient out=EB; predict 1-G_t out=cdf; run;
Output 64.5.6: Specifications for Random Frailty Model
| Specifications | |
|---|---|
| Data Set | WORK.HEADACHE |
| Dependent Variable | minutes |
| Distribution for Dependent Variable | General |
| Random Effects | z |
| Distribution for Random Effects | Normal |
| Subject Variable | patient |
| Optimization Technique | Dual Quasi-Newton |
| Integration Method | Adaptive Gaussian Quadrature |
The “Specifications” table shows that the objective function is computed by adaptive Gaussian quadrature because of the presence of random effects (compare Output 64.5.6 and Output 64.5.1). The “Dimensions” table reports that nine quadrature points are being used to integrate over the random effects (Output 64.5.7).
Output 64.5.7: Dimensions Table for Random Frailty Model
| Dimensions | |
|---|---|
| Observations Used | 38 |
| Observations Not Used | 0 |
| Total Observations | 38 |
| Subjects | 38 |
| Max Obs Per Subject | 1 |
| Parameters | 4 |
| Quadrature Points | 9 |
Output 64.5.8: Iteration History for Random Frailty Model
| Iteration History | ||||||
|---|---|---|---|---|---|---|
| Iter | Calls | NegLogLike | Diff | MaxGrad | Slope | |
| 1 | 5 | 142.121411 | 28.82225 | 12.14484 | -88.8664 | |
| 2 | 7 | 136.440369 | 5.681042 | 25.93096 | -65.7217 | |
| 3 | 9 | 122.972041 | 13.46833 | 46.56546 | -146.887 | |
| 4 | 11 | 120.904825 | 2.067216 | 23.77936 | -94.2862 | |
| 5 | 13 | 109.224144 | 11.68068 | 57.65493 | -92.4075 | |
| 6 | 15 | 105.064733 | 4.159411 | 4.824649 | -19.5879 | |
| 7 | 16 | 101.902207 | 3.162526 | 14.1287 | -6.33767 | |
| 8 | 18 | 99.6907395 | 2.211468 | 7.676822 | -3.42364 | |
| 9 | 20 | 99.3654033 | 0.325336 | 5.689204 | -0.93978 | |
| 10 | 22 | 99.2602178 | 0.105185 | 0.317643 | -0.23408 | |
| 11 | 24 | 99.254434 | 0.005784 | 1.17351 | -0.00556 | |
| 12 | 25 | 99.2456973 | 0.008737 | 0.247412 | -0.00871 | |
| 13 | 27 | 99.2445445 | 0.001153 | 0.104942 | -0.00218 | |
| 14 | 29 | 99.2444958 | 0.000049 | 0.005646 | -0.0001 | |
| 15 | 31 | 99.2444957 | 9.147E-8 | 0.000271 | -1.84E-7 | |
| NOTE: GCONV convergence criterion satisfied. |
The procedure converges after 15 iterations (Output 64.5.8). The achieved –2 log likelihood is only 1.2 less than that in the model without random effects (compare Output 64.5.9 and Output 64.5.4). Compared to a chi-square distribution with one degree of freedom, the addition of the random effect appears not to improve the model significantly. You must exercise care, however, in interpreting likelihood ratio tests when the value under the null hypothesis falls on the boundary of the parameter space (see, for example, Self and Liang 1987).
Output 64.5.9: Fit Statistics for Random Frailty Model
| Fit Statistics | |
|---|---|
| -2 Log Likelihood | 198.5 |
| AIC (smaller is better) | 206.5 |
| AICC (smaller is better) | 207.7 |
| BIC (smaller is better) | 213.0 |
Output 64.5.10: Parameter Estimates
| Parameter Estimates | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | Estimate | Standard Error | DF | t Value | Pr > |t| | Alpha | Lower | Upper | Gradient |
| gamma | 6.2867 | 2.1334 | 37 | 2.95 | 0.0055 | 0.05 | 1.9641 | 10.6093 | -1.89E-7 |
| b0 | 3.2786 | 0.06576 | 37 | 49.86 | <.0001 | 0.05 | 3.1453 | 3.4118 | 0.000271 |
| b1 | -0.1761 | 0.08264 | 37 | -2.13 | 0.0398 | 0.05 | -0.3436 | -0.00868 | 0.000111 |
| logsig | -1.9027 | 0.5273 | 37 | -3.61 | 0.0009 | 0.05 | -2.9711 | -0.8343 | 0.000027 |
The estimate of the Weibull parameter has changed drastically from the model without random effects (compare Output 64.5.10 and Output 64.5.4). The variance of the patient random effect is ![]() . The listing in Output 64.5.11 shows the empirical Bayes estimates of the random effects. These are the adjustments made to the linear predictor in order
to obtain a patient’s survival distribution. The listing is produced with the following statements:
. The listing in Output 64.5.11 shows the empirical Bayes estimates of the random effects. These are the adjustments made to the linear predictor in order
to obtain a patient’s survival distribution. The listing is produced with the following statements:
proc print data=eb; var Patient Effect Estimate StdErrPred; run;
Output 64.5.11: Empirical Bayes Estimates of Random Effects
| Obs | patient | Effect | Estimate | StdErrPred |
|---|---|---|---|---|
| 1 | 1 | z | -0.13597 | 0.23249 |
| 2 | 2 | z | -0.13323 | 0.22793 |
| 3 | 3 | z | -0.06294 | 0.13813 |
| 4 | 4 | z | -0.06294 | 0.13813 |
| 5 | 5 | z | -0.06294 | 0.13813 |
| 6 | 6 | z | -0.06294 | 0.13813 |
| 7 | 7 | z | -0.02568 | 0.11759 |
| 8 | 8 | z | -0.04499 | 0.12618 |
| 9 | 9 | z | -0.02568 | 0.11759 |
| 10 | 10 | z | -0.02568 | 0.11759 |
| 11 | 11 | z | -0.04499 | 0.12618 |
| 12 | 12 | z | -0.02568 | 0.11759 |
| 13 | 13 | z | -0.04499 | 0.12618 |
| 14 | 14 | z | -0.02568 | 0.11759 |
| 15 | 15 | z | 0.05980 | 0.11618 |
| 16 | 16 | z | 0.10458 | 0.12684 |
| 17 | 17 | z | 0.17147 | 0.14550 |
| 18 | 18 | z | 0.06471 | 0.13807 |
| 19 | 19 | z | 0.11157 | 0.14604 |
| 20 | 20 | z | -0.13406 | 0.22899 |
| 21 | 21 | z | -0.12698 | 0.21667 |
| 22 | 22 | z | -0.12698 | 0.21667 |
| 23 | 23 | z | -0.08506 | 0.15701 |
| 24 | 24 | z | -0.08506 | 0.15701 |
| 25 | 25 | z | -0.05797 | 0.13294 |
| 26 | 26 | z | -0.05797 | 0.13294 |
| 27 | 27 | z | -0.05797 | 0.13294 |
| 28 | 28 | z | -0.05797 | 0.13294 |
| 29 | 29 | z | 0.06420 | 0.13956 |
| 30 | 30 | z | -0.05797 | 0.13294 |
| 31 | 31 | z | -0.04266 | 0.12390 |
| 32 | 32 | z | -0.04266 | 0.12390 |
| 33 | 33 | z | 0.07618 | 0.14132 |
| 34 | 34 | z | 0.16292 | 0.16460 |
| 35 | 35 | z | 0.13193 | 0.15528 |
| 36 | 36 | z | 0.06327 | 0.12124 |
| 37 | 37 | z | 0.16292 | 0.16460 |
| 38 | 38 | z | 0.02074 | 0.14160 |
The predicted values and patient-specific survival distributions can be plotted with the SAS code that follows:
proc transpose data=est(keep=estimate)
out=trest(rename=(col1=gamma col2=b0 col3=b1));
run;
data pred;
merge eb(keep=estimate) headache(keep=patient group);
array pp{2} pred1-pred2;
if _n_ = 1 then set trest(keep=gamma b0 b1);
do time=11 to 32;
linp = b0 - b1*(group-2) + estimate;
pp{group} = 1-exp(- (exp(-linp)*time)**gamma);
symbolid = patient+1;
output;
end;
keep pred1 pred2 time patient;
run;
data pred;
merge pred
cdf(where = (group=1)
rename = (pred=pcdf1 minutes=minutes1)
keep = pred minutes group)
cdf(where = (group=2)
rename = (pred=pcdf2 minutes=minutes2)
keep = pred minutes group);
drop group;
run;
proc sgplot data=pred noautolegend;
label minutes1='Minutes to Headache Relief'
pcdf1 ='Estimated Patient-specific CDF';
series x=time y=pred1 /
group=patient
lineattrs=(pattern=solid color=black);
series x=time y=pred2 /
group=patient
lineattrs=(pattern=dash color=black);
scatter x=minutes1 y=pcdf1 /
markerattrs=(symbol=CircleFilled size=9);
scatter x=minutes2 y=pcdf2 /
markerattrs=(symbol=Circle size=9);
run;
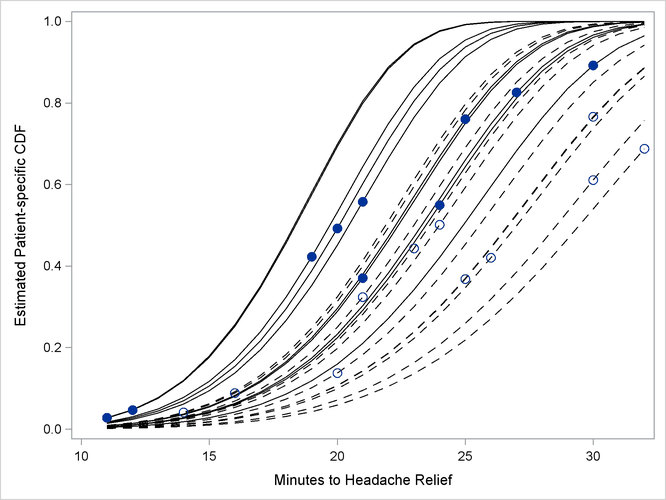
The separation of the distribution functions by groups is evident in Output 64.5.12. Most of the distributions of patients in the first group are to the left of the distributions in the second group. The separation is not complete, however. Several patients who are assigned the second pain reliever experience headache relief more quickly than patients assigned to the first group.
Output 64.5.12: Patient-Specific CDFs and Predicted Values. Pain Reliever 1: Solid Lines, Closed Circles; Pain Reliever 2: Dashed Lines, Open Circles.