The REG Procedure

Simple Linear Regression

Suppose that a response variable Y can be predicted by a linear function of a regressor variable X. You can estimate $\beta _0$ , the intercept, and $\beta _1$ , the slope, in

$Y_ i = \beta _0 + \beta _1 X_ i + \epsilon _ i$

for the observations $i=1,2,\ldots ,n$ . Fitting this model with the REG procedure requires only the following MODEL statement, where y is the outcome variable and x is the regressor variable.

proc reg;
   model y=x;
run;

For example, you might use regression analysis to find out how well you can predict a child’s weight if you know that child’s height. The Class data set used in this example is available in the Sashelp library.

The equation of interest is

$\mbox{\Variable{Weight}} = \beta _0 + \beta _1 \mbox{\Variable{Height}} + \epsilon$

The variable Weight is the response or dependent variable in this equation, and $\beta _0$ and $\beta _1$ are the unknown parameters to be estimated. The variable Height is the regressor or independent variable, and $\epsilon$ is the unknown error. The following commands invoke the REG procedure and fit this model to the data.

ods graphics on;

proc reg data=sashelp.class;
   model Weight = Height;
run;

ods graphics off;

Figure 79.1 includes some information concerning model fit.

The F statistic for the overall model is highly significant (F = 57.076, p < 0.0001), indicating that the model explains a significant portion of the variation in the data.

The degrees of freedom can be used in checking accuracy of the data and model. The model degrees of freedom are one less than the number of parameters to be estimated. This model estimates two parameters, $\beta _0$ and $\beta _1$ ; thus, the degrees of freedom should be 2 – 1 = 1. The corrected total degrees of freedom are always one less than the total number of observations in the data set, in this case 19 – 1 = 18.

Several simple statistics follow the ANOVA table. The Root MSE is an estimate of the standard deviation of the error term. The coefficient of variation, or Coeff Var, is a unitless expression of the variation in the data. The R-square and Adj R-square are two statistics used in assessing the fit of the model; values close to 1 indicate a better fit. The R-square of 0.77 indicates that Height accounts for 77% of the variation in Weight.

Figure 79.1: ANOVA Table

The REG Procedure

Model: MODEL1

Dependent Variable: Weight

Analysis of Variance
Source	DF	Sum of Squares	Mean Square	F Value	Pr > F
Model	1	7193.24912	7193.24912	57.08	<.0001
Error	17	2142.48772	126.02869
Corrected Total	18	9335.73684

Root MSE	11.22625	R-Square	0.7705
Dependent Mean	100.02632	Adj R-Sq	0.7570
Coeff Var	11.22330

The “Parameter Estimates” table in Figure 79.2 contains the estimates of $\beta _0$ and $\beta _1$ . The table also contains the t statistics and the corresponding p-values for testing whether each parameter is significantly different from zero. The p-values (t = –4.43, p = 0.0004 and t = 7.55, p < 0.0001) indicate that the intercept and Height parameter estimates, respectively, are highly significant.

From the parameter estimates, the fitted model is

$\mbox{\Variable{Weight}} = -143.0 + 3.9 \times \mbox{\Variable{Height}}$

Figure 79.2: Parameter Estimates

Parameter Estimates
Variable	DF	Parameter Estimate	Standard Error	t Value	Pr > \|t\|
Intercept	1	-143.02692	32.27459	-4.43	0.0004
Height	1	3.89903	0.51609	7.55	<.0001

If ODS Graphics is enabled, then PROC REG produces a variety of plots. Figure 79.3 shows a plot of the residuals versus the regressor and Figure 79.4 shows a panel of diagnostic plots.

Figure 79.3: Residuals vs. Regressor

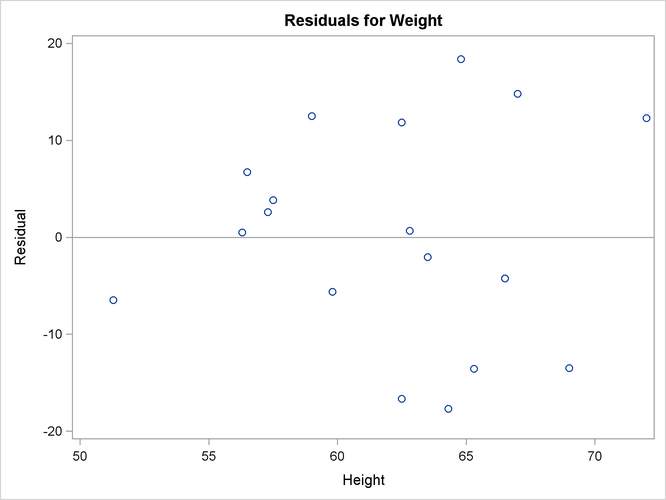
Figure 79.4: Fit Diagnostics

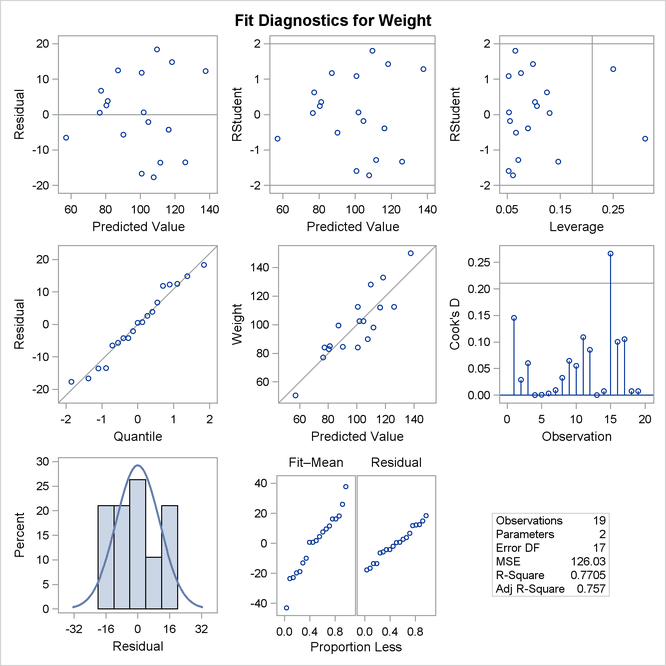
A trend in the residuals would indicate nonconstant variance in the data. The plot of residuals by predicted values in the upper-left corner of the diagnostics panel in Figure 79.4 might indicate a slight trend in the residuals; they appear to increase slightly as the predicted values increase. A fan-shaped trend might indicate the need for a variance-stabilizing transformation. A curved trend (such as a semicircle) might indicate the need for a quadratic term in the model. Since these residuals have no apparent trend, the analysis is considered to be acceptable.