The GLM Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 Statistical Assumptions for Using PROC GLMSpecification of EffectsUsing PROC GLM InteractivelyParameterization of PROC GLM ModelsHypothesis Testing in PROC GLMEffect Size Measures for F Tests in GLMAbsorptionSpecification of ESTIMATE ExpressionsComparing GroupsMultivariate Analysis of VarianceRepeated Measures Analysis of VarianceRandom-Effects AnalysisMissing ValuesComputational ResourcesComputational MethodOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
Statistical Assumptions for Using PROC GLMSpecification of EffectsUsing PROC GLM InteractivelyParameterization of PROC GLM ModelsHypothesis Testing in PROC GLMEffect Size Measures for F Tests in GLMAbsorptionSpecification of ESTIMATE ExpressionsComparing GroupsMultivariate Analysis of VarianceRepeated Measures Analysis of VarianceRandom-Effects AnalysisMissing ValuesComputational ResourcesComputational MethodOutput Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples
 Randomized Complete Blocks with Means Comparisons and ContrastsRegression with Mileage DataUnbalanced ANOVA for Two-Way Design with InteractionAnalysis of CovarianceThree-Way Analysis of Variance with ContrastsMultivariate Analysis of VarianceRepeated Measures Analysis of VarianceMixed Model Analysis of Variance with the RANDOM StatementAnalyzing a Doubly Multivariate Repeated Measures DesignTesting for Equal Group VariancesAnalysis of a Screening Design
Randomized Complete Blocks with Means Comparisons and ContrastsRegression with Mileage DataUnbalanced ANOVA for Two-Way Design with InteractionAnalysis of CovarianceThree-Way Analysis of Variance with ContrastsMultivariate Analysis of VarianceRepeated Measures Analysis of VarianceMixed Model Analysis of Variance with the RANDOM StatementAnalyzing a Doubly Multivariate Repeated Measures DesignTesting for Equal Group VariancesAnalysis of a Screening Design - References
In polynomial regression, the values of a dependent variable (also called a response variable) are described or predicted
in terms of polynomial terms involving one or more independent or explanatory variables. An example of quadratic regression
in PROC GLM follows. These data are taken from Draper and Smith (1966, p. 57). Thirteen specimens of 90/10 Cu-Ni alloys are tested in a corrosion-wheel setup in order to examine corrosion. Each
specimen has a certain iron content. The wheel is rotated in salt sea water at 30 ft/sec for 60 days. Weight loss is used
to quantify the corrosion. The fe variable represents the iron content, and the loss variable denotes the weight loss in milligrams/square decimeter/day in the following DATA step.
title 'Regression in PROC GLM'; data iron; input fe loss @@; datalines; 0.01 127.6 0.48 124.0 0.71 110.8 0.95 103.9 1.19 101.5 0.01 130.1 0.48 122.0 1.44 92.3 0.71 113.1 1.96 83.7 0.01 128.0 1.44 91.4 1.96 86.2 ;
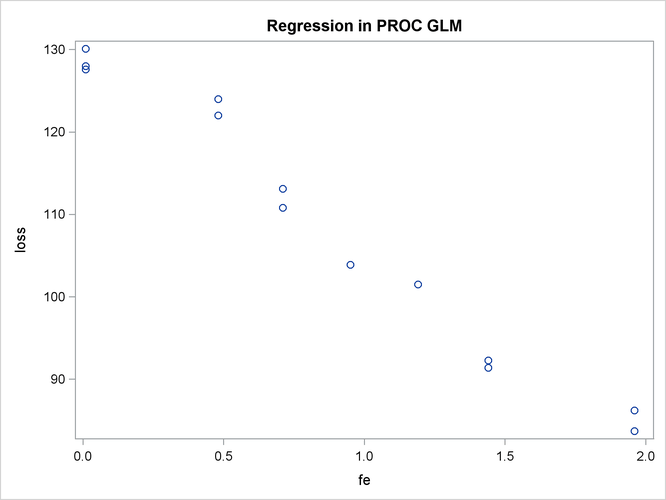
The SGSCATTER procedure is used in the following statements to request a scatter plot of the response variable versus the independent variable.
ods graphics on; proc sgscatter data=iron; plot loss*fe; run; ods graphics off;
The plot in Figure 44.4 displays a strong negative relationship between iron content and corrosion resistance, but it is not clear whether there is curvature in this relationship.
The following statements fit a quadratic regression model to the data. This enables you to estimate the linear relationship between iron content and corrosion resistance and to test for the presence of a quadratic component. The intercept is automatically fit unless the NOINT option is specified.
proc glm data=iron; model loss=fe fe*fe; run;
The CLASS statement is omitted because a regression line is being fitted. Unlike PROC REG, PROC GLM allows polynomial terms in the MODEL statement.
PROC GLM first displays preliminary information, shown in Figure 44.5, telling you that the GLM procedure has been invoked and stating the number of observations in the data set. If the model involves classification variables, they are also listed here, along with their levels.
Figure 44.5: Data Information
| Regression in PROC GLM |
| Number of Observations Read | 13 |
|---|---|
| Number of Observations Used | 13 |
Figure 44.6 shows the overall ANOVA table and some simple statistics. The degrees of freedom can be used to check that the model is correct and that the data have been read correctly. The Model degrees of freedom for a regression is the number of parameters in the model minus 1. You are fitting a model with three parameters in this case,
so the degrees of freedom are ![]() . The Corrected Total degrees of freedom are always one less than the number of observations used in the analysis.
. The Corrected Total degrees of freedom are always one less than the number of observations used in the analysis.
Figure 44.6: ANOVA Table
| Regression in PROC GLM |
| Source | DF | Sum of Squares | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| Model | 2 | 3296.530589 | 1648.265295 | 164.68 | <.0001 |
| Error | 10 | 100.086334 | 10.008633 | ||
| Corrected Total | 12 | 3396.616923 |
| R-Square | Coeff Var | Root MSE | loss Mean |
|---|---|---|---|
| 0.970534 | 2.907348 | 3.163642 | 108.8154 |
The R square indicates that the model accounts for 97% of the variation in LOSS. The coefficient of variation (Coeff Var), Root MSE (Mean Square for Error), and mean of the dependent variable are also listed.
The overall F test is significant ![]() , indicating that the model as a whole accounts for a significant amount of the variation in LOSS. Thus, it is appropriate
to proceed to testing the effects.
, indicating that the model as a whole accounts for a significant amount of the variation in LOSS. Thus, it is appropriate
to proceed to testing the effects.
Figure 44.7 contains tests of effects and parameter estimates. The latter are displayed by default when the model contains only continuous variables.
Figure 44.7: Tests of Effects and Parameter Estimates
| Source | DF | Type I SS | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| fe | 1 | 3293.766690 | 3293.766690 | 329.09 | <.0001 |
| fe*fe | 1 | 2.763899 | 2.763899 | 0.28 | 0.6107 |
| Source | DF | Type III SS | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| fe | 1 | 356.7572421 | 356.7572421 | 35.64 | 0.0001 |
| fe*fe | 1 | 2.7638994 | 2.7638994 | 0.28 | 0.6107 |
| Parameter | Estimate | Standard Error | t Value | Pr > |t| |
|---|---|---|---|---|
| Intercept | 130.3199337 | 1.77096213 | 73.59 | <.0001 |
| fe | -26.2203900 | 4.39177557 | -5.97 | 0.0001 |
| fe*fe | 1.1552018 | 2.19828568 | 0.53 | 0.6107 |
The t tests provided are equivalent to the Type III F tests. The quadratic term is not significant (p = 0.6107) and thus can be removed from the model; the linear term is significant ![]() . This suggests that there is indeed a straight-line relationship between
. This suggests that there is indeed a straight-line relationship between loss and fe.
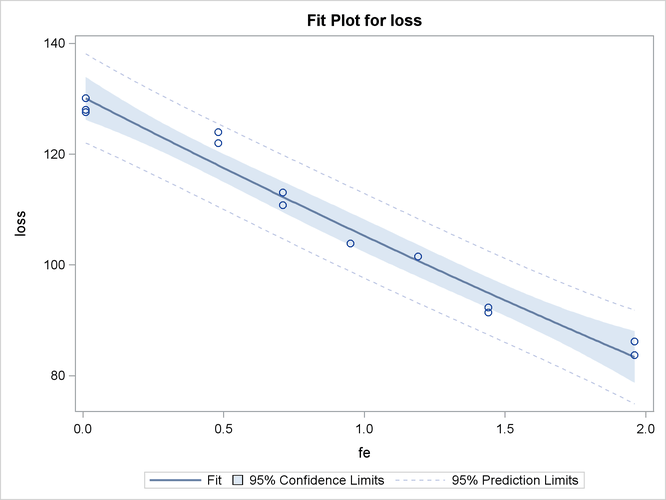
Finally, if ODS Graphics is enabled, PROC GLM also displays by default a scatter plot of the original data, as in Figure 44.4, with the quadratic fit overlaid. The following statements, which are the same as the previous analysis but with ODS Graphics enabled, additionally produce Figure 44.8.
ods graphics on; proc glm data=iron; model loss=fe fe*fe; run; ods graphics off;
The insignificance of the quadratic term in the model is reflected in the fact that the fit is nearly linear.
Fitting the model without the quadratic term provides more accurate estimates for ![]() and
and ![]() . PROC GLM allows only one MODEL statement per invocation of the procedure, so the PROC GLM statement must be issued again. The following statements are used to fit the linear model.
. PROC GLM allows only one MODEL statement per invocation of the procedure, so the PROC GLM statement must be issued again. The following statements are used to fit the linear model.
proc glm data=iron; model loss=fe; run;
Figure 44.9 displays the output produced by these statements. The linear term is still significant ![]() . The estimated model is now
. The estimated model is now
Figure 44.9: Linear Model Output
| Regression in PROC GLM |
| Source | DF | Sum of Squares | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| Model | 1 | 3293.766690 | 3293.766690 | 352.27 | <.0001 |
| Error | 11 | 102.850233 | 9.350021 | ||
| Corrected Total | 12 | 3396.616923 |
| R-Square | Coeff Var | Root MSE | loss Mean |
|---|---|---|---|
| 0.969720 | 2.810063 | 3.057780 | 108.8154 |
| Source | DF | Type I SS | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| fe | 1 | 3293.766690 | 3293.766690 | 352.27 | <.0001 |
| Source | DF | Type III SS | Mean Square | F Value | Pr > F |
|---|---|---|---|---|---|
| fe | 1 | 3293.766690 | 3293.766690 | 352.27 | <.0001 |
| Parameter | Estimate | Standard Error | t Value | Pr > |t| |
|---|---|---|---|---|
| Intercept | 129.7865993 | 1.40273671 | 92.52 | <.0001 |
| fe | -24.0198934 | 1.27976715 | -18.77 | <.0001 |