The LOGISTIC Procedure

Iterative Algorithms for Model Fitting

Subsections:

Iteratively Reweighted Least Squares Algorithm (Fisher Scoring)
Newton-Raphson Algorithm
Firth’s Bias-Reducing Penalized Likelihood

Two iterative maximum likelihood algorithms are available in PROC LOGISTIC for fitting an unconditional logistic regression, and these two methods are discussed in this section. For conditional logistic regression and models with the UNEQUALSLOPES specification, see the section NLOPTIONS Statement for details about available optimization techniques. Exact logistic regression uses a special algorithm described in the section Exact Conditional Logistic Regression.

The default maximum likelihood algorithm is the Fisher scoring method, which is equivalent to fitting by iteratively reweighted least squares. The alternative algorithm is the Newton-Raphson method. Both algorithms give the same parameter estimates; however, the estimated covariance matrix of the parameter estimators can differ slightly. This is due to the fact that Fisher scoring is based on the expected information matrix while the Newton-Raphson method is based on the observed information matrix. In the case of a binary logit model, the observed and expected information matrices are identical, resulting in identical estimated covariance matrices for both algorithms. You can specify the TECHNIQUE= option to select a fitting algorithm, and specify the FIRTH option to perform a bias-reducing penalized maximum likelihood fit. Note for generalized logit models that only the Newton-Raphson technique is available.

Iteratively Reweighted Least Squares Algorithm (Fisher Scoring)

Consider the multinomial variable $\bZ _ j=(Z_{1j},\ldots ,Z_{k+1,j})’$ such that

$\begin{eqnarray*} Z_{ij}= & \left\{ \begin{array}{ll} 1 & \mbox{if } Y_ j=i \\ 0 & \mbox{otherwise} \end{array} \right. \\ \end{eqnarray*}$

With $\pi _{ij}$ denoting the probability that the jth observation has response value i, the expected value of $\bZ _ j$ is $\bpi _ j=(\pi _{1j},\ldots ,\pi _{k+1,j})^\prime$ where $\pi _{k+1,j}=1-\sum _{i=1}^ k\pi _{ij}$ . The covariance matrix of $\bZ _ j$ is $\bV _ j$ , which is the covariance matrix of a multinomial random variable for one trial with parameter vector $\bpi _ j$ . Let $\bbeta$ be the vector of regression parameters; in other words, $\bbeta = (\alpha _{1}, \ldots , \alpha _{k}, \beta _{1},\ldots ,\beta _{s})’$ . Let $\bD _ j$ be the matrix of partial derivatives of $\bpi _ j$ with respect to $\bbeta$ . The estimating equation for the regression parameters is

$\sum _ j\bD ’_ j\bW _ j(\bZ _ j-\bpi _ j)=\bm {0}$

where ${\bW }_ j=w_ j f_ j {\bV }_ j^-$ , $w_ j$ and $f_ j$ are the weight and frequency of the jth observation, and ${\bV }_ j^-$ is a generalized inverse of ${\bV }_ j$ . PROC LOGISTIC chooses ${\bV }_ j^-$ as the inverse of the diagonal matrix with $\bpi _ j$ as the diagonal.

With a starting value of $\bbeta ^{(0)}$ , the maximum likelihood estimate of $\bbeta$ is obtained iteratively as

$\bbeta ^{(m+1)}=\bbeta ^{(m)}+(\sum _ j \bD ’_ j\bW _ j\bD _ j)^{-1} \sum _ j\bD ’_ j\bW _ j(\bZ _ j-\bpi _ j)$

where $\bD _ j$ , $\bW _ j$ , and $\bpi _ j$ are evaluated at $\bbeta ^{(m)}$ . The expression after the plus sign is the step size. If the likelihood evaluated at $\bbeta ^{(m+1)}$ is less than that evaluated at $\bbeta ^{(m)}$ , then $\bbeta ^{(m+1)}$ is recomputed by step-halving or ridging as determined by the value of the RIDGING= option. The iterative scheme continues until convergence is obtained—that is, until $\bbeta ^{(m+1)}$ is sufficiently close to $\bbeta ^{(m)}$ . Then the maximum likelihood estimate of $\bbeta$ is ${\widehat{\bbeta }}=\bbeta ^{(m+1)}$ .

The covariance matrix of ${\widehat{\bbeta }}$ is estimated by

$\widehat{\mbox{Cov}}({\widehat{\bbeta }})=(\sum _ j \widehat{\bD }’_ j\widehat{\bW }_ j\widehat{\bD }_ j)^{-1}=\widehat{\bI }^{-1}$

where $\widehat{\bD }_ j$ and $\widehat{\bW }_ j$ are, respectively, $\bD _ j$ and $\bW _ j$ evaluated at ${\widehat{\bbeta }}$ . $\widehat{\bI }$ is the information matrix, or the negative expected Hessian matrix, evaluated at ${\widehat{\bbeta }}$ .

By default, starting values are zero for the slope parameters, and for the intercept parameters, starting values are the observed cumulative logits (that is, logits of the observed cumulative proportions of response). Alternatively, the starting values can be specified with the INEST= option.

Newton-Raphson Algorithm

For cumulative models, let the parameter vector be $\bbeta =(\alpha _{1}, \dots ,\alpha _{k}, \beta _{1}, \dots ,\beta _{s})’$ , and for the generalized logit model let $\bbeta =(\alpha _{1}, \ldots ,\alpha _{k}, \bbeta _{1}’,\ldots , \bbeta _{k}’)’$ . The gradient vector and the Hessian matrix are given, respectively, by

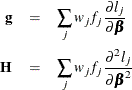
$\begin{eqnarray*} \mb {g} & = & \sum _ j w_ jf_ j\frac{\partial l_ j}{\partial \bbeta } \\ \bH & = & \sum _ j w_ jf_ j\frac{\partial ^2 l_ j}{\partial \bbeta ^2} \end{eqnarray*}$

where $l_ j=\log L_ j$ is the log likelihood for the jth observation. With a starting value of $\bbeta ^{(0)}$ , the maximum likelihood estimate ${\widehat{\bbeta }}$ of $\bbeta$ is obtained iteratively until convergence is obtained:

$\bbeta ^{(m+1)} = \bbeta ^{(m)} - \bH ^{-1}\mb {g}$

where $\bH$ and $\mb {g}$ are evaluated at $\bbeta ^{(m)}$ . If the likelihood evaluated at $\bbeta ^{(m+1)}$ is less than that evaluated at $\bbeta ^{(m)}$ , then $\bbeta ^{(m+1)}$ is recomputed by step-halving or ridging.

The covariance matrix of ${\widehat{\bbeta }}$ is estimated by

$\widehat{\mbox{Cov}}({\widehat{\bbeta }})= \widehat{\bI }^{-1}$

where the observed information matrix $\widehat{\bI }=-\widehat{\bH }$ is computed by evaluating $\bH$ at ${\widehat{\bbeta }}$ .

Firth’s Bias-Reducing Penalized Likelihood

Firth’s method is currently available only for binary logistic models. It replaces the usual score (gradient) equation

$g(\beta _ j) = \sum _{i=1}^ n (y_ i-\pi _ i)x_{ij} = 0 \quad (j=1,\ldots ,p)$

where p is the number of parameters in the model, with the modified score equation

$g(\beta _ j)^* = \sum _{i=1}^ n \{ y_ i-\pi _ i +h_ i(0.5-\pi _ i)\} x_{ij} = 0 \quad (j=1,\ldots ,p)$

where the $h_ i$ s are the ith diagonal elements of the hat matrix $\bW ^{1/2}\bX (\bX ’\bW \bX )^{-1}\bX ’\bW ^{1/2}$ and $\bW = \mbox{diag}\{ \pi _ i(1-\pi _ i)\}$ . The Hessian matrix is not modified by this penalty, and the optimization method is performed in the usual manner.