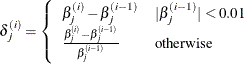-
ABSFCONV=value
-
specifies the absolute function convergence criterion. Convergence requires a small change in the log-likelihood function
in subsequent iterations,
where 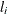 is the value of the log-likelihood function at iteration i.
is the value of the log-likelihood function at iteration i.
By default, ABSFCONV=1E–12. You can also specify the FCONV= and XCONV= criteria; optimizations are terminated as soon as one criterion is satisfied.
-
ADDTOBS
-
adds the observed sufficient statistic to the sampled exact distribution if the statistic was not sampled. This option has
no effect unless the METHOD=NETWORKMC option is specified and the ESTIMATE option is specified in the EXACT statement. If the observed statistic has not been sampled, then the parameter estimate does not exist; by specifying this
option, you can produce (biased) estimates.
-
BUILDSUBSETS
-
builds every distribution for sampling. By default, some exact distributions are created by taking a subset of a previously
generated exact distribution. When the METHOD=NETWORKMC option is invoked, this subsetting behavior has the effect of using fewer than the desired n samples; see the N= option for more details. Use the BUILDSUBSETS option to suppress this subsetting.
-
EPSILON=value
-
controls how the partial sums 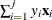 are compared. value must be between 0 and 1; by default, value=1E–8.
are compared. value must be between 0 and 1; by default, value=1E–8.
-
FCONV=value
-
specifies the relative function convergence criterion. Convergence requires a small relative change in the log-likelihood
function in subsequent iterations,
where 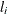 is the value of the log likelihood at iteration i.
is the value of the log likelihood at iteration i.
By default, FCONV=1E–8. You can also specify the ABSFCONV= and XCONV= criteria; if more than one criterion is specified, then optimizations are terminated as soon as one criterion is satisfied.
-
MAXTIME=seconds
-
specifies the maximum clock time (in seconds) that PROC LOGISTIC can use to calculate the exact distributions. If the limit
is exceeded, the procedure halts all computations and prints a note to the LOG. The default maximum clock time is seven days.
-
METHOD=keyword
-
specifies which exact conditional algorithm to use for every EXACT statement specified. You can specify one of the following keywords:
- DIRECT
-
invokes the multivariate shift algorithm of Hirji, Mehta, and Patel (1987). This method directly builds the exact distribution, but it can require an excessive amount of memory in its intermediate
stages. METHOD=DIRECT is invoked by default when you are conditioning out at most the intercept, or when the LINK=GLOGIT option is specified in the MODEL statement.
- NETWORK
-
invokes an algorithm described in Mehta, Patel, and Senchaudhuri (1992). This method builds a network for each parameter that you are conditioning out, combines the networks, then uses the multivariate
shift algorithm to create the exact distribution. The NETWORK method can be faster and require less memory than the DIRECT
method. The NETWORK method is invoked by default for most analyses.
- NETWORKMC
-
invokes the hybrid network and Monte Carlo algorithm of Mehta, Patel, and Senchaudhuri (1992). This method creates a network, then samples from that network; this method does not reject any of the samples at the cost
of using a large amount of memory to create the network. METHOD=NETWORKMC is most useful for producing parameter estimates
for problems that are too large for the DIRECT and NETWORK methods to handle and for which asymptotic methods are invalid—for
example, for sparse data on a large grid.
-
N=n
-
specifies the number of Monte Carlo samples to take when the METHOD=NETWORKMC option is specified. By default, n = 10,000. If the procedure cannot obtain n samples due to a lack of memory, then a note is printed in the SAS log (the number of valid samples is also reported in the
listing) and the analysis continues.
The number of samples used to produce any particular statistic might be smaller than n. For example, let X1 and X2 be continuous variables, denote their joint distribution by f(X1,X2), and let f(X1 | X2 = x2) denote the marginal distribution of X1 conditioned on the observed value of X2. If you request the JOINT test of X1 and X2, then n samples are used to generate the estimate 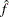 (X1,X2) of f(X1,X2), from which the test is computed. However, the parameter estimate for X1 is computed from the subset of
(X1,X2) of f(X1,X2), from which the test is computed. However, the parameter estimate for X1 is computed from the subset of 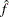 (X1,X2) that has X2 = x2, and this subset need not contain n samples. Similarly, the distribution for each level of a classification variable is created by extracting the appropriate
subset from the joint distribution for the CLASS variable.
(X1,X2) that has X2 = x2, and this subset need not contain n samples. Similarly, the distribution for each level of a classification variable is created by extracting the appropriate
subset from the joint distribution for the CLASS variable.
In some cases, the marginal sample size can be too small to admit accurate estimation of a particular statistic; a note is
printed in the SAS log when a marginal sample size is less than 100. Increasing n increases the number of samples used in a marginal distribution; however, if you want to control the sample size exactly,
you can either specify the BUILDSUBSETS option or do both of the following:
-
Remove the JOINT option from the EXACT statement.
-
Create dummy variables in a DATA step to represent the levels of a CLASS variable, and specify them as independent variables in the MODEL statement.
-
NOLOGSCALE
-
specifies that computations for the exact conditional models be computed by using normal scaling. Log scaling can handle numerically
larger problems than normal scaling; however, computations in the log scale are slower than computations in normal scale.
-
ONDISK
-
uses disk space instead of random access memory to build the exact conditional distribution. Use this option to handle larger
problems at the cost of slower processing.
-
SEED=seed
-
specifies the initial seed for the random number generator used to take the Monte Carlo samples when the METHOD=NETWORKMC option is specified. The value of the SEED= option must be an integer. If you do not specify a seed, or if you specify a
value less than or equal to zero, then PROC LOGISTIC uses the time of day from the computer’s clock to generate an initial
seed.
-
STATUSN=number
-
prints a status line in the SAS log after every number of Monte Carlo samples when the METHOD=NETWORKMC option is specified. The number of samples taken and the current exact p-value for testing the significance of the model are displayed. You can use this status line to track the progress of the
computation of the exact conditional distributions.
-
STATUSTIME=seconds
-
specifies the time interval (in seconds) for printing a status line in the LOG. You can use this status line to track the
progress of the computation of the exact conditional distributions. The time interval you specify is approximate; the actual
time interval varies. By default, no status reports are produced.
-
XCONV=value
-
specifies the relative parameter convergence criterion. Convergence requires a small relative parameter change in subsequent
iterations,
where
and 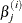 is the estimate of the jth parameter at iteration i.
is the estimate of the jth parameter at iteration i.
By default, XCONV=1E–4. You can also specify the ABSFCONV= and FCONV= criteria; if more than one criterion is specified, then optimizations are terminated as soon as one criterion is satisfied.
 PROC LOGISTIC StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementEFFECT StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementODDSRATIO StatementOUTPUT StatementROC StatementROCCONTRAST StatementSCORE StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement
PROC LOGISTIC StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementEFFECT StatementEFFECTPLOT StatementESTIMATE StatementEXACT StatementEXACTOPTIONS StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementODDSRATIO StatementOUTPUT StatementROC StatementROCCONTRAST StatementSCORE StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement Missing ValuesResponse Level OrderingLink Functions and the Corresponding DistributionsDetermining Observations for Likelihood ContributionsIterative Algorithms for Model FittingConvergence CriteriaExistence of Maximum Likelihood EstimatesEffect-Selection MethodsModel Fitting InformationGeneralized Coefficient of DeterminationScore Statistics and TestsConfidence Intervals for ParametersOdds Ratio EstimationRank Correlation of Observed Responses and Predicted ProbabilitiesLinear Predictor, Predicted Probability, and Confidence LimitsClassification TableOverdispersionThe Hosmer-Lemeshow Goodness-of-Fit TestReceiver Operating Characteristic CurvesTesting Linear Hypotheses about the Regression CoefficientsRegression DiagnosticsScoring Data SetsConditional Logistic RegressionExact Conditional Logistic RegressionInput and Output Data SetsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics
Missing ValuesResponse Level OrderingLink Functions and the Corresponding DistributionsDetermining Observations for Likelihood ContributionsIterative Algorithms for Model FittingConvergence CriteriaExistence of Maximum Likelihood EstimatesEffect-Selection MethodsModel Fitting InformationGeneralized Coefficient of DeterminationScore Statistics and TestsConfidence Intervals for ParametersOdds Ratio EstimationRank Correlation of Observed Responses and Predicted ProbabilitiesLinear Predictor, Predicted Probability, and Confidence LimitsClassification TableOverdispersionThe Hosmer-Lemeshow Goodness-of-Fit TestReceiver Operating Characteristic CurvesTesting Linear Hypotheses about the Regression CoefficientsRegression DiagnosticsScoring Data SetsConditional Logistic RegressionExact Conditional Logistic RegressionInput and Output Data SetsComputational ResourcesDisplayed OutputODS Table NamesODS Graphics Stepwise Logistic Regression and Predicted ValuesLogistic Modeling with Categorical PredictorsOrdinal Logistic RegressionNominal Response Data: Generalized Logits ModelStratified SamplingLogistic Regression DiagnosticsROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence LimitsComparing Receiver Operating Characteristic CurvesGoodness-of-Fit Tests and SubpopulationsOverdispersionConditional Logistic Regression for Matched Pairs DataFirth’s Penalized Likelihood Compared with Other ApproachesComplementary Log-Log Model for Infection RatesComplementary Log-Log Model for Interval-Censored Survival TimesScoring Data SetsUsing the LSMEANS StatementPartial Proportional Odds Model
Stepwise Logistic Regression and Predicted ValuesLogistic Modeling with Categorical PredictorsOrdinal Logistic RegressionNominal Response Data: Generalized Logits ModelStratified SamplingLogistic Regression DiagnosticsROC Curve, Customized Odds Ratios, Goodness-of-Fit Statistics, R-Square, and Confidence LimitsComparing Receiver Operating Characteristic CurvesGoodness-of-Fit Tests and SubpopulationsOverdispersionConditional Logistic Regression for Matched Pairs DataFirth’s Penalized Likelihood Compared with Other ApproachesComplementary Log-Log Model for Infection RatesComplementary Log-Log Model for Interval-Censored Survival TimesScoring Data SetsUsing the LSMEANS StatementPartial Proportional Odds Model