The MCMC Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 How PROC MCMC WorksBlocking of ParametersSampling MethodsTuning the Proposal DistributionDirect SamplingConjugate SamplingInitial Values of the Markov ChainsAssignments of ParametersStandard DistributionsUsage of Multivariate DistributionsSpecifying a New DistributionUsing Density Functions in the Programming StatementsTruncation and CensoringSome Useful SAS FunctionsMatrix Functions in PROC MCMCCreate Design MatrixModeling Joint LikelihoodRegenerating Diagnostics PlotsCaterpillar PlotAutocall Macros for PostprocessingGamma and Inverse-Gamma DistributionsPosterior Predictive DistributionHandling of Missing DataFunctions of Random-Effects ParametersFloating Point Errors and OverflowsHandling Error MessagesComputational ResourcesDisplayed OutputODS Table NamesODS Graphics
How PROC MCMC WorksBlocking of ParametersSampling MethodsTuning the Proposal DistributionDirect SamplingConjugate SamplingInitial Values of the Markov ChainsAssignments of ParametersStandard DistributionsUsage of Multivariate DistributionsSpecifying a New DistributionUsing Density Functions in the Programming StatementsTruncation and CensoringSome Useful SAS FunctionsMatrix Functions in PROC MCMCCreate Design MatrixModeling Joint LikelihoodRegenerating Diagnostics PlotsCaterpillar PlotAutocall Macros for PostprocessingGamma and Inverse-Gamma DistributionsPosterior Predictive DistributionHandling of Missing DataFunctions of Random-Effects ParametersFloating Point Errors and OverflowsHandling Error MessagesComputational ResourcesDisplayed OutputODS Table NamesODS Graphics -
Examples
 Simulating Samples From a Known DensityBox-Cox TransformationLogistic Regression Model with a Diffuse PriorLogistic Regression Model with Jeffreys’ PriorPoisson RegressionNonlinear Poisson Regression ModelsLogistic Regression Random-Effects ModelNonlinear Poisson Regression Multilevel Random-Effects ModelMultivariate Normal Random-Effects ModelMissing at Random AnalysisNonignorably Missing Data (MNAR) AnalysisChange Point ModelsExponential and Weibull Survival AnalysisTime Independent Cox ModelTime Dependent Cox ModelPiecewise Exponential Frailty ModelNormal Regression with Interval CensoringConstrained AnalysisImplement a New Sampling AlgorithmUsing a Transformation to Improve MixingGelman-Rubin Diagnostics
Simulating Samples From a Known DensityBox-Cox TransformationLogistic Regression Model with a Diffuse PriorLogistic Regression Model with Jeffreys’ PriorPoisson RegressionNonlinear Poisson Regression ModelsLogistic Regression Random-Effects ModelNonlinear Poisson Regression Multilevel Random-Effects ModelMultivariate Normal Random-Effects ModelMissing at Random AnalysisNonignorably Missing Data (MNAR) AnalysisChange Point ModelsExponential and Weibull Survival AnalysisTime Independent Cox ModelTime Dependent Cox ModelPiecewise Exponential Frailty ModelNormal Regression with Interval CensoringConstrained AnalysisImplement a New Sampling AlgorithmUsing a Transformation to Improve MixingGelman-Rubin Diagnostics - References
The following simple example illustrates the usage of the multivariate distributions in PROC MCMC. Suppose you are interested in estimating the mean and covariance of multivariate data using this multivariate normal model:
where
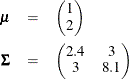
You can use the following independent prior on ![]() and
and ![]() :
:
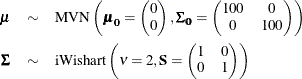
The following IML procedure statements simulate 100 random multivariate normal samples:
title 'An Example that Uses Multivariate Distributions';
proc iml;
N = 100;
Mean = {1 2};
Cov = {2.4 3, 3 8.1};
call randseed(1);
x = RANDNORMAL( N, Mean, Cov );
SampleMean = x[:,];
n = nrow(x);
y = x - repeat( SampleMean, n );
SampleCov = y`*y / (n-1);
print SampleMean Mean, SampleCov Cov;
cname = {"x1", "x2"};
create inputdata from x [colname = cname];
append from x;
close inputdata;
quit;
Figure 61.13 prints the sample mean and covariance of the simulated data, in addition to the true mean and covariance matrix.
The following PROC MCMC statements estimate the posterior mean and covariance of the multivariate normal data:
proc mcmc data=inputdata seed=17 nmc=3000 diag=none; ods select PostSumInt; array data[2] x1 x2; array mu[2]; array Sigma[2,2]; array mu0[2] (0 0); array Sigma0[2,2] (100 0 0 100); array S[2,2] (1 0 0 1); parm mu Sigma; prior mu ~ mvn(mu0, Sigma0); prior Sigma ~ iwish(2, S); model data ~ mvn(mu, Sigma); run;
To use the multivariate distribution, you must specify parameters (or random variables in the MODEL statement) in an array
form. The first ARRAY
statement creates an one-dimensional array data, which contains two numeric variables, x1 and x2, from the input data set. The data variable is your response variable. The subsequent statements defines two array-parameters (mu and Sigma) and three constant array-hyperparameters (mu0, Sigma0, and S). The PARMS
statement declares mu and Sigma to be model parameters. The two PRIOR
statements specify the multivariate normal and inverse Wishart distributions as the prior for mu and Sigma, respectively. The MODEL
statement specifies the multivariate normal likelihood with data as the random variable, mu as the mean, and Sigma as the covariance matrix.
Figure 61.14 lists the estimated posterior statistics for the parameters.
Figure 61.14: Estimated Mean and Covariance
| Posterior Summaries and Intervals | |||||
|---|---|---|---|---|---|
| Parameter | N | Mean | Standard Deviation |
95% HPD Interval | |
| mu1 | 3000 | 0.9941 | 0.1763 | 0.6338 | 1.3106 |
| mu2 | 3000 | 2.1135 | 0.3112 | 1.4939 | 2.7165 |
| Sigma1 | 3000 | 2.8726 | 0.4084 | 2.1001 | 3.6723 |
| Sigma2 | 3000 | 3.7573 | 0.6418 | 2.5791 | 5.0223 |
| Sigma3 | 3000 | 3.7573 | 0.6418 | 2.5791 | 5.0223 |
| Sigma4 | 3000 | 9.3987 | 1.3224 | 7.0155 | 12.0969 |