The MCMC Procedure

Floating Point Errors and Overflows

Subsections:

Problems Evaluating Code for Objective Function
Long Run Times
Slow or No Convergence
Precision of Solution

When performing a Markov chain Monte Carlo simulation, you must calculate a proposed jump and an objective function (usually a posterior density). These calculations might lead to arithmetic exceptions and overflows. A typical cause of these problems is parameters with widely varying scales. If the posterior variances of your parameters vary by more than a few orders of magnitude, the numerical stability of the optimization problem can be severely reduced and can result in computational difficulties. A simple remedy is to rescale all the parameters so that their posterior variances are all approximately equal. Changing the SCALE= option might help if the scale of your parameters is much different than one. Another source of numerical instability is highly correlated parameters. Often a model can be reparameterized to reduce the posterior correlations between parameters.

If parameter rescaling does not help, consider the following actions:

provide different initial values or try a different seed value
use boundary constraints to avoid the region where overflows might happen
change the algorithm (specified in programming statements) that computes the objective function

Problems Evaluating Code for Objective Function

The initial values must define a point for which the programming statements can be evaluated. However, during simulation, the algorithm might iterate to a point where the objective function cannot be evaluated. If you program your own likelihood, priors, and hyperpriors by using SAS statements and the GENERAL function in the MODEL , PRIOR , AND HYPERPRIOR statements, you can specify that an expression cannot be evaluated by setting the value you pass back through the GENERAL function to missing. This tells the PROC MCMC that the proposed set of parameters is invalid, and the proposal will not be accepted. If you use the shorthand notation that the MODEL , PRIOR , AND HYPERPRIOR statements provide, this error checking is done for you automatically.

Long Run Times

PROC MCMC can take a long time to run for problems with complex models, many parameters, or large input data sets. Although the techniques used by PROC MCMC are some of the best available, they are not guaranteed to converge or proceed quickly for all problems. Ill-posed or misspecified models can cause the algorithms to use more extensive calculations designed to achieve convergence, and this can result in longer run times. You should make sure that your model is specified correctly, that your parameters are scaled to the same order of magnitude, and that your data reasonably match the model that you are specifying.

To speed general computations, you should check over your programming statements to minimize the number of unnecessary operations. For example, you can use the proportional kernel in the priors or the likelihood and not add constants in the densities. You can also use the BEGINCNST and ENDCNST to reduce unnecessary computations on constants, and the BEGINNODATA and ENDNODATA statements to reduce observation-level calculations.

Reducing the number of blocks (the number of the PARMS statements) can speed up the sampling process. A single-block program is approximately three times faster than a three-block program for the same number of iterations. On the other hand, you do not want to put too many parameters in a single block, because blocks with large size tend not to produce well-mixed Markov chains.

If some parameters satisfy the conditional independence assumption, such as in the random-effects models or latent variable models, consider using the RANDOM statement to model these parameters. This statement takes advantage of the conditional independence assumption and can sample a larger number of parameters at a more efficient pace.

Slow or No Convergence

If the simulator is slow or fails to converge, you can try changing the model as follows:

Change the number of Monte Carlo iterations (NMC= ), or the number of burn-in iterations (NBI= ), or both. Perhaps the chain just needs to run a little longer. Note that after the simulation, you can always use the DATA step or the FIRSTOBS data set option to throw away initial observations where the algorithm has not yet burned in, so it is not always necessary to set NBI= to a large value.
Increase the number of tuning. The proposal tuning can often work better in large models (models that have more parameters) with larger values of NTU= . The idea of tuning is to find a proposal distribution that is a good approximation to the posterior distribution. Sometimes 500 iterations per tuning phase (the default) is not sufficient to find a good approximating covariance.
Change the initial values to more feasible starting values. Sometimes the proposal tuning starts badly if the initial values are too far away from the main mass of the posterior density, and it might not be able to recover.
Use the PROPCOV= option to start the Markov chain at better starting values. With the PROPCOV=QUANEW option, PROC MCMC optimizes the object function and uses the posterior mode as the starting value of the Markov chain. In addition, a quadrature approximation to the posterior mode is used as the proposal covariance matrix. This option works well in many cases and can improve the mixing of the chain and shorten the tuning and burn-in time.
Parameterize your model to include conjugacy, such as using the gamma prior on the precision parameter in a normal distribution or using an inverse gamma on the variance parameter. For a list of conjugate sampling methods that PROC MCMC supports, see the section Conjugate Sampling.
Change the blocking by using the PARMS statements. Sometimes poor mixing and slow convergence can be attributed to highly correlated parameters being in different parameter blocks.
Modify the target acceptance rate. A target acceptance rate of about 25% works well for many multi-parameter problems, but if the mixing is slow, a lower target acceptance rate might be better.
Change the initial scaling or the TUNEWT= option to possibly help the proposal tuning.
Consider using a different proposal distribution. If from a trace plot you see that a chain traverses to the tail area and sometimes takes quite a few simulations before it comes back, you can consider using a t proposal distribution. You can do this by either using the PROC option PROPDIST=T or using a PARMS statement option T.
Transform parameters and sample on a different scale. For example, if a parameter has a gamma distribution, sample on the logarithm scale instead. A parameter a that has a gamma distribution is equivalent to 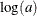$\log (a)$ that has an egamma distribution, with the same distribution specification. For example, the following two formulations are equivalent:
```
parm a;
prior a ~ gamma(shape = 0.001, scale = 0.001);
```
and
```
parm la;
prior la ~ egamma(shape = 0.001, scale = 0.001);
a = exp(la);
```
See Nonlinear Poisson Regression Models and Using a Transformation to Improve Mixing. You can also use the logit transformation on parameters that have uniform 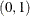$(0, 1)$ priors. This prior is often used on probability parameters. The logit transformation is as follows: 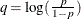$q = \log (\frac{p}{1-p})$ . The distribution on q is the Jacobian of the transformation: 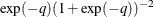$\exp (-q) (1+\exp (-q))^{-2}$ . Again, the following two formulations are equivalent:
```
parm p;
prior p ~ uniform(0, 1);
```
and
```
parm q;
lp = -q - 2 * log(1 + exp(-q));
prior q ~ general(lp);
p = 1/(1+exp(-q));
```

Precision of Solution

In some applications, PROC MCMC might produce parameter values that are not precise enough. Usually, this means that there were not enough iterations in the simulation. At best, the precision of MCMC estimates increases with the square of the simulation sample size. Autocorrelation in the parameter values deflate the precision of the estimates. For more information about autocorrelations in Markov chains, see the section Autocorrelations in Chapter 7: Introduction to Bayesian Analysis Procedures.