The MCMC Procedure

Example 61.20 Using a Transformation to Improve Mixing

Proper transformations of parameters can often improve the mixing in PROC MCMC. You already saw this in Nonlinear Poisson Regression Models, which sampled using the $\log$ scale of parameters that priors that are strictly positive, such as the gamma priors. This example shows another useful transformation: the logit transformation on parameters that take a uniform prior on [0, 1].

The data set is taken from Sharples (1990). It is used in Chaloner and Brant (1988) and Chaloner (1994) to identify outliers in the data set in a two-level hierarchical model. Congdon (2003) also uses this data set to demonstrates the same technique. This example uses the data set to illustrate how mixing can be improved using transformation and does not address the question of outlier detection as in those papers. The following statements create the data set:

data inputdata;
   input nobs grp y @@;
   ind = _n_;
   datalines;
1 1 24.80 2 1 26.90 3 1 26.65
4 1 30.93 5 1 33.77 6 1 63.31
1 2 23.96 2 2 28.92 3 2 28.19
4 2 26.16 5 2 21.34 6 2 29.46
1 3 18.30 2 3 23.67 3 3 14.47
4 3 24.45 5 3 24.89 6 3 28.95
1 4 51.42 2 4 27.97 3 4 24.76
4 4 26.67 5 4 17.58 6 4 24.29
1 5 34.12 2 5 46.87 3 5 58.59
4 5 38.11 5 5 47.59 6 5 44.67
;

There are five groups (grp, $j=1, \cdots , 5$ ) with six observations (nobs, $i=1, \cdots , 6$ ) in each. The two-level hierarchical model is specified as follows:

$\begin{eqnarray*} y_{ij} & \sim & \mbox{normal}(\theta _ j, \mbox{prec} = \tau _ w) \\ \theta _ j & \sim & \mbox{normal}(\mu , \mbox{prec} = \tau _ b) \\ \mu & \sim & \mbox{normal}(0, \mbox{prec} = 1e-6) \\ \tau & \sim & \mbox{gamma}(0.001, \mbox{iscale} = 0.001) \\ p & \sim & \mbox{uniform}(0, 1) \end{eqnarray*}$

with the precision parameters related to each other in the following way:

$\begin{eqnarray*} \tau _ b & =& \tau / p \\ \tau _ w & =& \tau _ b - \tau \end{eqnarray*}$

The total number of parameters in this model is eight: $\theta _1, \cdots , \theta _5, \mu , \tau$ , and p.

The following statements fit the model:

ods graphics on;
proc mcmc data=inputdata nmc=50000 thin=10 outpost=m1 seed=17
          plot=trace;
   ods select ess tracepanel;
   parms p;
   parms tau;
   parms mu;

   prior p ~ uniform(0,1);
   prior tau ~ gamma(shape=0.001,iscale=0.001);
   prior mu ~ normal(0,prec=0.00000001);
   beginnodata;
   taub = tau/p;
   tauw = taub-tau;
   endnodata;

   random theta ~ normal(mu, prec=taub) subject=grp monitor=(theta);
   model y ~ normal(theta,prec=tauw);
run;

The ODS SELECT statement displays the effective sample size table and the trace plots. The ODS GRAPHICS ON statement enables ODS Graphics. The PROC MCMC statement specifies the usual options for the procedure run and produces trace plots (PLOTS=TRACE ). The three PARMS statements put three model parameters, p, tau, and mu, in three different blocks. The PRIOR statements specify the prior distributions, and the programming statements enclosed with the BEGINNODATA and ENDNODATA statements calculate the transformation to taub and tauw. 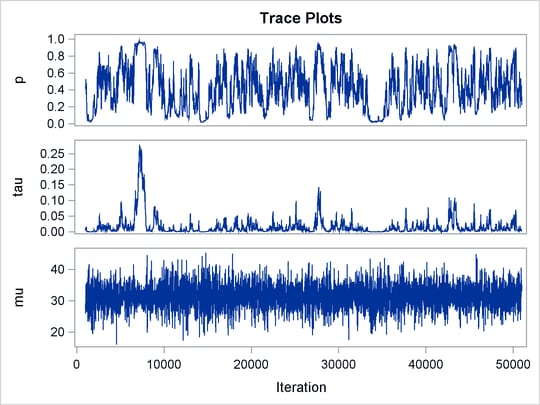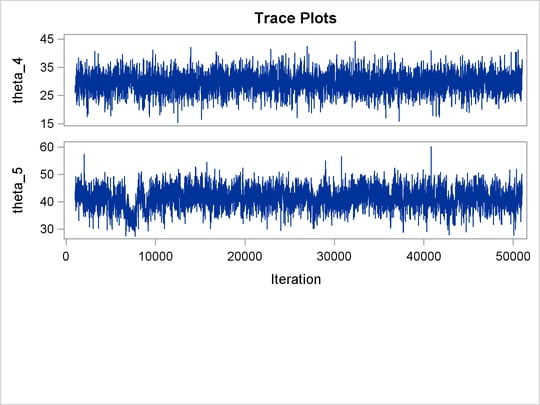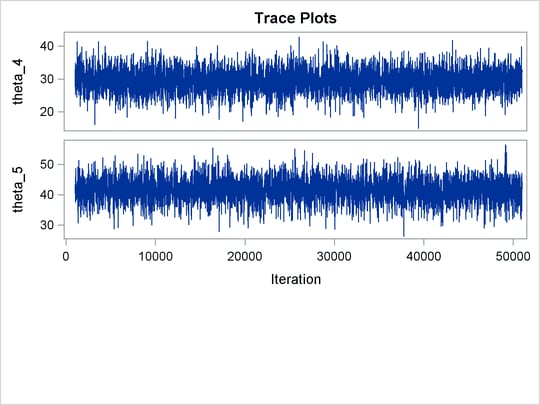The RANDOM statement specifies the random effect, its prior distribution, and the subject variable. The resulting trace plots are shown in Output 61.20.1, and the effective sample size table is shown in Output 61.20.2.

Output 61.20.1: Trace Plots

Output 61.20.2: Bad Effective Sample Sizes

Implement a New Sampling Algorithm

The MCMC Procedure

Effective Sample Sizes
Parameter	ESS	Autocorrelation Time	Efficiency
p	81.3	61.5342	0.0163
tau	61.2	81.7440	0.0122
mu	5000.0	1.0000	1.0000
theta_1	4839.9	1.0331	0.9680
theta_2	2739.7	1.8250	0.5479
theta_3	1346.6	3.7130	0.2693
theta_4	4897.5	1.0209	0.9795
theta_5	338.1	14.7866	0.0676

The trace plots show that most parameters have relatively good mixing. Two exceptions appear to be p and $\tau$ . The trace plot of p shows a slow periodic movement. The $\tau$ parameter does not have good mixing either. When the values are close to zero, the chain stays there for periods of time. An inspection of the effective sample sizes table reveals the same conclusion: p and $\tau$ have much smaller ESSs than the rest of the parameters.

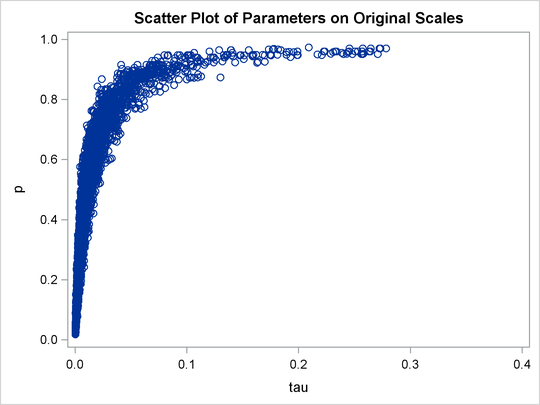
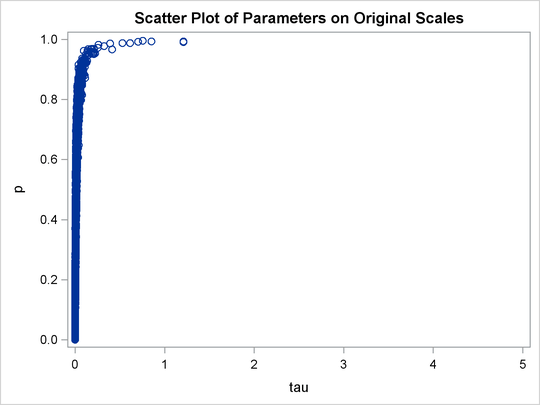
A scatter plot of the posterior samples of p and $\tau$ reveals why mixing is bad in these two dimensions. The following statements generate the scatter plot in Output 61.20.3:

title 'Scatter Plot of Parameters on Original Scales';

proc sgplot data=m1;
   yaxis label = 'p';
   xaxis label = 'tau' values=(0 to 0.4 by 0.1);
   scatter x = tau y = p;
run;

Output 61.20.3: Scatter Plot of $\tau$ versus p

The two parameters clearly have a nonlinear relationship. It is not surprising that the Metropolis algorithm does not work well here. The algorithm is designed for cases where the parameters are linearly related with each other.

To improve on mixing, you can sample on the log of $\tau$ , instead of sampling on $\tau$ . The formulation is:

$\begin{eqnarray*} \tau & \sim & \mbox{gamma}(\mbox{shape}=0.001, \mbox{iscale}=0.001) \\ \log (\tau ) & \sim & \mbox{egamma}(\mbox{shape}=0.001, \mbox{iscale}=0.001) \end{eqnarray*}$

See the section Standard Distributions for the definitions of the gamma and egamma distributions. In addition, you can sample on the logit of p. Note that

$p \sim \mbox{uniform}(0, 1)$

is equivalent to

${\Variable{lgp}} = \mbox{logit}(p) \sim \mbox{logistic}(0, 1)$

The following statements fit the same model by using transformed parameters:

proc mcmc data=inputdata nmc=50000 thin=10 outpost=m2 seed=17
          monitor=(p tau mu) plot=trace;
   ods select ess tracepanel;
   parms ltau lgp mu ;

   prior ltau ~ egamma(shape=0.001,iscale=0.001);
   prior lgp ~ logistic(0,1);
   prior mu ~ normal(0,prec=0.00000001);

   beginnodata;
   tau = exp(ltau);
   p = logistic(lgp);
   taub = tau/p;
   tauw = taub-tau;
   endnodata;

   random theta ~ normal(mu, prec=taub) subject=grp monitor=(theta);
   model y ~ normal(theta,prec=tauw);
run;

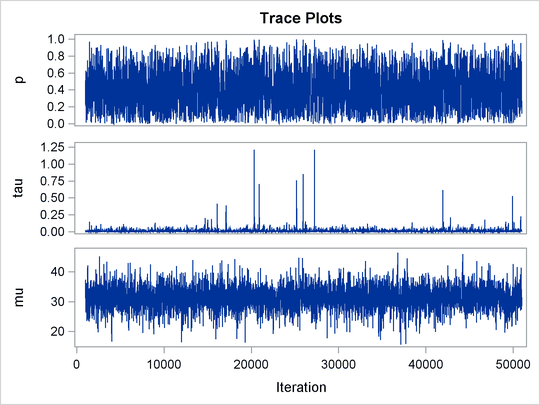
The variable lgp is the logit transformation of p, and ltau is the log transformation of $\tau$ . The prior for ltau is egamma , and the prior for lgp is logistic . The TAU and P assignment statements transform the parameters back to their original scales. The rest of the programs remain unchanged. Trace plots (Output 61.20.4) and effective sample size (Output 61.20.5) both show significant improvements in the mixing for both p and $\tau$ .

Output 61.20.4: Trace Plots after Transformation

Output 61.20.5: Effective Sample Sizes after Transformation

The MCMC Procedure

Effective Sample Sizes
Parameter	ESS	Autocorrelation Time	Efficiency
p	3119.4	1.6029	0.6239
tau	2588.0	1.9320	0.5176
mu	5000.0	1.0000	1.0000
theta_1	4866.0	1.0275	0.9732
theta_2	5244.5	0.9534	1.0489
theta_3	5000.0	1.0000	1.0000
theta_4	5000.0	1.0000	1.0000
theta_5	4054.8	1.2331	0.8110

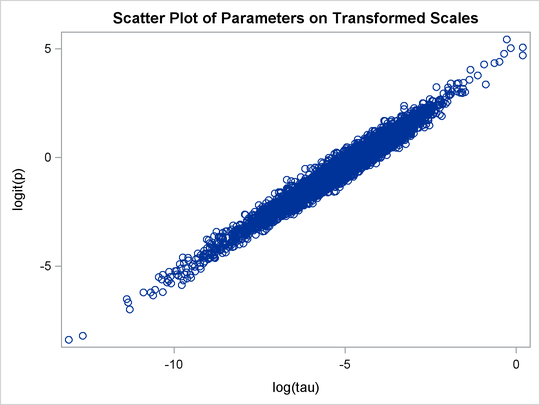
The following statements generate Output 61.20.6 and Output 61.20.7:

title 'Scatter Plot of Parameters on Transformed Scales';

proc sgplot data=m2;
   yaxis label = 'logit(p)';
   xaxis label = 'log(tau)';
   scatter x = ltau y = lgp;
run;

title 'Scatter Plot of Parameters on Original Scales';

proc sgplot data=m2;
   yaxis label = 'p';
   xaxis label = 'tau' values=(0 to 5.0 by 1);
   scatter x = tau y = p;
run;
ods graphics off;

Output 61.20.6: Scatter Plot of $\log (\tau )$ versus $\mbox{logit}(p)$ , After Transformation

Scatter Plot of () versus logit(p), After Transformation

Output 61.20.7: Scatter Plot of $\tau$ versus p, After Transformation

Scatter Plot of versus , After Transformation

The scatter plot of $\log (\tau )$ versus $\mbox{logit}(p)$ shows a linear relationship between the two transformed parameters, and this explains the improvement in mixing. In addition, the transformations also help the Markov chain better explore in the original parameter space. Output 61.20.7 shows a scatter plot of $\tau$ versus p. The plot is similar to Output 61.20.3. However, note that tau has a far longer tail in Output 61.20.7, extending all the way to 5 as opposed to 0.15 in Output 61.20.3. This means that the second Markov chain can explore this dimension of the parameter more efficiently, and as a result, you are able to draw more precise inference with an equal number of simulations.