The PRINCOMP Procedure

PROC PRINCOMP Statement

PROC PRINCOMP <options>;

The PROC PRINCOMP statement invokes the PRINCOMP procedure. Optionally, it also identifies input and output data sets, specifies the analyses that are performed, and controls displayed output. Table 79.1 summarizes the options available in the PROC PRINCOMP statement.

Table 79.1: Summary of PROC PRINCOMP Statement Options

Option	Description
Specify Data Sets
DATA=	Specifies the name of the input data set
OUT=	Specifies the name of the output data set
OUTSTAT=	Specifies the name of the output data set that contains various statistics
Specify Details of Analysis
COV	Computes the principal components from the covariance matrix
N=	Specifies the number of principal components to be computed
NOINT	Omits the intercept from the model
PREFIX=	Specifies a prefix for naming the principal components
PARPREFIX=	Specifies a prefix for naming the residual variables
SINGULAR=	Specifies the singularity criterion
STD	Standardizes the principal component scores
VARDEF=	Specifies the divisor used in calculating variances and standard deviations
Suppress the Display of Output
NOPRINT	Suppresses the display of all output
Specify ODS Graphics Details
PLOTS=	Specifies options that control the details of the plots

The following list provides details about these options.

COVARIANCE COV

computes the principal components from the covariance matrix. If you omit the COV option, the correlation matrix is analyzed. The COV option causes variables that have large variances to be more strongly associated with components that have large eigenvalues, it and causes variables that have small variances to be more strongly associated with components that have small eigenvalues. You should not specify the COV option unless the units in which the variables are measured are comparable or the variables are standardized in some way.

DATA=SAS-data-set

specifies the SAS data set to be analyzed. The data set can be an ordinary SAS data set or a TYPE=ACE, TYPE=CORR, TYPE=COV, TYPE=FACTOR, TYPE=SSCP, TYPE=UCORR, or TYPE=UCOV data set (see Appendix A: Special SAS Data Sets). Also, the PRINCOMP procedure can read the _TYPE_='COVB' matrix from a TYPE=EST data set. If you omit the DATA= option, the procedure uses the most recently created SAS data set.

N=number

specifies the number of principal components to be computed. The default is the number of variables. The value of the N= option must be an integer greater than or equal to 0.

NOINT

omits the intercept from the model. In other words, the NOINT option requests that the covariance or correlation matrix not be corrected for the mean. When you specify the NOINT option, the covariance matrix and, hence, the standard deviations are not corrected for the mean.

If you use a TYPE=SSCP data set as input to the PRINCOMP procedure and list the variable Intercept in the VAR statement, the procedure acts as if you had also specified the NOINT option. If you use the NOINT option and also create an OUTSTAT= data set, the data set is TYPE=UCORR or TYPE=UCOV rather than TYPE=CORR or TYPE=COV.

NOPRINT

suppresses the display of all output. This option temporarily disables the Output Delivery System (ODS). For more information about ODS, see Chapter 20: Using the Output Delivery System.

OUT=SAS-data-set

creates an output SAS data set to contain all the original data in addition to the principal component scores.

If you want to create a SAS data set in a permanent library, you must specify a two-level name. For more information about permanent libraries and SAS data sets, see SAS Language Reference: Concepts. For information about OUT= data sets, see the section Output Data Sets.

OUTSTAT=SAS-data-set

creates an output SAS data set to contain means, standard deviations, number of observations, correlations or covariances, eigenvalues, and eigenvectors. If you specify the COV option, the data set is TYPE=COV or TYPE=UCOV, depending on the NOINT option, and it contains covariances; otherwise, the data set is TYPE=CORR or TYPE=UCORR, depending on the NOINT option, and it contains correlations. If you specify the PARTIAL statement, the OUTSTAT= data set also contains R squares.

If you want to create a SAS data set in a permanent library, you must specify a two-level name. For more information about permanent libraries and SAS data sets, see SAS Language Reference: Concepts. For more information about OUTSTAT= data sets, see the section Output Data Sets.

PLOTS <(global-plot-options)> <= plot-request <(options)>> PLOTS <(global-plot-options)> <= (plot-request <(options)> <... plot-request <(options)>>)>

controls the plots that are produced through ODS Graphics. When you specify only one plot request, you can omit the parentheses around the plot request. Here are some examples:

plots=none
plots=(scatter pattern)
plots(unpack)=scree
plots(ncomp=3 flip)=(pattern(circles=0.5 1.0) score)

ODS Graphics must be enabled before plots can be requested. For example:

ods graphics on;
proc princomp plots=all;
   var x1--x10;
run;
ods graphics off;

For more information about enabling and disabling ODS Graphics, see the section Enabling and Disabling ODS Graphics in Chapter 21: Statistical Graphics Using ODS.

If ODS Graphics is enabled but you do not specify the PLOTS= option, PROC PRINCOMP produces the scree plot by default.

You can specify the following global-plot-options:

FLIP: flips or interchanges the X-axis and Y-axis dimensions of the component score plots and the component pattern plots. For example, if you have three components, the default plots (y * x) are Component 2 * Component 1, Component 3 * Component 1, and Component 3 * Component 2. When you specify PLOTS(FLIP), the plots are Component 1 * Component 2, Component 1 * Component 3, and Component 2 * Component 3.
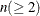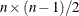NCOMP=n: specifies the number of components $n(\geq 2)$ to be plotted for the component pattern plots and the component score plots. If you specify the NCOMP= option again in an individual plot, such as PLOTS=SCORE(NCOMP= m), the value m determines the number of components to be plotted in the component score plots. Be aware that the number of plots ( $n \times (n-1) / 2$ ) that are produced grows quadratically when n increases. The default is 5 or the total number of components 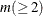$m(\geq 2)$ , whichever is smaller. If 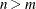$n>m$ , NCOMP=m is used.
ONLY: suppresses the default plots. Only plots that you specifically request are displayed.
UNPACKPANEL UNPACK: suppresses paneling in the scree plot. By default, multiple plots can appear in an output panel. Specify UNPACKPANEL to get each plot to appear in a separate panel. You can specify PLOTS(UNPACKPANEL) to unpack the default plots. You can also specify UNPACKPANEL as a suboption with the SCREE option (such as PLOTS=SCREE(UNPACKPANEL)).

You can specify the following plot-requests:

ALL

produces all appropriate plots. You can specify other options along with ALL; for example, to request all plots and unpack only the scree plot, specify PLOTS=(ALL SCREE(UNPACKPANEL)).

EIGEN | EIGENVALUE | SCREE < ( UNPACKPANEL ) >

produces the scree plot of eigenvalues and proportion variance explained. By default, both plots appear in the same panel. Specify PLOTS= SCREE(UNPACKPANEL) to get each plot to appear in a separate panel.

MATRIX

produces the matrix plot of principal component scores.

NONE

suppresses the display of all graphics output.

PATTERN < ( pattern-options ) >

produces the pairwise component pattern plots. Each variable is plotted as an observation whose coordinates are correlations between the variable and the two corresponding components in the plot. Use the NCOMP= option (for instance, PLOTS=PATTERN(NCOMP=3)) as described in the following list to control the number of plots to display.

You can specify the following pattern-options:

CIRCLES < = number-list >: plots the variance percentage circles. For each number c (0 < $c \le 1$ ) that is specified, a ( $c \times 100\%$ ) variance circle is displayed. For each number c ( $c > 1$ ) that is specified, a c% variance circle is displayed. You can specify either CIRCLES=0.05 1 or CIRCLES=5 100 to display 5% and 100% variance circles. PLOTS=PATTERN(CIRCLES) and PLOTS=PATTERN(VECTOR) both display a unit circle (100% variance). By default, no circle is displayed when you specify PLOTS=PATTERN.
FLIP: flips or interchanges the X-axis and Y-axis dimensions of the component pattern plots. Specify PLOTS=PATTERN(FLIP) to flip the X-axis and Y-axis dimensions.
NCOMP=n: specifies the number of components $n(\geq 2)$ to be plotted. The default is 5 or the total number of components $m(\geq 2)$ , whichever is smaller. If $n>m$ , NCOMP=m is used. Be aware that the number of plots ( $n \times (n-1) / 2$ ) that are produced grows quadratically when n increases.
VECTOR: plots the pattern in a vector form.

PATTERNPROFILE | PROFILE

produces the pattern profile plot. Each component has its own profile. The Y-axis value represents the correlation between the variable (corresponding to the X-axis value) and the profiled principal component.

SCORE < ( score-options ) >

produces the pairwise component score plots. Use the NCOMP= option (for example, PLOTS=SCORE(NCOMP=3)) as described in the following list to control the number of plots to display.

You can specify the following score-options.

ALPHA=number list

specifies a list of numbers for the prediction ellipses to be displayed in the score plots. Each value ( $\alpha$ ) in the list must be greater than 0. If $\alpha$ is greater than or equal to 1, it is interpreted as a percentage and divided by 100; ALPHA=0.05 and ALPHA=5 are equivalent.

ELLIPSE

requests prediction ellipses for the principal component scores of a new observation to be created in the principal component score plots. For information about the computation of a prediction ellipse, see the section "Confidence and Prediction Ellipses" in "The CORR Procedure" ( Base SAS Procedures Guide: Statistical Procedures).

FLIP

flips or interchanges the X-axis and Y-axis dimensions of the component score plots. Specify PLOTS=SCORE(FLIP) to flip the X-axis and Y-axis dimensions.

NCOMP=n

specifies the number of components 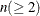$n(\geq 2)$ to be plotted. The default is 5 or the total number of components 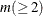$m(\geq 2)$ , whichever is smaller. If 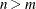$n>m$ , NCOMP=m is used. Be aware that the number of plots ( 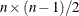$n \times (n-1) / 2$ ) that are produced grows quadratically when n increases.

PAINT <=position>

creates plots of component i versus component j, painted by component k. When you have at least three components, the PLOTS=SCORE option is specified, and the PAINT option is not specified, a painted score plot for component 3 versus component 2, painted by component 1, is produced. Use the PAINT option when you want to create painted score plots that involve other triples of components.

PLOTS=SCORE(PAINT), PLOTS=SCORE(PAINT=F), and PLOTS=SCORE(PAINT= FIRST) are all equivalent and create painted plots of 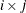$i \times j$ , painted by k for triples 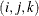$(i,j,k)$ , where $k < j < i$ .

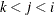PLOTS=SCORE(PAINT=L) and PLOTS=SCORE(PAINT=LAST) are equivalent and create painted plots of 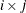$i \times j$ , painted by k for triples 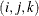$(i,j,k)$ , where $j < i < k$ .

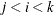PLOTS=SCORE(PAINT=M) and PLOTS=SCORE(PAINT=MIDDLE) are equivalent and create painted plots of 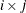$i \times j$ , painted by k for triples 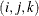$(i,j,k)$ , where $j < k < i$ .

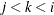PREFIX=name

specifies a prefix for naming the principal components. By default, the names are Prin1, Prin2, …, Prinn. If you specify PREFIX=Abc, the components are named Abc1, Abc2, Abc3, and so on. The number of characters in the prefix plus the number of digits required to designate the variables should not exceed the current name length that is defined by the VALIDVARNAME= system option.

PARPREFIX=name PPREFIX=name RPREFIX=name

specifies a prefix for naming the residual variables in the OUT= data set and the OUTSTAT= data set. By default, the prefix is R_. The number of characters in the prefix plus the maximum length of the variable names should not exceed the current name length that is defined by the VALIDVARNAME= system option.

SINGULAR=p SING=p

specifies the singularity criterion, where 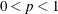$0<p<1$ . If a variable in a PARTIAL statement has an R square as large as 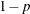$1-p$ when predicted from the variables listed before it in the statement, the variable is assigned a standardized coefficient of 0. By default, SINGULAR=1E–8.

STANDARD STD

standardizes the principal component scores in the OUT= data set to unit variance. If you omit the STANDARD option, the scores have variance equal to the corresponding eigenvalue. Note that the STANDARD option has no effect on the eigenvalues themselves.

VARDEF=DF | N | WDF | WEIGHT | WGT

specifies the divisor to be used in calculating variances and standard deviations. By default, VARDEF=DF. The following table displays the values and associated divisors:

Value	Divisor	Formula
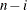
DF	Error degrees of freedom	$n-i$	(before partialing)
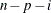
		$n-p-i$	(after partialing)
N	Number of observations	n
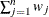
WEIGHT \| WGT	Sum of weights	$\sum _{j=1}^ n w_ j$
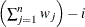
WDF	Sum of weights minus one	$\left( \sum _{j=1}^ n w_ j \right) - i$	(before partialing)
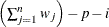
		$\left( \sum _{j=1}^ n w_ j \right) - p - i$	(after partialing)

In the formulas for VARDEF=DF and VARDEF=WDF, p is the number of degrees of freedom of the variables in the PARTIAL statement, and i is 0 if the NOINT option is specified and 1 otherwise.