The VARMAX Procedure

I(2) Model

Subsections:

Test for I(2)

The VARX( $p$ , $s$ ) model can be written in the error correction form:

$\begin{eqnarray*} \Delta \mb {y} _{t} = \balpha \bbeta ’ \mb {y} _{t-1} + \sum _{i=1}^{p-1} \Phi ^*_ i \Delta \mb {y} _{t-i} + A D_ t + \sum _{i=0}^{s}\Theta ^*_ i\mb {x} _{t-i} + \bepsilon _ t \end{eqnarray*}$

Let $\Phi ^* = I_ k - \sum _{i=1}^{p-1} \Phi ^*_ i$ .

If $\balpha$ and $\bbeta$ have full-rank $r$ , and $rank(\balpha ’_{\bot } \Phi ^* \bbeta _{\bot }) =k-r$ , then $\mb {y} _{t}$ is an $I(1)$ process.

If the condition $rank(\balpha ’_{\bot } \Phi ^* \bbeta _{\bot }) =k-r$ fails and $\balpha ’_{\bot } \Phi ^* \bbeta _{\bot }$ has reduced-rank $\balpha ’_{\bot } \Phi ^* \bbeta _{\bot }=\bxi \bm {\eta }’$ where $\bxi$ and $\bm {\eta }$ are $(k-r)\times s$ matrices with $s\leq k-r$ , then $\balpha _{\bot }$ and $\bbeta _{\bot }$ are defined as $k\times (k-r)$ matrices of full rank such that $\balpha ’\balpha _{\bot }=0$ and $\bbeta ’\bbeta _{\bot }=0$ .

If $\bxi$ and $\bm {\eta }$ have full-rank $s$ , then the process $\mb {y} _ t$ is $I(2)$ , which has the implication of $I(2)$ model for the moving-average representation.

$\begin{eqnarray*} \mb {y} _ t = B_0 + B_1 t + C_2\sum _{j=1}^ t\sum _{i=1}^ j\bepsilon _ i + C_1\sum _{i=1}^ t\bepsilon _ i + C_0(B)\bepsilon _ t \end{eqnarray*}$

The matrices $C_1$ , $C_2$ , and $C_0(B)$ are determined by the cointegration properties of the process, and $B_0$ and $B_1$ are determined by the initial values. For details, see Johansen (1995b).

The implication of the $I(2)$ model for the autoregressive representation is given by

$\begin{eqnarray*} \Delta ^2 \mb {y} _{t} = \Pi \mb {y} _{t-1} -\Phi ^* \Delta \mb {y} _{t-1} + \sum _{i=1}^{p-2} \Psi _ i \Delta ^2 \mb {y} _{t-i} + A D_ t + \sum _{i=0}^{s}\Theta ^*_ i\mb {x} _{t-i} +\bepsilon _ t \end{eqnarray*}$

where $\Psi _ i = -\sum _{j=i+1}^{p-1} \Phi ^*_ i$ and $\Phi ^* = I_ k - \sum _{i=1}^{p-1} \Phi ^*_ i$ .

Test for I(2)

The $I(2)$ cointegrated model is given by the following parameter restrictions:

$\begin{eqnarray*} H_{r,s}\colon \Pi =\balpha \bbeta ’\; \mbox{and}\; \balpha _{\bot }’\Phi ^* \bbeta _{\bot } = \bxi \bm {\eta }’ \end{eqnarray*}$

where $\bxi$ and $\bm {\eta }$ are $(k-r)\times s$ matrices with $0\leq s \leq k-r$ . Let $H_ r^0$ represent the $I(1)$ model where $\balpha$ and $\bbeta$ have full-rank $r$ , let $H_{r,s}^0$ represent the $I(2)$ model where $\bxi$ and $\bm {\eta }$ have full-rank $s$ , and let $H_{r,s}$ represent the $I(2)$ model where $\bxi$ and $\bm {\eta }$ have rank $\leq s$ . The following table shows the relation between the $I(1)$ models and the $I(2)$ models.

Table 35.6: Relation between the $I(1)$ and $I(2)$ Models

					$I(2)$					$I(1)$
$r \backslash k-r-s$	k		k-1		$\cdots$		$1$
0	$H_{00}$	$\subset$	$H_{01}$	$\subset$	$\cdots$	$\subset$	$H_{0,k-1}$	$\subset$	$H_{0k}$	$=$	$H_{0}^0$
1			$H_{10}$	$\subset$	$\cdots$	$\subset$	$H_{1,k-2}$	$\subset$	$H_{1,k-1}$	$=$	$H_{1}^0$
$\vdots$							$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$
$k-1$							$H_{k-1,0}$	$\subset$	$H_{k-1,1}$	$=$	$H_{k-1}^0$

Johansen (1995b) proposed the two-step procedure to analyze the $I(2)$ model. In the first step, the values of $(r, \balpha , \bbeta )$ are estimated using the reduced rank regression analysis, performing the regression analysis $\Delta ^2\mb {y} _{t}$ , $\Delta \mb {y} _{t-1}$ , and $\mb {y} _{t-1}$ on $\Delta ^2\mb {y} _{t-1},\ldots ,\Delta ^2\mb {y} _{t-p+2},$ and $D_ t$ . This gives residuals $R_{0t}$ , $R_{1t}$ , and $R_{2t}$ , and residual product moment matrices

$M_{ij} = \frac{1}{T} \sum _{t=1}^ TR_{it}R_{jt}’ ~ ~ \mr {for~ ~ } i,j=0,1,2$

Perform the reduced rank regression analysis $\Delta ^2\mb {y} _{t}$ on $\mb {y} _{t-1}$ corrected for $\Delta \mb {y} _{t-1}$ , $\Delta ^2\mb {y} _{t-1},\ldots ,\Delta ^2\mb {y} _{t-p+2},$ and $D_ t$ , and solve the eigenvalue problem of the equation

$|\lambda M_{22\mb {.} 1} - M_{20\mb {.} 1}M_{00\mb {.} 1}^{-1}M_{02\mb {.} 1}| = 0$

where $M_{ij\mb {.} 1} = M_{ij} - M_{i1}M_{11}^{-1}M_{1j}$ for $i,j=0,2$ .

In the second step, if $(r, \balpha , \bbeta )$ are known, the values of $(s, \bxi , \bm {\eta })$ are determined using the reduced rank regression analysis, regressing $\hat{\balpha }_{\bot }’\Delta ^2\mb {y} _{t}$ on $\hat{\bbeta }_{\bot }’\Delta \mb {y} _{t-1}$ corrected for $\Delta ^2\mb {y} _{t-1},\ldots ,\Delta ^2\mb {y} _{t-p+2},D_ t$ , and $\hat{\bbeta }’\Delta \mb {y} _{t-1}$ .

The reduced rank regression analysis reduces to the solution of an eigenvalue problem for the equation

$\begin{eqnarray*} |\rho M_{\bbeta _{\bot }\bbeta _{\bot }\mb {.} \bbeta } - M_{\bbeta _{\bot }\balpha _{\bot }\mb {.} \bbeta } M_{\balpha _{\bot }\balpha _{\bot }\mb {.} \bbeta }^{-1} M_{\balpha _{\bot }\bbeta _{\bot }\mb {.} \bbeta }| = 0 \end{eqnarray*}$

where

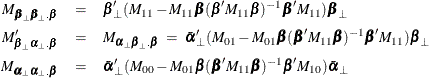
$\begin{eqnarray*} M_{\bbeta _{\bot }\bbeta _{\bot }\mb {.} \bbeta } & = & \bbeta _{\bot }’(M_{11} - M_{11}\bbeta (\bbeta ’M_{11}\bbeta )^{-1}\bbeta ’M_{11})\bbeta _{\bot } \\ M_{\bbeta _{\bot }\balpha _{\bot }\mb {.} \bbeta }’ & = & M_{\balpha _{\bot }\bbeta _{\bot }\mb {.} \bbeta } ~ =~ \bar{\balpha }_{\bot }’(M_{01} - M_{01}\bbeta (\bbeta ’M_{11}\bbeta )^{-1}\bbeta ’M_{11})\bbeta _{\bot } \\ M_{\balpha _{\bot }\balpha _{\bot }\mb {.} \bbeta } & = & \bar{\balpha }_{\bot }’(M_{00} - M_{01}\bbeta (\bbeta ’M_{11}\bbeta )^{-1}\bbeta ’M_{10})\bar{\balpha }_{\bot } \end{eqnarray*}$

where $\bar{\balpha }=\balpha (\balpha ’\balpha )^{-1}$ .

The solution gives eigenvalues $1>\rho _1>\cdots >\rho _ s>0$ and eigenvectors $(v_1,\ldots , v_ s)$ . Then, the ML estimators are

$\begin{eqnarray*} \hat{\bm {\eta }} & = & (v_1,\ldots , v_ s) \\ \hat{\bxi } & = & M_{\balpha _{\bot }\bbeta _{\bot }\mb {.} \bbeta }\hat{\eta } \end{eqnarray*}$

The likelihood ratio test for the reduced rank model $H_{r,s}$ with rank $\leq s$ in the model $H_{r,k-r} = H_ r^0$ is given by

$\begin{eqnarray*} Q_{r,s} = -T\sum _{i=s+1}^{k-r}\log (1-\rho _ i), ~ ~ s=0,\ldots ,k-r-1 \end{eqnarray*}$

The following statements compute the rank test to test for cointegrated order 2:

proc varmax data=simul2;
   model y1 y2 / p=2 cointtest=(johansen=(iorder=2));
run;

The last two columns in Figure 35.60 explain the cointegration rank test with integrated order 1. The results indicate that there is the cointegrated relationship with the cointegration rank 1 with respect to the 0.05 significance level because the test statistic of 0.5552 is smaller than the critical value of 3.84. Now, look at the row associated with $r=1$ . Compare the test statistic value, 211.84512, to the critical value, 3.84, for the cointegrated order 2. There is no evidence that the series are integrated order 2 at the 0.05 significance level.

Figure 35.60: Cointegrated I(2) Test (IORDER= Option)

The VARMAX Procedure

Cointegration Rank Test for I(2)
r\k-r-s	2	1	Trace of I(1)	5% CV of I(1)
0	720.40735	308.69199	61.7522	15.34
1		211.84512	0.5552	3.84
5% CV I(2)	15.34000	3.84000