The VARMAX Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues
Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues -
Examples

- References
RESTRICT restriction, …, restriction ;
The RESTRICT statement places linear restrictions on the parameters and provides constrained estimation. Only one RESTRICT statement is allowed. If you specify more than one restriction in a RESTRICT statement, separate them with commas. Both equality and inequality constraints are allowed in the RESTRICT statement, although in general, the equality constraints are specified in the RESTRICT statement, and the inequality constraints are specified in the BOUND statement. If the least squares method is used, the inequality constraints are not applicable.
To use the RESTRICT statement, you need to know the form of the model. If you do not specify the P=, Q=, or XLAG= option or the GARCH statement, then the RESTRICT statement is not applicable. Nonlinear restrictions on parameters are not supported.
You compute restricted parameter estimates by introducing a Lagrangian parameter for each restriction (Pringle and Rayner, 1971). The Lagrangian parameter measures the sensitivity of the sum of squared errors to the restriction. The estimates of these Lagrangian parameters and their significance are printed in the Restrict ODS table.
The RESTRICT statement operates on matrices. That is, you can specify the parameter matrices or constant matrices through
the RESTRICT statement’s built-in operators and functions. You can add elements of the matrices A and B with the expression A+B, and you can perform matrix multiplication with the expression A*B and elementwise multiplication with the expression A#B. You can get the diagonal elements of the matrix A through the function DIAG(A), and you can get the ![]() identity matrix through the function
identity matrix through the function I(n).
Each restriction is written as a matrix expression composed of constants, operators, and functions.
Constants are either scalar constants, such as ![]() ,
, ![]() ,
, ![]() , or matrix constants enclosed in braces, such as
, or matrix constants enclosed in braces, such as ![]() matrix
matrix {1 2, 3 4}, ![]() matrix (or called row vector)
matrix (or called row vector) {-0.2 5.3 12}, and so on. Constants also include the dependent variable names and exogenous variable names that represent their index values
and are mostly used in the subscripts or function arguments. For example, in the following statement, according to the order
of the dependent and exogenous variables in the MODEL statement, GDP is equal to 1, CPI to 2, M2 to 3, FFR to 1, and CP to
2. Hence, the function call AR(2, GDP, {CPI M2}) is equivalent to AR(2,1,{2 3}), and XL(0, CPI, {FFR CP}) is equivalent to XL(0,2,{1 2}). The use of AR and XL functions to access parameters is discussed in the section Functions.
proc varmax data=macrodata;
model GDP CPI M2 = FFR CP / p=12 xlag=12;
restrict AR(2, GDP, {CPI M2}) = 0,
XL(0, CPI, {FFR CP}) = 0;
run;
The matrix constant cannot be the first item in the RESTRICT statement. For example, you cannot specify the following statement:
restrict {-0.1 -0.2, -0.3 -0.4} <= AR <= {0.1 0.2, 0.3 0.4};
You can put the first matrix constant in parentheses and specify the preceding example in the following way:
restrict ({-0.1 -0.2, -0.3 -0.4}) <= AR <= {0.1 0.2, 0.3 0.4};
Operators define the operations on operands. Table 35.2 lists all built-in operators supported by the RESTRICT statement.
Table 35.2: Operators
|
Operator |
Name |
Description |
|---|---|---|
|
+ |
Addition |
Adds corresponding matrix elements |
|
= |
Comparison, equal |
Compares matrix elements |
|
< |
Comparison, less than |
Compares matrix elements |
|
<= |
Comparison, not greater than |
Compares matrix elements |
|
> |
Comparison, greater than |
Compares matrix elements |
|
>= |
Comparison, not less than |
Compares matrix elements |
|
|| |
Concatenation, horizontal |
Concatenates matrices horizontally |
|
// |
Concatenation, vertical |
Concatenates matrices vertically |
|
@ |
Direct product |
Takes the direct product of two matrices |
|
: |
Index creation |
Creates an index vector |
|
# |
Multiplication, elementwise |
Performs elementwise multiplication |
|
Multiplication, matrix |
Performs matrix multiplication |
|
|
|
Sign reverse |
Reverses the signs of elements |
|
|
Subscripts |
Selects submatrices |
|
|
Subtraction |
Subtracts corresponding matrix elements |
|
` |
Transpose |
Transposes a matrix |
For more information about each operator, see the section Details of Operators.
Table 35.3 shows the precedence of matrix operators in the RESTRICT statement.
Table 35.3: Operator Precedence
|
Priority Group |
Operators |
||||||
|---|---|---|---|---|---|---|---|
|
I (highest) |
|
|
|||||
|
II |
|
||||||
|
III |
* |
# |
@ |
||||
|
IV |
|
+ |
|||||
|
V |
|| |
// |
: |
||||
|
VI (lowest) |
= |
< |
<= |
> |
>= |
||
Each restriction can be a compound expression that involves several matrix operators and operands. The rules for evaluating compound expressions are as follows:
-
Evaluation follows the order of operator precedence, as described in Table 35.3. Group I has the highest priority; that is, Group I operators are evaluated first. Group II operators are evaluated after Group I operators, and so on. For example,
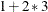 returns
returns 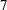 .
.
-
If neighboring operators in an expression have equal precedence, the expression is evaluated from left to right, except for the Group I operators. For example,
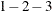 returns
returns 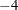 .
.
-
All expressions in parentheses are evaluated first, following the two preceding rules. For example,
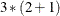 returns
returns 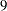 .
.
Functions are mainly divided into two categories: one type of function refers to parameters to be estimated, such as AR(L,I,J) and CCC(I,J); the other type does not, such as I(n) and DIAG(A).
Functions that refer to the parameters are listed in Table 35.4. The arguments for functions can be matrices. The simplest case, scalar arguments, is discussed first. For convenience, the
scalar indices i and j refer to the position of the element in the coefficient matrix, and scalar l refers to the lag value.
Table 35.4: Functions Referring to Parameters
|
Function |
Description |
|---|---|
|
|
ARCH parameter of the lag |
|
|
Autoregressive parameter of the lag |
|
|
Constant conditional correlation parameter between |
|
|
Intercept parameter of the |
|
|
Covariance of innovations parameter between |
|
|
Parameter |
|
|
Parameter |
|
|
Unconditional correlation parameter between |
|
|
Exponential ARCH parameter of the lag |
|
|
GARCH parameter of the lag |
|
|
Constant parameter of the covariance matrix, |
|
|
Power parameter for the |
|
|
Linear trend parameter of the |
|
|
Moving-average parameter of the lag |
|
|
Power ARCH parameter of the lag |
|
|
Quadratic ARCH center parameter of the lag |
|
|
Quadratic trend parameter of the |
|
|
Same as |
|
|
|
|
|
Threshold ARCH parameter of the lag |
|
|
Exogenous parameter of the lag |
The functions that refer to parameters, as shown in Table 35.4, accept vector arguments and return the matrix constructed by the corresponding parameters. According to the number of arguments, the following list shows what matrix a function returns when the arguments are vectors:
-
A function
FUNC0, namelyDCCAandDCCB, with zero arguments, always returns the corresponding scalar parameter. -
A function
FUNC1, namelyCONST,LAMBDA,LTREND, andQTREND, with one vector argument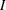 , where
, where 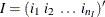 , returns a vector
, returns a vector 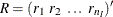 , where
, where 
FUNC1(
), .
.
-
A function
FUNC2, namelyCCC,COV,DCCS,GCHC,SD, andSDUMMY, with two vector arguments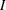 and
and 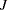 , where
, where 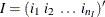 and
and 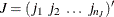 , returns a matrix
, returns a matrix
![\[ R= \left( \begin{array}{cccc} r_{1,1} & r_{1,2} & \cdots & r_{1,n_ J} \\ r_{2,1} & r_{2,2} & \cdots & r_{2,n_ J} \\ \cdots & & & \\ r_{n_ I,1} & r_{n_ I,2} & \cdots & r_{n_ I,n_ J} \\ \end{array} \right) \]](images/etsug_varmax0240.png)
where
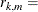
FUNC2(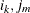
),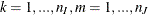 .
.
-
A function
FUNC3, namelyACH,AR,EACH,GCH,MA,PACH,QACH,TACH, andXL, with three vector arguments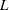 ,
, 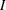 , and
, and 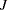 , where
, where 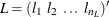 ,
, 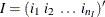 , and
, and 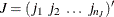 , returns a matrix
, returns a matrix
![\[ R= \left( \begin{array}{cccc} r_{1,1} & r_{1,2} & \cdots & r_{1,n_ L n_ J} \\ r_{2,1} & r_{2,2} & \cdots & r_{2,n_ L n_ J} \\ \cdots & & & \\ r_{n_ I,1} & r_{n_ I,2} & \cdots & r_{n_ I,n_ L n_ J} \\ \end{array} \right) \]](images/etsug_varmax0246.png)
where
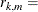
FUNC3(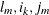
),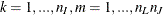 , and
, and 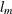 and
and 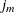 are the quotient and remainder of
are the quotient and remainder of 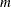 divided by
divided by 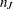 , respectively.
, respectively.
The functions that refer to parameters can accept empty arguments or omit any number of last arguments. The empty or omitted
arguments are replaced with all possible values for those arguments. For example, in a bivariate (![]() =2) VARX(1,1) model with three exogenous variables,
=2) VARX(1,1) model with three exogenous variables,
model y1 y2 = x1 x2 x3 / p=1 xlag=3;
in order to restrict the third exogenous variable from having an effect on the first dependent variable, and to restrict the first exogenous variable from having an effect on the second dependent variable, you can use the following statement:
restrict XL({0 1 2 3}, 1, 3) = 0,
XL({0 1 2 3}, 2, 1) = 0;
Taking advantage of empty arguments, you can specify the preceding example as follows:
restrict XL( , 1, 3) = 0,
XL( , 2, 1) = 0;
To get all coefficients of the first lag exogenous variables on dependent variables, you can use XL(1, {1 2}, {1 2 3}) or XL(1, , ) or XL(1). To get all coefficients of exogenous variables on dependent variables, you can use XL({0 1 2 3}, {1 2}, {1 2 3}), or XL( , , ) or XL() or even just XL.
Another type of function does not refer to parameters but generates useful matrices. Table 35.5 lists all built-in functions supported by the RESTRICT statement.
Table 35.5: Functions Not Referring to Parameters
|
Function |
Description |
|---|---|
|
|
Creates a diagonal matrix from a vector or extracts the diagonal elements of a matrix |
|
|
Creates an |
|
|
Creates an |
|
|
Creates a |
For more information about each function in Table 35.5, see the section Details of Functions.
The following examples show how to use the RESTRICT statement.
This example shows a bivariate (![]() =2) VAR(2) model:
=2) VAR(2) model:
proc varmax data=one; model y1 y2 / p=2; restrict AR(1,1,2)=0, AR(2,1,2)=0.3; run;
The AR(1,1,2) and AR(2,1,2) parameters are fixed as AR(1,1,2)=0 and AR(2,1,2)=0.3, respectively, and other parameters are to be estimated.
The following example shows a bivariate (![]() =2) VAR(1) model, estimated using the ML method:
=2) VAR(1) model, estimated using the ML method:
proc varmax data=two; model y1 y2 = / p=1 method=ml; restrict cov(1,1)=cov(2,2), cov(1,2)=0; run;
The COV(1,1) and COV(2,2) parameters are equal, and the correlation between the two series is fixed at 0. You can also express the preceding restrictions
in matrix expressions as follows; this approach is very convenient when the number of dependent variables is large:
proc varmax data=two; model y1 y2 = / p=1 method=ml; restrict cov = cov(1,1)*I(2); run;
When restricting a linear combination of parameters to be 0, you can omit the equal sign. For example, the following two RESTRICT statements are equivalent:
restrict AR(1)[1,1)-AR(1)[2,2], 2*MA(1)[1,2]-MA(1)[2,1];
restrict AR(1)[1,1]-AR(1)[2,2] = 0, 2*MA(1)[1,2]-MA(1)[2,1] = 0;
The following RESTRICT statement constrains four parameter estimates to be equal:
restrict AR(1)[1,1] = AR(1)[1,2],
AR(1)[1,2] = AR(1)[2,1],
AR(1)[2,1] = AR(1)[2,2];
This restriction can be abbreviated as follows:
restrict AR(1)[1,1] = AR(1)[1,2] = AR(1)[2,1] = AR(1)[2,2];
Or, in matrix expressions,
restrict AR(1,1:2,1:2) = J(2,2,AR(1,1,1));
The VARMA representation ![]() , where
, where ![]() and
and ![]() , is said to be in final equation form if
, is said to be in final equation form if ![]() , where
, where ![]() is a scalar operator with
is a scalar operator with ![]() . If
. If ![]() and
and ![]() are large, it would be difficult and inconvenient to restrict AR parameters element by element in standard form to estimate
the VARMA model in final equation form. However, when you use matrix expressions, the restrictions become very simple, as
shown in the following statement for a trivariate (
are large, it would be difficult and inconvenient to restrict AR parameters element by element in standard form to estimate
the VARMA model in final equation form. However, when you use matrix expressions, the restrictions become very simple, as
shown in the following statement for a trivariate (![]() ) VARMA(
) VARMA(![]() ,
, ![]() ) model, where
) model, where ![]() might be any positive integer:
might be any positive integer:
restrict AR = AR(,1,1) @ I(3);
This section describes all operators that are available in the RESTRICT statement. Each subsection shows how the operator is used, followed by a description of the operator.
matrix1 + matrix2
matrix + scalar
matrix + vector
The addition operator (+) computes a new matrix whose elements are the sums of the corresponding elements of matrix1 and matrix2. If matrix1 and matrix2 are both ![]() matrices, then the addition operator adds the element in the
matrices, then the addition operator adds the element in the ![]() th row and
th row and ![]() th column of the first matrix to the element in the
th column of the first matrix to the element in the ![]() th row and
th row and ![]() th column of the second matrix, for
th column of the second matrix, for ![]() . For example,
. For example, {1 2 3, 4 5 6} + {7 8 9, 10 11 12} results in {8 10 12, 14 16 18}.
You can also use the addition operator as follows to conveniently add a value to each element of a matrix, to each column of a matrix, or to each row of a matrix:
-
When you use the
matrix+scalarform, the scalar value is added to each element of the matrix. -
When you use the
matrix+vectorform, the vector is added to each row or column of the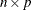 matrix.
matrix.
-
If you add an
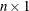 column vector, each row of the vector is added to each row of the matrix.
column vector, each row of the vector is added to each row of the matrix.
-
If you add a
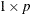 row vector, each column of the vector is added to each column of the matrix.
row vector, each column of the vector is added to each column of the matrix.
-
For example, you can obtain {2 3 4, 5 6 7} from {1 2 3, 4 5 6} + 1 or {1 2 3, 4 5 6} + {1 1 1} or {1 2 3, 4 5 6} + {1, 1}.
matrix1 = matrix2
matrix1 < matrix2
matrix1 <= matrix2
matrix1 > matrix2
matrix1 >= matrix2
The comparison operators (=, <, <=, >, >=) compare two matrices element by element and return a list of equivalent restrictions on only scalar constants and parameters.
For example, the RESTRICT statement with matrix expressions
restrict AR(1,{1,2},{1,2}) = MA(2,{3,4},{3,4});
is transformed into the following equivalent RESTRICT statement with scalar parameters:
restrict AR(1,1,1) = MA(2,3,3),
AR(1,1,2) = MA(2,3,4),
AR(1,2,1) = MA(2,4,3),
AR(1,2,2) = MA(2,4,4);
You can also use the comparison operators to conveniently compare all elements of a matrix with a scalar:
-
If either argument is a scalar, then the VARMAX procedure performs an elementwise comparison between each element of the matrix and the scalar.
You can also compare an ![]() matrix with a row or column vector:
matrix with a row or column vector:
-
If the comparison is with an
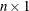 column vector, the VARMAX procedure compares each row of the vector to each row of the matrix.
column vector, the VARMAX procedure compares each row of the vector to each row of the matrix.
-
If the comparison is with a
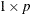 row vector, the VARMAX procedure compares each column of the vector to each column of the matrix.
row vector, the VARMAX procedure compares each column of the vector to each column of the matrix.
For example, the following statements are equivalent:
restrict AR(1,1:2,1:3) >= 0.2;
restrict AR(1,1:2,1:3) >= {0.2, 0.2};
restrict AR(1,1:2,1:3) >= {0.2 0.2 0.2};
matrix1
![]() matrix2
matrix2
The horizontal concatenation operator (||) produces a new matrix by horizontally joining matrix1 and matrix2. The matrices must have the same number of rows, which is also the number of rows in the new matrix. The number of columns
in the new matrix is the number of columns in matrix1 plus the number of columns in matrix2.
For example, {1 1 1, 7 7 7} || {0 0 0, 8 8 8} returns {1 1 1 0 0 0, 7 7 7 8 8 8}.
matrix1 // matrix2
The vertical concatenation operator (//) produces a new matrix by vertically joining matrix1 and matrix2. The matrices must have the same number of columns, which is also the number of columns in the new matrix. The number of
rows in the new matrix is the number of rows in matrix1 plus the number of rows in matrix2.
For example, {1 1 1} // {0 0 0, 8 8 8} returns {1 1 1, 0 0 0, 8 8 8}.
matrix1 @ matrix2
The direct product operator (@) computes a new matrix that is the direct product (also called the Kronecker product) of matrix1 and matrix2. For matrices ![]() and
and ![]() , the direct product is denoted by
, the direct product is denoted by ![]() . The number of rows in the new matrix equals the product of the number of rows in
. The number of rows in the new matrix equals the product of the number of rows in matrix1 and the number of rows in matrix2; the number of columns in the new matrix equals the product of the number of columns in matrix1 and the number of columns in matrix2.
Specifically, if ![]() is an
is an ![]() matrix and
matrix and ![]() is a
is a ![]() matrix, then the Kronecker product
matrix, then the Kronecker product ![]() is the following
is the following ![]() block matrix:
block matrix:
![\[ \mb {A}\otimes \mb {B}= \left[ \begin{matrix} A_{11} B & \cdots & A_{1p}B \cr \vdots & \ddots & \vdots \cr A_{n1} B & \cdots & A_{np} B \end{matrix} \right] \]](images/etsug_varmax0271.png)
For example, {1 2, 3 4} @ {0 2} returns {0 2 0 4, 0 6 0 8}, and {0 2} @ {1 2, 3 4} returns {0 0 2 4, 0 0 6 8}. Note that the direct product of two matrices is not commutative.
value1 : value2
The index creation operator (:) creates a column vector whose first element is value1, whose second element is value1+1, and so on, until the last element, which is less than or equal to value2.
For example, 3 : 6 returns {3 4 5 6}.
If value1 is greater than value2, a reverse-order index is created. For example, 6 : 3 returns {6 5 4 3}.
Neither value1 nor value2 is required to be an integer.
matrix1 # matrix2
matrix # scalar
matrix # vector
The elementwise multiplication operator (#) computes a new matrix whose elements are the products of the corresponding elements
of matrix1 and matrix2.
For example, {1 2, 3 4} # {4 8, 0 5} returns {4 16, 0 20}.
In addition to multiplying matrices that have the same dimensions, you can use the elementwise multiplication operator to multiply a matrix and a scalar:
-
When either argument is a scalar, each element in
matrixis multiplied by the scalar value.
When you use the matrix # vector form, each row or column of the ![]() matrix is multiplied by a corresponding element of the vector:
matrix is multiplied by a corresponding element of the vector:
-
If you multiply by an
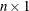 column vector, each row of the matrix is multiplied by the corresponding row of the vector.
column vector, each row of the matrix is multiplied by the corresponding row of the vector.
-
If you multiply by a
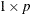 row vector, each column of the matrix is multiplied by the corresponding column of the vector.
row vector, each column of the matrix is multiplied by the corresponding column of the vector.
For example, a ![]() matrix can be multiplied on either side by a
matrix can be multiplied on either side by a ![]() ,
, ![]() ,
, ![]() , or
, or ![]() scalar.
scalar.
The product of elementwise multiplication is also known as the Schur or Hadamard product. Elementwise multiplication (which uses the # operator) should not be confused with matrix multiplication (which uses the * operator).
matrix1 * matrix2
The matrix multiplication operator (*) computes a new matrix by performing matrix multiplication. The first matrix must have
the same number of columns as the second matrix has rows. The new matrix has the same number of rows as the first matrix and
the same number of columns as the second matrix. That is, if ![]() is an
is an ![]() matrix and
matrix and ![]() is a
is a ![]() matrix, then the product
matrix, then the product ![]() is an
is an ![]() matrix. The
matrix. The ![]() th element of the product is the sum
th element of the product is the sum ![]() .
.
For example, {1 2, 3 4} * {1, 2} returns {5, 11}.
- matrix
The sign reversal operator (![]() ) computes a new matrix whose elements are formed by reversing the sign of each element in
) computes a new matrix whose elements are formed by reversing the sign of each element in matrix. The sign reversal operator is also called the unary minus operator.
For example, -{-1 7 6, 2 0 -8} returns {1 -7 -6, -2 0 8}.
matrix[rows, columns]
matrix[elements]
Subscripts are used with matrices to select submatrices, where rows, columns, and elements are expressions that evaluate to scalars or vectors. If these expressions are numeric, they must contain valid subscript
values of rows and columns, or the indices, in the argument matrix.
For example, {1 2 3, 4 5 6, 7 8 9}[2,3] returns 6, {1 2 3, 4 5 6, 7 8 9}[2,1:3] returns {4 5 6}, and {1 2 3, 4 5 6, 7 8 9}[,3] returns {3, 6, 9}. Because the VARMAX procedure stores matrices in row-major order, {11 22 33, 44 55 66, 77 88 99}[{3 5 9}] returns {33, 55, 99}.
matrix1 - matrix2
matrix - scalar
matrix - vector
The subtraction operator (![]() ) computes a new matrix whose elements are formed by subtracting the corresponding elements of
) computes a new matrix whose elements are formed by subtracting the corresponding elements of matrix2 from those of matrix1.
In addition to subtracting conformable matrices, you can also use the subtraction operator to subtract a scalar from a matrix or subtract a vector from a matrix:
-
When either argument is a scalar, the VARMAX procedure performs the subtraction between the scalar and each element of the matrix argument. For example, when you use the
matrix - scalarform, the scalar value is subtracted from each element of the matrix. -
When you use the
matrix - vectorform, the vector is subtracted from each row or column of the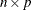 matrix.
matrix.
-
If you subtract an
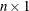 column vector, each row of the vector is subtracted from each row of the matrix.
column vector, each row of the vector is subtracted from each row of the matrix.
-
If you subtract a
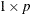 row vector, each column of the vector is subtracted from each column of the matrix.
row vector, each column of the vector is subtracted from each column of the matrix.
-
For example, {1 2 3, 4 5 6} - {1 1 1, 1 1 1} returns {0 1 2, 3 4 5}. The same results can be obtained by {1 2 3, 4 5 6} - 1 or {1 2 3, 4 5 6} - {1 1 1} or {1 2 3, 4 5 6} - {1, 1}.
matrix`
The transpose operator, denoted by the backquote character (`), exchanges the rows and columns of matrix, producing the transpose of matrix. If ![]() is the value in the
is the value in the ![]() th row and
th row and ![]() th column of
th column of matrix, then the transpose of matrix contains ![]() in the
in the ![]() th row and
th row and ![]() th column. If
th column. If matrix contains ![]() rows and
rows and ![]() columns, the transpose has
columns, the transpose has ![]() rows and
rows and ![]() columns.
columns.
For example, {1 2, 3 4, 5 6}` returns {1 3 5, 2 4 6}.
DIAG(matrix)
The DIAG function creates a diagonal matrix from a vector or extracts the diagonal elements of a matrix. The matrix argument can be either a square matrix or a vector.
If matrix is a vector, the DIAG function creates a matrix whose diagonal elements are the values in the vector. All off-diagonal elements are zeros.
If matrix is a square matrix, the DIAG function creates a vector from the diagonal elements of the matrix.
For example, DIAG({1 2 3, 4 5 6, 7 8 9}) returns {1, 5, 9}. Also, DIAG({1 5 9}) or DIAG({1, 5, 9}) or DIAG(DIAG({1 2 3, 4 5 6, 7 8 9})) returns {1 0 0, 0 5 0, 0 0 9}.
I(dim)
The I function creates an identity matrix that contains dim rows and columns. The diagonal elements of an identity matrix are ones; all other elements are zeros. The value of dim must be an integer greater than or equal to 1. Noninteger operands are rounded to the nearest integer.
For example, I(3) returns {1 0 0, 0 1 0, 0 0 1}.
J(nrow, ncol, value)
The J function creates a matrix that contains nrow rows and ncol columns, in which all elements are equal to value.
The arguments nrow and ncol are both integers; value can be any expression that returns a linear combination of scalar constants and parameters.
For example, J(2, 3, 1) returns {1 1 1, 1 1 1}. J(2, 3, 5+2*AR(1,1,1)) returns the same result as J(2, 3, 1) * (5+2*AR(1,1,1)).
SHAPE(matrix, nrow, ncol)
The SHAPE function creates a new matrix from data in matrix. The values nrow and ncol specify the number of rows and columns, respectively, in the new matrix. The SHAPE function produces the result matrix by traversing the argument matrix in row-major order until it reaches the specified number
of elements. If necessary, the SHAPE function reuses elements.
For example, SHAPE({1 2 3, 4 5 6}, 3, 2) returns {1 2, 3 4, 5 6}; SHAPE({1 2 3, 4 5 6}, 5, 2) returns {1 2, 3 4, 5 6, 1 2, 3 4}; and SHAPE({1 2 3, 4 5 6}, 1, 4) returns {1 2 3 4}.