The VARMAX Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues
Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues -
Examples

- References
This section briefly introduces the concepts of cointegration (Johansen, 1995a).
- Definition 1.
-
(Engle and Granger, 1987): If a series
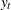 with no deterministic components can be represented by a stationary and invertible ARMA process after differencing d times, the series is integrated of order d, that is,
with no deterministic components can be represented by a stationary and invertible ARMA process after differencing d times, the series is integrated of order d, that is, 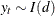 .
.
- Definition 2.
-
(Engle and Granger, 1987): If all elements of the vector
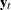 are
are 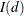 and there exists a cointegrating vector
and there exists a cointegrating vector 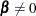 such that
such that 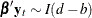 for any
for any 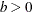 , the vector process is said to be cointegrated
, the vector process is said to be cointegrated 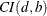 .
.
A simple example of a cointegrated process is the following bivariate system:
with ![]() and
and ![]() being uncorrelated white noise processes. In the second equation,
being uncorrelated white noise processes. In the second equation, ![]() is a random walk,
is a random walk, ![]() ,
, ![]() . Differencing the first equation results in
. Differencing the first equation results in
Thus, both ![]() and
and ![]() are
are ![]() processes, but the linear combination
processes, but the linear combination ![]() is stationary. Hence
is stationary. Hence ![]() is cointegrated with a cointegrating vector
is cointegrated with a cointegrating vector ![]() .
.
In general, if the vector process ![]() has k components, then there can be more than one cointegrating vector
has k components, then there can be more than one cointegrating vector ![]() . It is assumed that there are r linearly independent cointegrating vectors with
. It is assumed that there are r linearly independent cointegrating vectors with ![]() , which make the
, which make the ![]() matrix
matrix ![]() . The rank of matrix
. The rank of matrix ![]() is r, which is called the cointegration rank of
is r, which is called the cointegration rank of ![]() .
.
This section briefly discusses the implication of cointegration for the moving-average representation. Let ![]() be cointegrated
be cointegrated ![]() , then
, then ![]() has the Wold representation:
has the Wold representation:
where ![]() is
is ![]() ,
, ![]() with
with ![]() , and
, and ![]() .
.
Assume that ![]() if
if ![]() and
and ![]() is a nonrandom initial value. Then the difference equation implies that
is a nonrandom initial value. Then the difference equation implies that
where ![]() and
and ![]() is absolutely summable.
is absolutely summable.
Assume that the rank of ![]() is
is ![]() . When the process
. When the process ![]() is cointegrated, there is a cointegrating
is cointegrated, there is a cointegrating ![]() matrix
matrix ![]() such that
such that ![]() is stationary.
is stationary.
Premultiplying ![]() by
by ![]() results in
results in
because ![]() and
and ![]() .
.
Stock and Watson (1988) showed that the cointegrated process ![]() has a common trends representation derived from the moving-average representation. Since the rank of
has a common trends representation derived from the moving-average representation. Since the rank of ![]() is
is ![]() , there is a
, there is a ![]() matrix
matrix ![]() with rank r such that
with rank r such that ![]() . Let
. Let ![]() be a
be a ![]() matrix with rank m such that
matrix with rank m such that ![]() ; then
; then ![]() has rank m. The
has rank m. The ![]() has rank k. By construction of H,
has rank k. By construction of H,
where ![]() . Since
. Since ![]() and
and ![]() ,
, ![]() lies in the column space of
lies in the column space of ![]() and can be written
and can be written
where ![]() is a k-dimensional vector. The common trends representation is written as
is a k-dimensional vector. The common trends representation is written as
![\begin{eqnarray*} \mb{y} _ t & = & \mb{y} _0 + \Psi (1)[\tilde{\bdelta } t + \sum _{i=0}^{t}\bepsilon _ i] + \Psi ^{*}(B)\bepsilon _ t \\ & = & \mb{y} _0 + \Psi (1)H[H^{-1}\tilde{\delta } t + H^{-1}\sum _{i=0}^{t}\bepsilon _ i] + \mb{a} _ t \\ & = & \mb{y} _0 + A\btau _ t + \mb{a} _ t \end{eqnarray*}](images/etsug_varmax0697.png)
and
where ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
Stock and Watson showed that the common trends representation expresses ![]() as a linear combination of m random walks (
as a linear combination of m random walks (![]() ) with drift
) with drift ![]() plus
plus ![]() components (
components (![]() .
.
Stock and Watson (1988) proposed statistics for common trends testing. The null hypothesis is that the k-dimensional time series ![]() has m common stochastic trends, where
has m common stochastic trends, where ![]() and the alternative is that it has s common trends, where
and the alternative is that it has s common trends, where ![]() . The test procedure of m versus s common stochastic trends is performed based on the first-order serial correlation matrix of
. The test procedure of m versus s common stochastic trends is performed based on the first-order serial correlation matrix of ![]() . Let
. Let ![]() be a
be a ![]() matrix orthogonal to the cointegrating matrix such that
matrix orthogonal to the cointegrating matrix such that ![]() and
and ![]() . Let
. Let ![]() and
and ![]() . Then
. Then
Combining the expression of ![]() and
and ![]() ,
,
![\begin{eqnarray*} \left[ \begin{array}{c} \mb{z} _ t \\ \mb{w} _ t \end{array} \right] & = & \left[ \begin{array}{c} \bbeta ’\mb{y} _0 \\ \bbeta _{\bot }^{'}\mb{y} _0 \end{array} \right] + \left[ \begin{array}{c} 0 \\ \bbeta _{\bot }^{'}\bdelta \end{array} \right] t + \left[ \begin{array}{c} 0 \\ \bbeta _{\bot }^{'}\Psi (1) \end{array} \right] \sum _{i=1}^ t\bepsilon _ i \\ & + & \left[ \begin{array}{c} \bbeta ’\Psi ^{*}(B) \\ \bbeta _{\bot }’\Psi ^{*}(B) \end{array} \right] \bepsilon _ t \end{eqnarray*}](images/etsug_varmax0716.png)
The Stock-Watson common trends test is performed based on the component ![]() by testing whether
by testing whether ![]() has rank m against rank s.
has rank m against rank s.
The following statements perform the Stock-Watson test for common trends:
proc iml;
sig = 100*i(2);
phi = {-0.2 0.1, 0.5 0.2, 0.8 0.7, -0.4 0.6};
call varmasim(y,phi) sigma=sig n=100 initial=0
seed=45876;
cn = {'y1' 'y2'};
create simul2 from y[colname=cn];
append from y;
quit;
data simul2;
set simul2;
date = intnx( 'year', '01jan1900'd, _n_-1 );
format date year4. ;
run;
proc varmax data=simul2;
model y1 y2 / p=2 cointtest=(sw);
run;
In Figure 35.51, the first column is the null hypothesis that ![]() has
has ![]() common trends; the second column is the alternative hypothesis that
common trends; the second column is the alternative hypothesis that ![]() has
has ![]() common trends; the third column contains the eigenvalues used for the test statistics; the fourth column contains the test
statistics using AR(p) filtering of the data. The table shows the output of the case
common trends; the third column contains the eigenvalues used for the test statistics; the fourth column contains the test
statistics using AR(p) filtering of the data. The table shows the output of the case ![]() .
.
The test statistic for testing for 2 versus 1 common trends is more negative (–35.1) than the critical value (–23.0). Therefore, the test rejects the null hypothesis, which means that the series has a single common trend.