The VARMAX Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues
Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues -
Examples

- References
-
Information Criterion After fitting some candidate models to the data, various model selection criteria (normalized by
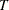 ) can be used to choose the appropriate model. The following list includes the Akaike information criterion (AIC), the corrected
Akaike information criterion (AICC), the final prediction error criterion (FPE), the Hannan-Quinn criterion (HQC), and the
Schwarz Bayesian criterion (SBC, also referred to as BIC):
) can be used to choose the appropriate model. The following list includes the Akaike information criterion (AIC), the corrected
Akaike information criterion (AICC), the final prediction error criterion (FPE), the Hannan-Quinn criterion (HQC), and the
Schwarz Bayesian criterion (SBC, also referred to as BIC):
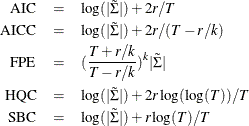
where r denotes the number of parameters estimated, k is the number of dependent variables,
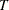 is the number of observations used to estimate the model, and
is the number of observations used to estimate the model, and 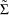 is the maximum likelihood estimate of
is the maximum likelihood estimate of 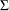 . When comparing models, choose the model with the smallest criterion values.
. When comparing models, choose the model with the smallest criterion values.
An example of the output was displayed in Figure 35.4.
-
Portmanteau
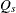 statistic The Portmanteau
statistic The Portmanteau 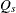 statistic is used to test whether correlation remains on the model residuals. The null hypothesis is that the residuals are
uncorrelated. Let
statistic is used to test whether correlation remains on the model residuals. The null hypothesis is that the residuals are
uncorrelated. Let 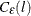 be the residual cross-covariance matrices,
be the residual cross-covariance matrices, 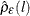 be the residual cross-correlation matrices as
be the residual cross-correlation matrices as
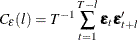
and
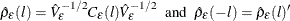
where
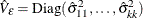 and
and 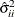 are the diagonal elements of
are the diagonal elements of 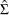 . The multivariate portmanteau test defined in Hosking (1980) is
. The multivariate portmanteau test defined in Hosking (1980) is
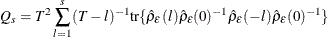
The statistic
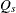 has approximately the chi-square distribution with
has approximately the chi-square distribution with 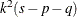 degrees of freedom. An example of the output is displayed in Figure 35.7.
degrees of freedom. An example of the output is displayed in Figure 35.7.
There are various ways to perform diagnostic checks for a univariate model. For details, see the section Testing for Nonlinear Dependence: Heteroscedasticity Tests in Chapter 8: The AUTOREG Procedure. An example of the output is displayed in Figure 35.8 and Figure 35.9.
-
Durbin-Watson (DW) statistics: The DW test statistics test for the first order autocorrelation in the residuals.
-
Jarque-Bera normality test: This test is helpful in determining whether the model residuals represent a white noise process. This tests the null hypothesis that the residuals have normality.
-
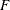 tests for autoregressive conditional heteroscedastic (ARCH) disturbances:
tests for autoregressive conditional heteroscedastic (ARCH) disturbances: 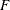 test statistics test for the heteroscedastic disturbances in the residuals. This tests the null hypothesis that the residuals
have equal covariances
test statistics test for the heteroscedastic disturbances in the residuals. This tests the null hypothesis that the residuals
have equal covariances
-
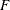 tests for AR disturbance: These test statistics are computed from the residuals of the univariate AR(1), AR(1,2), AR(1,2,3)
and AR(1,2,3,4) models to test the null hypothesis that the residuals are uncorrelated.
tests for AR disturbance: These test statistics are computed from the residuals of the univariate AR(1), AR(1,2), AR(1,2,3)
and AR(1,2,3,4) models to test the null hypothesis that the residuals are uncorrelated.