The VARMAX Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues
Missing ValuesVARMAX ModelDynamic Simultaneous Equations ModelingImpulse Response FunctionForecastingTentative Order SelectionVAR and VARX ModelingBayesian VAR and VARX ModelingVARMA and VARMAX ModelingModel Diagnostic ChecksCointegrationVector Error Correction ModelingI(2) ModelMultivariate GARCH ModelingOutput Data SetsOUT= Data SetOUTEST= Data SetOUTHT= Data SetOUTSTAT= Data SetPrinted OutputODS Table NamesODS GraphicsComputational Issues -
Examples

- References
Consider the following four-dimensional system of U.S. economic variables. Quarterly data for the years 1954 to 1987 are used (Lütkepohl 1993, Table E.3.).
title 'Analysis of U.S. Economic Variables';
data us_money;
date=intnx( 'qtr', '01jan54'd, _n_-1 );
format date yyq. ;
input y1 y2 y3 y4 @@;
y1=log(y1);
y2=log(y2);
label y1='log(real money stock M1)'
y2='log(GNP in bil. of 1982 dollars)'
y3='Discount rate on 91-day T-bills'
y4='Yield on 20-year Treasury bonds';
datalines;
450.9 1406.8 0.010800000 0.026133333
453.0 1401.2 0.0081333333 0.025233333
459.1 1418.0 0.0087000000 0.024900000
... more lines ...
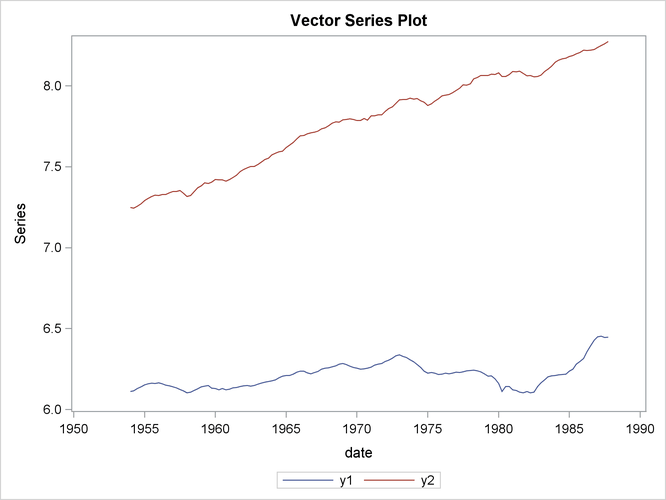
The following statements plot the series and proceed with the VARMAX procedure.
proc timeseries data=us_money vectorplot=series; id date interval=qtr; var y1 y2; run;
Output 35.1.1 shows the plot of the variables ![]() and
and ![]() .
.
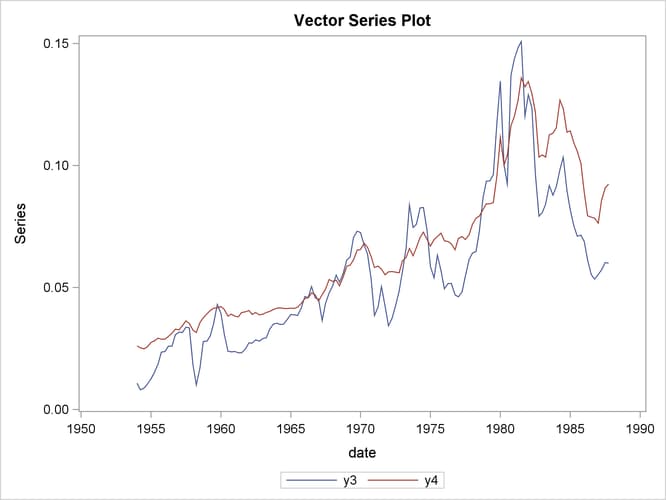
The following statements plot the variables ![]() and
and ![]() .
.
proc timeseries data=us_money vectorplot=series; id date interval=qtr; var y3 y4; run;
Output 35.1.2 shows the plot of the variables ![]() and
and ![]() .
.
proc varmax data=us_money;
id date interval=qtr;
model y1-y4 / p=2 lagmax=6 dftest
print=(iarr(3) estimates diagnose)
cointtest=(johansen=(iorder=2))
ecm=(rank=1 normalize=y1);
cointeg rank=1 normalize=y1 exogeneity;
run;
This example performs the Dickey-Fuller test for stationarity, the Johansen cointegrated test integrated order 2, and the exogeneity test. The VECM(2) is fit to the data. From the outputs shown in Output 35.1.5, you can see that the series has unit roots and is cointegrated in rank 1 with integrated order 1. The fitted VECM(2) is given as
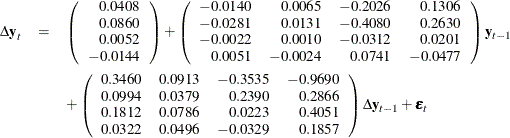
The ![]() prefixed to a variable name implies differencing.
prefixed to a variable name implies differencing.
Output 35.1.3 through Output 35.1.14 show the details. Output 35.1.3 shows the descriptive statistics.
Output 35.1.3: Descriptive Statistics
| Analysis of U.S. Economic Variables |
| Number of Observations | 136 |
|---|---|
| Number of Pairwise Missing | 0 |
| Simple Summary Statistics | |||||||
|---|---|---|---|---|---|---|---|
| Variable | Type | N | Mean | Standard Deviation |
Min | Max | Label |
| y1 | Dependent | 136 | 6.21295 | 0.07924 | 6.10278 | 6.45331 | log(real money stock M1) |
| y2 | Dependent | 136 | 7.77890 | 0.30110 | 7.24508 | 8.27461 | log(GNP in bil. of 1982 dollars) |
| y3 | Dependent | 136 | 0.05608 | 0.03109 | 0.00813 | 0.15087 | Discount rate on 91-day T-bills |
| y4 | Dependent | 136 | 0.06458 | 0.02927 | 0.02490 | 0.13600 | Yield on 20-year Treasury bonds |
Output 35.1.4 shows the output for Dickey-Fuller tests for the nonstationarity of each series. The null hypotheses is to test a unit root. All series have a unit root.
Output 35.1.4: Unit Root Tests
| Unit Root Test | |||||
|---|---|---|---|---|---|
| Variable | Type | Rho | Pr < Rho | Tau | Pr < Tau |
| y1 | Zero Mean | 0.05 | 0.6934 | 1.14 | 0.9343 |
| Single Mean | -2.97 | 0.6572 | -0.76 | 0.8260 | |
| Trend | -5.91 | 0.7454 | -1.34 | 0.8725 | |
| y2 | Zero Mean | 0.13 | 0.7124 | 5.14 | 0.9999 |
| Single Mean | -0.43 | 0.9309 | -0.79 | 0.8176 | |
| Trend | -9.21 | 0.4787 | -2.16 | 0.5063 | |
| y3 | Zero Mean | -1.28 | 0.4255 | -0.69 | 0.4182 |
| Single Mean | -8.86 | 0.1700 | -2.27 | 0.1842 | |
| Trend | -18.97 | 0.0742 | -2.86 | 0.1803 | |
| y4 | Zero Mean | 0.40 | 0.7803 | 0.45 | 0.8100 |
| Single Mean | -2.79 | 0.6790 | -1.29 | 0.6328 | |
| Trend | -12.12 | 0.2923 | -2.33 | 0.4170 | |
The Johansen cointegration rank test shows whether the series is integrated order either 1 or 2 as shown in Output 35.1.5. The last two columns in Output 35.1.5 explain the cointegration rank test with integrated order 1. The results indicate that there is the cointegrated relationship
with the cointegration rank 1 with respect to the 0.05 significance level because the test statistic of 20.6542 is smaller
than the critical value of 29.38. Now, look at the row associated with ![]() . Compare the test statistic value and critical value pairs such as (219.62395, 29.38), (89.21508, 15.34), and (27.32609,
3.84). There is no evidence that the series are integrated order 2 at the 0.05 significance level.
. Compare the test statistic value and critical value pairs such as (219.62395, 29.38), (89.21508, 15.34), and (27.32609,
3.84). There is no evidence that the series are integrated order 2 at the 0.05 significance level.
Output 35.1.5: Cointegration Rank Test
| Cointegration Rank Test for I(2) | ||||||
|---|---|---|---|---|---|---|
| r\k-r-s | 4 | 3 | 2 | 1 | Trace of I(1) |
Pr > Trace of I(1) |
| 0 | 384.6090 | 214.3790 | 107.9378 | 37.0252 | 55.9633 | 0.0072 |
| Pr > Trace of I(2) | 0.0000 | 0.0000 | 0.0000 | 0.0000 | ||
| 1 | 219.6239 | 89.2151 | 27.3261 | 20.6542 | 0.3775 | |
| Pr > Trace of I(2) | 0.0000 | 0.0000 | 0.0000 | |||
| 2 | 73.6178 | 22.1328 | 2.6477 | 0.9803 | ||
| Pr > Trace of I(2) | 0.0000 | 0.0000 | ||||
| 3 | 38.2943 | 0.0149 | 0.9031 | |||
| Pr > Trace of I(2) | 0.0000 | |||||
Output 35.1.6 shows the estimates of the long-run parameter, ![]() , and the adjustment coefficient,
, and the adjustment coefficient, ![]() .
.
Output 35.1.6: Cointegration Rank Test Continued
| Beta | ||||
|---|---|---|---|---|
| Variable | 1 | 2 | 3 | 4 |
| y1 | 1.00000 | 1.00000 | 1.00000 | 1.00000 |
| y2 | -0.46458 | -0.63174 | -0.69996 | -0.16140 |
| y3 | 14.51619 | -1.29864 | 1.37007 | -0.61806 |
| y4 | -9.35520 | 7.53672 | 2.47901 | 1.43731 |
| Alpha | ||||
|---|---|---|---|---|
| Variable | 1 | 2 | 3 | 4 |
| y1 | -0.01396 | 0.01396 | -0.01119 | 0.00008 |
| y2 | -0.02811 | -0.02739 | -0.00032 | 0.00076 |
| y3 | -0.00215 | -0.04967 | -0.00183 | -0.00072 |
| y4 | 0.00510 | -0.02514 | -0.00220 | 0.00016 |
Output 35.1.7 shows the estimates ![]() and
and ![]() .
.
Output 35.1.7: Cointegration Rank Test Continued
| Eta | ||||
|---|---|---|---|---|
| Variable | 1 | 2 | 3 | 4 |
| y1 | 52.74907 | 41.74502 | -20.80403 | 55.77415 |
| y2 | -49.10609 | -9.40081 | 98.87199 | 22.56416 |
| y3 | 68.29674 | -144.83173 | -27.35953 | 15.51142 |
| y4 | 121.25932 | 271.80496 | 85.85156 | -130.11599 |
| Xi | ||||
|---|---|---|---|---|
| Variable | 1 | 2 | 3 | 4 |
| y1 | -0.00842 | -0.00052 | -0.00208 | -0.00250 |
| y2 | 0.00141 | 0.00213 | -0.00736 | -0.00058 |
| y3 | -0.00445 | 0.00541 | -0.00150 | 0.00310 |
| y4 | -0.00211 | -0.00064 | -0.00130 | 0.00197 |
Output 35.1.8 shows that the VECM(2) is fit to the data. The ECM=(RANK=1) option produces the estimates of the long-run parameter, ![]() , and the adjustment coefficient,
, and the adjustment coefficient, ![]() .
.
Output 35.1.9 shows the parameter estimates in terms of the constant, the lag one coefficients (![]() ) contained in the
) contained in the ![]() estimates, and the coefficients associated with the lag one first differences (
estimates, and the coefficients associated with the lag one first differences (![]() ).
).
Output 35.1.9: Parameter Estimates Continued
| Constant | |
|---|---|
| Variable | Constant |
| y1 | 0.04076 |
| y2 | 0.08595 |
| y3 | 0.00518 |
| y4 | -0.01438 |
| Parameter Alpha * Beta' Estimates | ||||
|---|---|---|---|---|
| Variable | y1 | y2 | y3 | y4 |
| y1 | -0.01396 | 0.00648 | -0.20263 | 0.13059 |
| y2 | -0.02811 | 0.01306 | -0.40799 | 0.26294 |
| y3 | -0.00215 | 0.00100 | -0.03121 | 0.02011 |
| y4 | 0.00510 | -0.00237 | 0.07407 | -0.04774 |
| AR Coefficients of Differenced Lag | |||||
|---|---|---|---|---|---|
| DIF Lag | Variable | y1 | y2 | y3 | y4 |
| 1 | y1 | 0.34603 | 0.09131 | -0.35351 | -0.96895 |
| y2 | 0.09936 | 0.03791 | 0.23900 | 0.28661 | |
| y3 | 0.18118 | 0.07859 | 0.02234 | 0.40508 | |
| y4 | 0.03222 | 0.04961 | -0.03292 | 0.18568 | |
Output 35.1.10 shows the parameter estimates and their significance.
Output 35.1.10: Parameter Estimates Continued
| Model Parameter Estimates | ||||||
|---|---|---|---|---|---|---|
| Equation | Parameter | Estimate | Standard Error |
t Value | Pr > |t| | Variable |
| D_y1 | CONST1 | 0.04076 | 0.01418 | 2.87 | 0.0048 | 1 |
| AR1_1_1 | -0.01396 | 0.00495 | y1(t-1) | |||
| AR1_1_2 | 0.00648 | 0.00230 | y2(t-1) | |||
| AR1_1_3 | -0.20263 | 0.07191 | y3(t-1) | |||
| AR1_1_4 | 0.13059 | 0.04634 | y4(t-1) | |||
| AR2_1_1 | 0.34603 | 0.06414 | 5.39 | 0.0001 | D_y1(t-1) | |
| AR2_1_2 | 0.09131 | 0.07334 | 1.25 | 0.2154 | D_y2(t-1) | |
| AR2_1_3 | -0.35351 | 0.11024 | -3.21 | 0.0017 | D_y3(t-1) | |
| AR2_1_4 | -0.96895 | 0.20737 | -4.67 | 0.0001 | D_y4(t-1) | |
| D_y2 | CONST2 | 0.08595 | 0.01679 | 5.12 | 0.0001 | 1 |
| AR1_2_1 | -0.02811 | 0.00586 | y1(t-1) | |||
| AR1_2_2 | 0.01306 | 0.00272 | y2(t-1) | |||
| AR1_2_3 | -0.40799 | 0.08514 | y3(t-1) | |||
| AR1_2_4 | 0.26294 | 0.05487 | y4(t-1) | |||
| AR2_2_1 | 0.09936 | 0.07594 | 1.31 | 0.1932 | D_y1(t-1) | |
| AR2_2_2 | 0.03791 | 0.08683 | 0.44 | 0.6632 | D_y2(t-1) | |
| AR2_2_3 | 0.23900 | 0.13052 | 1.83 | 0.0695 | D_y3(t-1) | |
| AR2_2_4 | 0.28661 | 0.24552 | 1.17 | 0.2453 | D_y4(t-1) | |
| D_y3 | CONST3 | 0.00518 | 0.01608 | 0.32 | 0.7476 | 1 |
| AR1_3_1 | -0.00215 | 0.00562 | y1(t-1) | |||
| AR1_3_2 | 0.00100 | 0.00261 | y2(t-1) | |||
| AR1_3_3 | -0.03121 | 0.08151 | y3(t-1) | |||
| AR1_3_4 | 0.02011 | 0.05253 | y4(t-1) | |||
| AR2_3_1 | 0.18118 | 0.07271 | 2.49 | 0.0140 | D_y1(t-1) | |
| AR2_3_2 | 0.07859 | 0.08313 | 0.95 | 0.3463 | D_y2(t-1) | |
| AR2_3_3 | 0.02234 | 0.12496 | 0.18 | 0.8584 | D_y3(t-1) | |
| AR2_3_4 | 0.40508 | 0.23506 | 1.72 | 0.0873 | D_y4(t-1) | |
| D_y4 | CONST4 | -0.01438 | 0.00803 | -1.79 | 0.0758 | 1 |
| AR1_4_1 | 0.00510 | 0.00281 | y1(t-1) | |||
| AR1_4_2 | -0.00237 | 0.00130 | y2(t-1) | |||
| AR1_4_3 | 0.07407 | 0.04072 | y3(t-1) | |||
| AR1_4_4 | -0.04774 | 0.02624 | y4(t-1) | |||
| AR2_4_1 | 0.03222 | 0.03632 | 0.89 | 0.3768 | D_y1(t-1) | |
| AR2_4_2 | 0.04961 | 0.04153 | 1.19 | 0.2345 | D_y2(t-1) | |
| AR2_4_3 | -0.03292 | 0.06243 | -0.53 | 0.5990 | D_y3(t-1) | |
| AR2_4_4 | 0.18568 | 0.11744 | 1.58 | 0.1164 | D_y4(t-1) | |
Output 35.1.11 shows the innovation covariance matrix estimates, the various information criteria results, and the tests for white noise residuals. The residuals have significant correlations at lag 2 and 3. The Portmanteau test results into significant. These results show that a VECM(3) model might be better fit than the VECM(2) model is.
Output 35.1.11: Diagnostic Checks
| Covariances of Innovations | ||||
|---|---|---|---|---|
| Variable | y1 | y2 | y3 | y4 |
| y1 | 0.00005 | 0.00001 | -0.00001 | -0.00000 |
| y2 | 0.00001 | 0.00007 | 0.00002 | 0.00001 |
| y3 | -0.00001 | 0.00002 | 0.00007 | 0.00002 |
| y4 | -0.00000 | 0.00001 | 0.00002 | 0.00002 |
| Information Criteria | |
|---|---|
| AICC | -40.6284 |
| HQC | -40.4343 |
| AIC | -40.6452 |
| SBC | -40.1262 |
| FPEC | 2.23E-18 |
| Schematic Representation of Cross Correlations of Residuals |
|||||||
|---|---|---|---|---|---|---|---|
| Variable/Lag | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y1 | ++.. | .... | ++.. | .... | +... | ..-- | .... |
| y2 | ++++ | .... | .... | .... | .... | .... | .... |
| y3 | .+++ | .... | +.-. | ..++ | -... | .... | .... |
| y4 | .+++ | .... | .... | ..+. | .... | .... | .... |
| + is > 2*std error, - is < -2*std error, . is between | |||||||
| Portmanteau Test for Cross Correlations of Residuals |
|||
|---|---|---|---|
| Up To Lag | DF | Chi-Square | Pr > ChiSq |
| 3 | 16 | 53.90 | <.0001 |
| 4 | 32 | 74.03 | <.0001 |
| 5 | 48 | 103.08 | <.0001 |
| 6 | 64 | 116.94 | <.0001 |
Output 35.1.12 describes how well each univariate equation fits the data. The residuals for ![]() and
and ![]() are off from the normality. Except the residuals for
are off from the normality. Except the residuals for ![]() , there are no AR effects on other residuals. Except the residuals for
, there are no AR effects on other residuals. Except the residuals for ![]() , there are no ARCH effects on other residuals.
, there are no ARCH effects on other residuals.
Output 35.1.12: Diagnostic Checks Continued
| Univariate Model ANOVA Diagnostics | ||||
|---|---|---|---|---|
| Variable | R-Square | Standard Deviation |
F Value | Pr > F |
| y1 | 0.6754 | 0.00712 | 32.51 | <.0001 |
| y2 | 0.3070 | 0.00843 | 6.92 | <.0001 |
| y3 | 0.1328 | 0.00807 | 2.39 | 0.0196 |
| y4 | 0.0831 | 0.00403 | 1.42 | 0.1963 |
| Univariate Model White Noise Diagnostics | |||||
|---|---|---|---|---|---|
| Variable | Durbin Watson |
Normality | ARCH | ||
| Chi-Square | Pr > ChiSq | F Value | Pr > F | ||
| y1 | 2.13418 | 7.19 | 0.0275 | 1.62 | 0.2053 |
| y2 | 2.04003 | 1.20 | 0.5483 | 1.23 | 0.2697 |
| y3 | 1.86892 | 253.76 | <.0001 | 1.78 | 0.1847 |
| y4 | 1.98440 | 105.21 | <.0001 | 21.01 | <.0001 |
| Univariate Model AR Diagnostics | ||||||||
|---|---|---|---|---|---|---|---|---|
| Variable | AR1 | AR2 | AR3 | AR4 | ||||
| F Value | Pr > F | F Value | Pr > F | F Value | Pr > F | F Value | Pr > F | |
| y1 | 0.68 | 0.4126 | 2.98 | 0.0542 | 2.01 | 0.1154 | 2.48 | 0.0473 |
| y2 | 0.05 | 0.8185 | 0.12 | 0.8842 | 0.41 | 0.7453 | 0.30 | 0.8762 |
| y3 | 0.56 | 0.4547 | 2.86 | 0.0610 | 4.83 | 0.0032 | 3.71 | 0.0069 |
| y4 | 0.01 | 0.9340 | 0.16 | 0.8559 | 1.21 | 0.3103 | 0.95 | 0.4358 |
The PRINT=(IARR) option provides the VAR(2) representation in Output 35.1.13.
Output 35.1.13: Infinite Order AR Representation
| Infinite Order AR Representation | |||||
|---|---|---|---|---|---|
| Lag | Variable | y1 | y2 | y3 | y4 |
| 1 | y1 | 1.33208 | 0.09780 | -0.55614 | -0.83836 |
| y2 | 0.07125 | 1.05096 | -0.16899 | 0.54955 | |
| y3 | 0.17903 | 0.07959 | 0.99113 | 0.42520 | |
| y4 | 0.03732 | 0.04724 | 0.04116 | 1.13795 | |
| 2 | y1 | -0.34603 | -0.09131 | 0.35351 | 0.96895 |
| y2 | -0.09936 | -0.03791 | -0.23900 | -0.28661 | |
| y3 | -0.18118 | -0.07859 | -0.02234 | -0.40508 | |
| y4 | -0.03222 | -0.04961 | 0.03292 | -0.18568 | |
| 3 | y1 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| y2 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | |
| y3 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | |
| y4 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | |
Output 35.1.14 shows whether each variable is the weak exogeneity of other variables. The variable ![]() is not the weak exogeneity of other variables,
is not the weak exogeneity of other variables, ![]() ,
, ![]() , and
, and ![]() ; the variable
; the variable ![]() is not the weak exogeneity of other variables,
is not the weak exogeneity of other variables, ![]() ,
, ![]() , and
, and ![]() ; the variable
; the variable ![]() and
and ![]() are the weak exogeneity of other variables.
are the weak exogeneity of other variables.