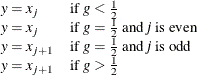The UNIVARIATE Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Missing ValuesRoundingDescriptive StatisticsCalculating the ModeCalculating PercentilesTests for LocationConfidence Limits for Parameters of the Normal DistributionRobust EstimatorsCreating Line Printer PlotsCreating High-Resolution GraphicsUsing the CLASS Statement to Create Comparative PlotsPositioning InsetsFormulas for Fitted Continuous DistributionsGoodness-of-Fit TestsKernel Density EstimatesConstruction of Quantile-Quantile and Probability PlotsInterpretation of Quantile-Quantile and Probability PlotsDistributions for Probability and Q-Q PlotsEstimating Shape Parameters Using Q-Q PlotsEstimating Location and Scale Parameters Using Q-Q PlotsEstimating Percentiles Using Q-Q PlotsInput Data SetsOUT= Output Data Set in the OUTPUT StatementOUTHISTOGRAM= Output Data SetOUTKERNEL= Output Data SetOUTTABLE= Output Data SetTables for Summary StatisticsODS Table NamesODS Tables for Fitted DistributionsODS GraphicsComputational Resources
Missing ValuesRoundingDescriptive StatisticsCalculating the ModeCalculating PercentilesTests for LocationConfidence Limits for Parameters of the Normal DistributionRobust EstimatorsCreating Line Printer PlotsCreating High-Resolution GraphicsUsing the CLASS Statement to Create Comparative PlotsPositioning InsetsFormulas for Fitted Continuous DistributionsGoodness-of-Fit TestsKernel Density EstimatesConstruction of Quantile-Quantile and Probability PlotsInterpretation of Quantile-Quantile and Probability PlotsDistributions for Probability and Q-Q PlotsEstimating Shape Parameters Using Q-Q PlotsEstimating Location and Scale Parameters Using Q-Q PlotsEstimating Percentiles Using Q-Q PlotsInput Data SetsOUT= Output Data Set in the OUTPUT StatementOUTHISTOGRAM= Output Data SetOUTKERNEL= Output Data SetOUTTABLE= Output Data SetTables for Summary StatisticsODS Table NamesODS Tables for Fitted DistributionsODS GraphicsComputational Resources -
Examples
 Computing Descriptive Statistics for Multiple VariablesCalculating ModesIdentifying Extreme Observations and Extreme ValuesCreating a Frequency TableCreating Plots for Line Printer OutputAnalyzing a Data Set With a FREQ VariableSaving Summary Statistics in an OUT= Output Data SetSaving Percentiles in an Output Data SetComputing Confidence Limits for the Mean, Standard Deviation, and VarianceComputing Confidence Limits for Quantiles and PercentilesComputing Robust EstimatesTesting for LocationPerforming a Sign Test Using Paired DataCreating a HistogramCreating a One-Way Comparative HistogramCreating a Two-Way Comparative HistogramAdding Insets with Descriptive StatisticsBinning a HistogramAdding a Normal Curve to a HistogramAdding Fitted Normal Curves to a Comparative HistogramFitting a Beta CurveFitting Lognormal, Weibull, and Gamma CurvesComputing Kernel Density EstimatesFitting a Three-Parameter Lognormal CurveAnnotating a Folded Normal CurveCreating Lognormal Probability PlotsCreating a Histogram to Display Lognormal FitCreating a Normal Quantile PlotAdding a Distribution Reference LineInterpreting a Normal Quantile PlotEstimating Three Parameters from Lognormal Quantile PlotsEstimating Percentiles from Lognormal Quantile PlotsEstimating Parameters from Lognormal Quantile PlotsComparing Weibull Quantile PlotsCreating a Cumulative Distribution PlotCreating a P-P Plot
Computing Descriptive Statistics for Multiple VariablesCalculating ModesIdentifying Extreme Observations and Extreme ValuesCreating a Frequency TableCreating Plots for Line Printer OutputAnalyzing a Data Set With a FREQ VariableSaving Summary Statistics in an OUT= Output Data SetSaving Percentiles in an Output Data SetComputing Confidence Limits for the Mean, Standard Deviation, and VarianceComputing Confidence Limits for Quantiles and PercentilesComputing Robust EstimatesTesting for LocationPerforming a Sign Test Using Paired DataCreating a HistogramCreating a One-Way Comparative HistogramCreating a Two-Way Comparative HistogramAdding Insets with Descriptive StatisticsBinning a HistogramAdding a Normal Curve to a HistogramAdding Fitted Normal Curves to a Comparative HistogramFitting a Beta CurveFitting Lognormal, Weibull, and Gamma CurvesComputing Kernel Density EstimatesFitting a Three-Parameter Lognormal CurveAnnotating a Folded Normal CurveCreating Lognormal Probability PlotsCreating a Histogram to Display Lognormal FitCreating a Normal Quantile PlotAdding a Distribution Reference LineInterpreting a Normal Quantile PlotEstimating Three Parameters from Lognormal Quantile PlotsEstimating Percentiles from Lognormal Quantile PlotsEstimating Parameters from Lognormal Quantile PlotsComparing Weibull Quantile PlotsCreating a Cumulative Distribution PlotCreating a P-P Plot - References
The UNIVARIATE procedure automatically computes the 1st, 5th, 10th, 25th, 50th, 75th, 90th, 95th, and 99th percentiles (quantiles), as well as the minimum and maximum of each analysis variable. To compute percentiles other than these default percentiles, use the PCTLPTS= and PCTLPRE= options in the OUTPUT statement.
You can specify one of five definitions for computing the percentiles with the PCTLDEF= option. Let ![]() be the number of nonmissing values for a variable, and let
be the number of nonmissing values for a variable, and let ![]() represent the ordered values of the variable. Let the
represent the ordered values of the variable. Let the ![]() th percentile be
th percentile be ![]() , set
, set ![]() , and let
, and let
where ![]() is the integer part of np, and
is the integer part of np, and ![]() is the fractional part of np. Then the PCTLDEF= option defines the
is the fractional part of np. Then the PCTLDEF= option defines the ![]() th percentile,
th percentile, ![]() , as described in the following table.
, as described in the following table.
|
PCTLDEF |
Description |
Formula |
|---|---|---|
|
1 |
weighted average at |
|
|
where |
||
|
2 |
observation numbered closest to np |
|
|
3 |
empirical distribution function |
|
|
4 |
weighted average aimed |
|
|
at |
where |
|
|
5 |
empirical distribution function with averaging |
|
When you use a WEIGHT statement, the percentiles are computed differently. The 100![]() th weighted percentile
th weighted percentile ![]() is computed from the empirical distribution function with averaging:
is computed from the empirical distribution function with averaging:
![\[ y = \left\{ \begin{array}{cl} x_1 & \mbox{if} \ w_1 > pW \\ \frac{1}{2} ( x_ i + x_{i+1} ) & \mbox{if} \sum _{j=1}^{i} w_ j = pW \\ x_{i+1} & \mbox{if} \sum _{j=1}^{i} w_ j < pW < \sum _{j=1}^{i+1} w_ j \end{array} \right. \]](images/procstat_univariate0194.png)
where ![]() is the weight associated with
is the weight associated with ![]() and
and ![]() is the sum of the weights.
is the sum of the weights.
Note that the PCTLDEF= option is not applicable when a WEIGHT statement is used. However, in this case, if all the weights are identical, the weighted percentiles are the same as the percentiles that would be computed without a WEIGHT statement and with PCTLDEF=5.
You can use the CIPCTLNORMAL option to request confidence limits for percentiles, assuming the data are normally distributed.
These limits are described in Section 4.4.1 of Hahn and Meeker (1991). When ![]() , the two-sided
, the two-sided ![]() confidence limits for the
confidence limits for the ![]() th percentile are
th percentile are
where ![]() is the sample size. When
is the sample size. When ![]() , the two-sided
, the two-sided ![]() confidence limits for the
confidence limits for the ![]() th percentile are
th percentile are
One-sided ![]() confidence bounds are computed by replacing
confidence bounds are computed by replacing ![]() by
by ![]() in the appropriate preceding equation. The factor
in the appropriate preceding equation. The factor ![]() is related to the noncentral
is related to the noncentral ![]() distribution and is described in Owen and Hua (1977) and Odeh and Owen (1980). See Example 4.10.
distribution and is described in Owen and Hua (1977) and Odeh and Owen (1980). See Example 4.10.
You can use the CIPCTLDF option to request distribution-free confidence limits for percentiles. In particular, it is not necessary
to assume that the data are normally distributed. These limits are described in Section 5.2 of Hahn and Meeker (1991). The two-sided ![]() confidence limits for the
confidence limits for the ![]() th percentile are
th percentile are
where ![]() is the
is the ![]() th order statistic when the data values are arranged in increasing order:
th order statistic when the data values are arranged in increasing order:
The lower rank ![]() and upper rank
and upper rank ![]() are integers that are symmetric (or nearly symmetric) around
are integers that are symmetric (or nearly symmetric) around ![]() , where
, where ![]() is the integer part of
is the integer part of ![]() and
and ![]() is the sample size. Furthermore,
is the sample size. Furthermore, ![]() and
and ![]() are chosen so that
are chosen so that ![]() and
and ![]() are as close to
are as close to ![]() as possible while satisfying the coverage probability requirement,
as possible while satisfying the coverage probability requirement,
where ![]() is the cumulative binomial probability,
is the cumulative binomial probability,
In some cases, the coverage requirement cannot be met, particularly when ![]() is small and
is small and ![]() is near 0 or 1. To relax the requirement of symmetry, you can specify CIPCTLDF(TYPE = ASYMMETRIC). This option requests symmetric
limits when the coverage requirement can be met, and asymmetric limits otherwise.
is near 0 or 1. To relax the requirement of symmetry, you can specify CIPCTLDF(TYPE = ASYMMETRIC). This option requests symmetric
limits when the coverage requirement can be met, and asymmetric limits otherwise.
If you specify CIPCTLDF(TYPE = LOWER), a one-sided ![]() lower confidence bound is computed as
lower confidence bound is computed as ![]() , where
, where ![]() is the largest integer that satisfies the inequality
is the largest integer that satisfies the inequality
with ![]() . Likewise, if you specify CIPCTLDF(TYPE = UPPER), a one-sided
. Likewise, if you specify CIPCTLDF(TYPE = UPPER), a one-sided ![]() lower confidence bound is computed as
lower confidence bound is computed as ![]() , where
, where ![]() is the largest integer that satisfies the inequality
is the largest integer that satisfies the inequality
Note that confidence limits for percentiles are not computed when a WEIGHT statement is specified. See Example 4.10.