The GLIMMIX Procedure
-
Overview

-
Getting Started

-
Syntax
 PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function
PROC GLIMMIX StatementBY StatementCLASS StatementCODE StatementCONTRAST StatementCOVTEST StatementEFFECT StatementESTIMATE StatementFREQ StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementPARMS StatementRANDOM StatementSLICE StatementSTORE StatementWEIGHT StatementProgramming StatementsUser-Defined Link or Variance Function -
Details
 Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance ("Sandwich") EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics
Generalized Linear Models TheoryGeneralized Linear Mixed Models TheoryGLM Mode or GLMM ModeStatistical Inference for Covariance ParametersDegrees of Freedom MethodsEmpirical Covariance ("Sandwich") EstimatorsExploring and Comparing Covariance MatricesProcessing by SubjectsRadial Smoothing Based on Mixed ModelsOdds and Odds Ratio EstimationParameterization of Generalized Linear Mixed ModelsResponse-Level Ordering and ReferencingComparing the GLIMMIX and MIXED ProceduresSingly or Doubly Iterative FittingDefault Estimation TechniquesDefault OutputNotes on Output StatisticsODS Table NamesODS Graphics -
Examples
 Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey Data
Binomial Counts in Randomized BlocksMating Experiment with Crossed Random EffectsSmoothing Disease Rates; Standardized Mortality RatiosQuasi-likelihood Estimation for Proportions with Unknown DistributionJoint Modeling of Binary and Count DataRadial Smoothing of Repeated Measures DataIsotonic Contrasts for Ordered AlternativesAdjusted Covariance Matrices of Fixed EffectsTesting Equality of Covariance and Correlation MatricesMultiple Trends Correspond to Multiple Extrema in Profile LikelihoodsMaximum Likelihood in Proportional Odds Model with Random EffectsFitting a Marginal (GEE-Type) ModelResponse Surface Comparisons with Multiplicity AdjustmentsGeneralized Poisson Mixed Model for Overdispersed Count DataComparing Multiple B-SplinesDiallel Experiment with Multimember Random EffectsLinear Inference Based on Summary DataWeighted Multilevel Model for Survey Data - References
Some restrictions and limitations for models that contain constructed effects are in place with the GLIMMIX procedure. Also, you should be aware of some special defaults and handling that apply only when the model contains constructed fixed and/or random effects.
-
Constructed effects can be used in the MODEL and RANDOM statements but not to specify SUBJECT= or GROUP= effects.
-
Computed variables are not supported in the specification of a constructed effect. All variables needed to form the collection of columns for a constructed effect must be in the data set.
-
You cannot use constructed effects that comprise continuous variables or interactions with other constructed effects as the LSMEANS or LSMESTIMATE effect.
-
The calculation of quantities that depend on least squares means, such as odds ratios in the "Odds Ratio Estimates" table, is not possible if the model contains fixed effects that consist of more than one constructed effects, unless all constructed effects are of spline type. For example, least squares means computations are not possible in the following model because the
MM_AB*cvarseffect contains two constructed effects:proc glimmix; class A B C; effect MM_AB = MM(A B); effect cvars = COLLECTION(x1 x2 x3); model y = C MM_AB*cvars; run;
-
If the MODEL or RANDOM statement contains constructed effects, the default degrees-of-freedom method for mixed models is DDFM= KENWARDROGER. The containment degrees-of-freedom method (DDFM= CONTAIN) is not available in these models.
-
If the model contains fixed spline effects, least squares means are computed at the average spline coefficients across the usable data, possibly further averaged over levels of CLASS variables that interact with the spline effects in the model. You can use the AT option in the LSMEANS and LSMESTIMATE statements to construct the splines for particular values of the covariates involved. Consider, for example, the following statements:
proc glimmix; class A; effect spl = spline(x); model y = A spl; lsmeans A; lsmeans A / at means; lsmeans A / at x=0.4; run;
Suppose that the
spleffect contributes seven columns![$[\mb{s}_1,\cdots ,\mb{s}_7]$](images/statug_glimmix0908.png) to the
to the 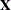 matrix. The least squares means coefficients for the
matrix. The least squares means coefficients for the spleffect in the first LSMEANS statement are![$[\overline{s}_1,\cdots ,\overline{s}_7]$](images/statug_glimmix0909.png) with the averages taken across the observations used in the analysis. The second LSMEANS
statement computes the spline coefficient at the average value of
with the averages taken across the observations used in the analysis. The second LSMEANS
statement computes the spline coefficient at the average value of x:![$[s(\overline{x})_1,\cdots ,s(\overline{x})_7]$](images/statug_glimmix0910.png) . The final LSMEANS
statement uses
. The final LSMEANS
statement uses ![$[s(0.4)_1,\cdots ,s(0.4)_7]$](images/statug_glimmix0911.png) . Using the AT option for least squares means calculations with spline effects can resolve inestimability issues.
. Using the AT option for least squares means calculations with spline effects can resolve inestimability issues.
-
Using a spline effect with B-spline basis in the RANDOM statement is not the same as using a penalized B-spline (P-spline) through the TYPE=PSPLINE option in the RANDOM statement. The following statement constructs a penalized B-spline by using mixed model methodology:
random x / type=pspline;
The next set of statements defines a set of B-spline columns in the
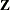 matrix with uncorrelated random effects and homogeneous variance:
matrix with uncorrelated random effects and homogeneous variance:
effect bspline = spline(x); random bspline / type=vc;
This does not lead to a properly penalized fit. See the documentation on TYPE=PSPLINE about the construction of penalties for B-splines through the covariance matrix of random effects.