The GLIMMIX Procedure

Model Options

ALPHA=number

requests that a t-type confidence interval be constructed for each of the fixed-effects parameters with confidence level 1 – number. The value of number must be between 0 and 1; the default is 0.05.

CHISQ

requests that chi-square tests be performed for all specified effects in addition to the F tests. Type III tests are the default; you can produce the Type I and Type II tests by using the HTYPE= option.

CL

requests that t-type confidence limits be constructed for each of the fixed-effects parameter estimates. The confidence level is 0.95 by default; this can be changed with the ALPHA= option.

CORRB

produces the correlation matrix from the approximate covariance matrix of the fixed-effects parameter estimates.

COVB<(DETAILS)>

produces the approximate variance-covariance matrix of the fixed-effects parameter estimates 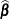$\widehat{\bbeta }$. In a generalized linear mixed model this matrix typically takes the form 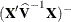$(\bX ’\widehat{\bV }^{-1}\bX )^{-}$ and can be obtained by sweeping the mixed model equations; see the section Estimated Precision of Estimates. In a model without random effects, it is obtained from the inverse of the observed or expected Hessian matrix. Which Hessian is used in the computation depends on whether the procedure is in scoring mode (see the SCORING= option in the PROC GLIMMIX statement) and whether the EXPHESSIAN option is in effect. Note that if you use EMPIRICAL= or DDFM= KENWARDROGER, the matrix displayed by the COVB option is the empirical (sandwich) estimator or the adjusted estimator, respectively.

The DETAILS suboption of the COVB option enables you to obtain a table of statistics about the covariance matrix of the fixed effects. If an adjusted estimator is used because of the EMPIRICAL= or DDFM= KENWARDROGER option, the GLIMMIX procedure displays statistics for the adjusted and unadjusted estimators as well as statistics comparing them. This enables you to diagnose, for example, changes in rank (because of an insufficient number of subjects for the empirical estimator) and to assess the extent of the covariance adjustment. In addition, the GLIMMIX procedure then displays the unadjusted (=model-based) covariance matrix of the fixed-effects parameter estimates. For more details, see the section Exploring and Comparing Covariance Matrices.

COVBI

produces the inverse of the approximate covariance matrix of the fixed-effects parameter estimates.

DDF=value-list
DF=value-list

enables you to specify your own denominator degrees of freedom for the fixed effects. The value-list specification is a list of numbers or missing values (.) separated by commas. The degrees of freedom should be listed in the order in which the effects appear in the "Type III Tests of Fixed Effects" table. If you want to retain the default degrees of freedom for a particular effect, use a missing value for its location in the list. For example, the statement assigns 3 denominator degrees of freedom to A and 4.7 to A*B, while those for B remain the same: 

model Y = A B A*B / ddf=3,.,4.7;

If you select a degrees-of-freedom method with the DDFM= option, then nonmissing, positive values in value-list override the degrees of freedom for the particular effect. For example, the statement assigns 3 and 6 denominator degrees of freedom in the test of the A main effect and the A*B interaction, respectively: 

model Y = A B A*B / ddf=3,.,6  ddfm=Satterth;

The denominator degrees of freedom for the test for the B effect are determined from a Satterthwaite approximation.

Note that the DDF= and DDFM= options determine the degrees of freedom in the "Type I Tests of Fixed Effects," "Type II Tests of Fixed Effects," and "Type III Tests of Fixed Effects" tables. These degrees of freedom are also used in determining the degrees of freedom in tests and confidence intervals from the CONTRAST , ESTIMATE , LSMEANS , and LSMESTIMATE statements. Exceptions from this rule are noted in the documentation for the respective statements.

DDFM=method

specifies the method for computing the denominator degrees of freedom for the tests of fixed effects that result from the MODEL, CONTRAST , ESTIMATE , LSMEANS , and LSMESTIMATE statements.

You can specify the following methods:

BETWITHIN
BW

assigns within-subject degrees of freedom to a fixed effect if the fixed effect changes within a subject, and between-subject degrees of freedom otherwise. This method is the default for models with only R-side random effects and a SUBJECT= option. Computational details can be found in the section Degrees of Freedom Methods.

CONTAIN
CON

invokes the containment method to compute denominator degrees of freedom. This method is the default when the model contains G-side random effects. Computational details can be found in the section Degrees of Freedom Methods.

KENWARDROGER<(FIRSTORDER)>
KENROGER<(FIRSTORDER)>
KR<(FIRSTORDER)>

applies the (prediction) standard error and degrees-of-freedom correction detailed by Kenward and Roger (1997). This approximation involves adjusting the estimated variance-covariance matrix of the fixed and random effects in a manner similar to that of Prasad and Rao (1990); Harville and Jeske (1992); Kackar and Harville (1984). Satterthwaite-type degrees of freedom are then computed based on this adjustment. Computational details can be found in the section Degrees of Freedom Methods.

KENWARDROGER2
KENROGER2
KR2

applies the (prediction) standard error and degrees-of-freedom correction that are detailed by Kenward and Roger (2009). This correction further reduces the precision estimator bias for the fixed and random effects under nonlinear covariance structures. Computational details can be found in the section Degrees of Freedom Methods.

NONE

specifies that no denominator degrees of freedom be applied. PROC GLIMMIX then essentially assumes that infinite degrees of freedom are available in the calculation of p-values. The p-values for t tests are then identical to p-values that are derived from the standard normal distribution. In the case of F tests, the p-values are equal to those of chi-square tests that are determined as follows: if 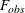$F_{\mathit{obs}}$ is the observed value of the F test with l numerator degrees of freedom, then

\[ p = \mr{Pr}\{ F_{l,\infty } > F_{\mathit{obs}} \} = \mr{Pr}\{ \chi ^2_ l > l F_{\mathit{obs}} \} \]

Regardless of the DDFM= method, you can obtain these chi-square p-values with the CHISQ option in the MODEL statement.

RESIDUAL
RES

performs all tests by using the residual degrees of freedom, 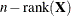$n - \mr{rank}(\mb{X})$, where n is the sum of the frequencies of observations or the sum of frequencies of event/trials pairs. This method is the default degrees of freedom method for GLMs and overdispersed GLMs.

SATTERTHWAITE
SAT

performs a general Satterthwaite approximation for the denominator degrees of freedom in a generalized linear mixed model. This method is a generalization of the techniques that are described in Giesbrecht and Burns (1985); McLean and Sanders (1988); Fai and Cornelius (1996). The method can also include estimated random effects. Computational details can be found in the section Degrees of Freedom Methods.

When the asymptotic variance matrix of the covariance parameters is found to be singular, a generalized inverse is used. Covariance parameters with zero variance then do not contribute to the degrees of freedom adjustment for DDFM=SATTERTH and DDFM=KENWARDROGER, and a message is written to the log.

DISTRIBUTION=keyword
DIST=keyword
D=keyword
ERROR=keyword
E=keyword

specifies the built-in (conditional) probability distribution of the data. If you specify the DIST= option and you do not specify a user-defined link function, a default link function is chosen according to the following table. If you do not specify a distribution, the GLIMMIX procedure defaults to the normal distribution for continuous response variables and to the multinomial distribution for classification or character variables, unless the events/trial syntax is used in the MODEL statement. If you choose the events/trial syntax, the GLIMMIX procedure defaults to the binomial distribution.

Table 44.12 lists the values of the DIST= option and the corresponding default link functions. For the case of generalized linear models with these distributions, you can find expressions for the log-likelihood functions in the section Maximum Likelihood.

Table 44.12: Keyword Values of the DIST= Option

   

Default Link

Numeric

DIST=

Distribution

Function

Value

BETA

beta

logit

12

BINARY

binary

logit

4

BINOMIAL | BIN | B

binomial

logit

3

EXPONENTIAL | EXPO

exponential

log

9

GAMMA | GAM

gamma

log

5

GAUSSIAN | G | NORMAL | N

normal

identity

1

GEOMETRIC | GEOM

geometric

log

8

INVGAUSS | IGAUSSIAN | IG

inverse Gaussian

inverse squared

6

   

(power(–2) )

 

LOGNORMAL | LOGN

lognormal

identity

11

MULTINOMIAL | MULTI | MULT

multinomial

cumulative logit

NA

NEGBINOMIAL | NEGBIN | NB

negative binomial

log

7

POISSON | POI | P

Poisson

log

2

TCENTRAL | TDIST | T

t

identity

10

BYOBS(variable)

multivariate

varied

NA


Note that the PROC GLIMMIX default link for the gamma or exponential distribution is not the canonical link (the reciprocal link).

The numeric value in the last column of Table 44.12 can be used in combination with DIST=BYOBS. The BYOBS(variable) syntax designates a variable whose value identifies the distribution to which an observation belongs. If the variable is numeric, its values must match values in the last column of Table 44.12. If the variable is not numeric, an observation’s distribution is identified by the first four characters of the distribution’s name in the leftmost column of the table. Distributions whose numeric value is "NA" cannot be used with DIST=BYOBS.

If the variable in BYOBS(variable) is a data set variable, it can also be used in the CLASS statement of the GLIMMIX procedure. For example, this provides a convenient method to model multivariate data jointly while varying fixed-effects components across outcomes. Assume that, for example, for each patient, a count and a continuous outcome were observed; the count data are modeled as Poisson data and the continuous data are modeled as gamma variates. The following statements fit a Poisson and a gamma regression model simultaneously: 

proc sort data=yourdata;
   by patient;
run;
data yourdata;
   set yourdata;
   by patient;
   if first.patient then dist='POIS' else dist='GAMM';
run;
proc glimmix data=yourdata;
   class treatment dist;
   model y = dist treatment*dist / dist=byobs(dist);
run;

The two models have separate intercepts and treatment effects. To correlate the outcomes, you can share a random effect between the observations from the same patient: 

proc glimmix data=yourdata;
   class treatment dist patient;
   model y = dist treatment*dist / dist=byobs(dist);
   random intercept / subject=patient;
run;

Or, you could use an R-side correlation structure: 

proc glimmix data=yourdata;
   class treatment dist patient;
   model y = dist treatment*dist / dist=byobs(dist);
   random _residual_ / subject=patient type=un;
run;

Although DIST=BYOBS(variable) is used to model multivariate data, you only need a single response variable in PROC GLIMMIX. The responses are in "univariate" form. This allows, for example, different missing value patterns across the responses. It does, however, require that all response variables be numeric.

The default links that are assigned when DIST=BYOBS is in effect correspond to the respective default links in Table 44.12.

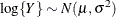When you choose DIST=LOGNORMAL, the GLIMMIX procedure models the logarithm of the response variable as a normal random variable. That is, the mean and variance are estimated on the logarithmic scale, assuming a normal distribution, $\log \{ Y\} \sim N(\mu ,\sigma ^2)$. This enables you to draw on options that require a distribution in the exponential family—for example, by using a scoring algorithm in a GLM. 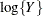To convert means and variances for $\log \{ Y\} $ into those of Y, use the relationships

\begin{align*} \mr{E}[Y] & = \exp \{ \mu \} \sqrt {\omega } \\ \mr{Var}[Y] & = \exp \{ 2\mu \} \omega (\omega -1) \\ \omega & = \exp \{ \sigma ^2\} \end{align*}

The DIST=T option models the data as a shifted and scaled central t variable. This enables you to model data with heavy-tailed distributions. If Y denotes the response and X has a 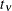$t_{\nu }$ distribution with $\nu $ degrees of freedom, then PROC GLIMMIX models

\[ Y = \mu + \sqrt {\phi } X \]

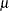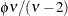In this parameterization, Y has mean $\mu $ and variance $\phi \nu /(\nu -2)$.

By default, 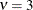$\nu =3$. You can supply different degrees of freedom for the t variate as in the following statements: 

proc glimmix;
   class a b;
   model y = b x b*x / dist=tcentral(9.6);
   random a;
run;

The GLIMMIX procedure does not accept values for the degrees of freedom parameter less than 3.0. If the t distribution is used with the DIST=BYOBS(variable) specification, the degrees of freedom are fixed at 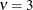$\nu = 3$. For mixed models where parameters are estimated based on linearization, choosing DIST=T instead of DIST=NORMAL affects only the residual variance, which decreases by the factor 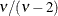$\nu /(\nu -2)$.

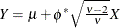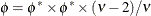Note that in SAS 9.1, the GLIMMIX procedure modeled $Y = \mu + \phi ^* \sqrt {\frac{\nu -2}{\nu }} X$. The scale parameter of the parameterizations are related as $\phi = \phi ^* \times \phi ^* \times (\nu -2)/\nu $.

The DIST=BETA option implements the parameterization of the beta distribution in Ferrari and Cribari-Neto (2004). If Y has a 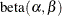$\mr{beta}(\alpha ,\beta )$ density, so that $\mr{E}[Y] = \mu = \alpha /(\alpha +\beta )$, this parameterization uses the variance function 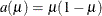$a(\mu ) = \mu (1-\mu )$ and $\mr{Var}[Y] = a(\mu )/(1+\phi )$.

See the section Maximum Likelihood for the log likelihoods of the distributions fitted by the GLIMMIX procedure.

E

requests that Type I, Type II, and Type III $\mb{L}$ matrix coefficients be displayed for all specified effects.

E1 | EI

requests that Type I $\mb{L}$ matrix coefficients be displayed for all specified effects.

E2 | EII

requests that Type II $\mb{L}$ matrix coefficients be displayed for all specified effects.

E3 | EIII

requests that Type III $\mb{L}$ matrix coefficients be displayed for all specified effects.

HTYPE=value-list

indicates the type of hypothesis test to perform on the fixed effects. Valid entries for values in the value-list are 1, 2, and 3, corresponding to Type I, Type II, and Type III tests. The default value is 3. You can specify several types by separating the values with a comma or a space. The ODS table names are "Tests1," "Tests2," and "Tests3" for the Type I, Type II, and Type III tests, respectively.

INTERCEPT

adds a row to the tables for Type I, II, and III tests corresponding to the overall intercept.

LINK=keyword

specifies the link function in the generalized linear mixed model. The keywords and their associated built-in link functions are shown in Table 44.13.

Table 44.13: Built-in Link Functions of the GLIMMIX Procedure

 

Link

 

Numeric

LINK=

Function

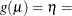
$g(\mu ) =\eta = $

Value

CUMCLL | CCLL

cumulative

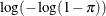
$\log (-\log (1-\pi ))$

NA
 

complementary log-log

   

CUMLOGIT | CLOGIT

cumulative logit

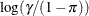
$\log (\gamma /(1-\pi ))$

NA

CUMLOGLOG

cumulative log-log

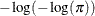
$-\log (-\log (\pi ))$

NA

CUMPROBIT | CPROBIT

cumulative probit

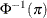
$\Phi ^{-1}(\pi )$

NA

CLOGLOG | CLL

complementary log-log

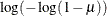
$\log (-\log (1-\mu ))$

5

GLOGIT | GENLOGIT

generalized logit

 

NA

IDENTITY | ID

identity

$\mu $

1

LOG

log

$\log (\mu )$

4

LOGIT

logit

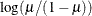
$\log (\mu /(1-\mu ))$

2

LOGLOG

log-log

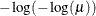
$-\log (-\log (\mu ))$

6

PROBIT

probit

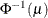
$\Phi ^{-1}(\mu )$

3

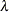POWER($\lambda $) | POW($\lambda $)

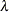power with exponent 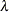$\lambda $= number

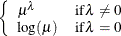
$\left\{ \begin{array}{ll} \mu ^{\lambda } & \mr{if } \, \lambda \not= 0 \\ \log (\mu ) & \mr{if } \, \lambda = 0 \end{array} \right.$

NA

POWERMINUS2

power with exponent -2

$1/\mu ^2$

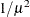
8

RECIPROCAL | INVERSE

reciprocal

$ 1/\mu $

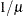
7

BYOBS(variable)

varied

varied

NA


For the probit and cumulative probit links, 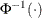$\Phi ^{-1}(\cdot )$ denotes the quantile function of the standard normal distribution. For the other cumulative links, $\pi $ denotes a cumulative category probability. The cumulative and generalized logit link functions are appropriate only for the multinomial distribution. When you choose a cumulative link function, PROC GLIMMIX assumes that the data are ordinal. When you specify LINK=GLOGIT, the GLIMMIX procedure assumes that the data are nominal (not ordered).

The numeric value in the rightmost column of Table 44.13 can be used in conjunction with LINK=BYOBS(variable). This syntax designates a variable whose values identify the link function associated with an observation. If the variable is numeric, its values must match those in the last column of Table 44.13. If the variable is not numeric, an observation’s link function is determined by the first four characters of the link’s name in the first column. Those link functions whose numeric value is "NA" cannot be used with LINK=BYOBS(variable).

You can define your own link function through programming statements. See the section User-Defined Link or Variance Function for more information about how to specify a link function. If a user-defined link function is in effect, the specification in the LINK= option is ignored. If you specify neither the LINK= option nor a user-defined link function, then the default link function is chosen according to Table 44.12.

LWEIGHT=FIRSTORDER | FIRO
LWEIGHT=NONE
LWEIGHT=VAR

determines how weights are used in constructing the coefficients for Type I through Type III $\mb{L}$ matrices. The default is LWEIGHT=VAR, and the values of the WEIGHT variable are used in forming crossproduct matrices. If you specify LWEIGHT=FIRO, the weights incorporate the WEIGHT variable as well as the first-order weights of the linearized model. For LWEIGHT=NONE, the $\bL $ matrix coefficients are based on the raw crossproduct matrix, whether a WEIGHT variable is specified or not.

NOCENTER

requests that the columns of the 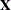$\mb{X}$ matrix are not centered and scaled. By default, the columns of 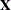$\mb{X}$ are centered and scaled. Unless the NOCENTER option is in effect, 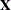$\mb{X}$ is replaced by 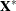$\mb{X}^*$ during estimation. The columns of 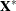$\mb{X}^*$ are computed as follows:

  • In models with an intercept, the intercept column remains the same and the jth entry in row i of 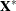$\mb{X}^*$ is

    \[ x^*_{ij} = \frac{x_{ij}-\overline{x}_ j}{\sqrt {\sum _{i=1}^{n}(x_{ij}-\overline{x}_ j)^2}} \]

  • In models without intercept, no centering takes place and the jth entry in row i of 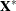$\mb{X}^*$ is

    \[ x^*_{ij} = \frac{x_{ij}}{\sqrt {\sum _{i=1}^{n}(x_{ij}-\overline{x}_ j)^2}} \]

The effects of centering and scaling are removed when results are reported. For example, if the covariance matrix of the fixed effects is printed with the COVB option of the MODEL statement, the covariances are reported in terms of the original parameters, not the centered and scaled versions. If you specify the STDCOEF option, fixed-effects parameter estimates and their standard errors are reported in terms of the standardized (scaled and/or centered) coefficients in addition to the usual results in noncentered form.

NOINT

requests that no intercept be included in the fixed-effects model. An intercept is included by default.

ODDSRATIO<(odds-ratio-options)>
OR<(odds-ratio-options)>

requests estimates of odds ratios and their confidence limits, provided the link function is the logit, cumulative logit, or generalized logit. Odds ratios are produced for the following:

  • classification main effects, if they appear in the MODEL statement

  • continuous variables in the MODEL statement, unless they appear in an interaction with a classification effect

  • continuous variables in the MODEL statement at fixed levels of a classification effect, if the MODEL statement contains an interaction of the two

  • continuous variables in the MODEL statement, if they interact with other continuous variables

You can specify the following odds-ratio-options to create customized odds ratio results.

AT var-list=value-list

specifies the reference values for continuous variables in the model. By default, the average value serves as the reference. Consider, for example, the following statements: 

proc glimmix;
   class A;
   model y = A x A*x / dist=binary oddsratio;
run;

Odds ratios for A are based on differences of least squares means for which x is set to its mean. Odds ratios for x are computed by differencing two sets of least squares mean for the A factor. One set is computed at x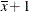 = $\overline{x}+1$, and the second set is computed at x = $\overline{x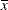}$. The following MODEL statement changes the reference value for x to 3: 

model y = A x A*x / dist=binary
                    oddsratio(at x=3);
DIFF<=difftype>

controls the type of differences for classification main effects. By default, odds ratios compare the odds of a response for level j of a factor to the odds of the response for the last level of that factor (DIFF=LAST). The DIFF=FIRST option compares the levels against the first level, DIFF=ALL produces odds ratios based on all pairwise differences, and DIFF=NONE suppresses odds ratios for classification main effects.

LABEL

displays a label in the "Odds Ratio Estimates" table. The table describes the comparison associated with the table row.

UNIT var-list=value-list

specifies the units in which the effects of continuous variable in the model are assessed. By default, odds ratios are computed for a change of one unit from the average. Consider a model with a classification factor A with 4 levels. The following statements produce an "Odds Ratio Estimates" table with 10 rows: 

proc glimmix;
   class A;
   model y = A x A*x / dist=binary
                       oddsratio(diff=all unit x=2);
run;

The first 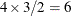$4 \times 3/2 = 6$ rows correspond to pairwise differences of levels of A. The underlying log odds ratios are computed as differences of A least squares means. In the least squares mean computation the covariate x is set to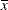 $\overline{x}$. The next four rows compare least squares means for A at x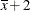 = $\overline{x}+2$ and at x = $\overline{x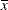}$. You can combine the AT and UNIT options to produce custom odds ratios. For example, the following statements produce an "Odds Ratio Estimates" table with 8 rows: 

proc glimmix;
   class A;
   model y = A x x*z / dist=binary
                       oddsratio(diff=all
                                 at   x   = 3
                                 unit x z = 2 4);
run;

The first 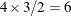$4 \times 3/2=6$ rows correspond to pairwise differences of levels of A. The underlying log odds ratios are computed as differences of A least squares means. In the least squares mean computation, the covariate x is set to 3, and the covariate x*z is set to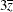 $3\overline{z}$. The next odds ratio measures the effect of a change in x. 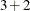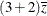It is based on differencing the linear predictor for x = $3+2$ and x*z = $(3+2)\overline{z}$ with the linear predictor for x = 3 and x*z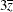 = $3\overline{z}$. The last odds ratio expresses a change in z by contrasting the linear predictors based on x = 3 and x*z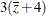 = $3(\overline{z}+4)$ with the predictor based on x = 3 and x*z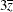 = $3\overline{z}$.

To compute odds and odds ratios for general estimable functions and least squares means, see the ODDSRATIO option in the LSMEANS statement and the EXP options in the ESTIMATE and LSMESTIMATE statements.

For important details concerning interpretation and computation of odds ratios with the GLIMMIX procedure, see the section Odds and Odds Ratio Estimation.

OFFSET=variable

specifies a variable to be used as an offset for the linear predictor. An offset plays the role of a fixed effect whose coefficient is known to be 1. You can use an offset in a Poisson model, for example, when counts have been obtained in time intervals of different lengths. With a log link function, you can model the counts as Poisson variables with the logarithm of the time interval as the offset variable. The offset variable cannot appear in the CLASS statement or elsewhere in the MODEL or RANDOM statement.

REFLINP=r

specifies a value for the linear predictor of the reference level in the generalized logit model for nominal data. By default r=0.

SOLUTION
S

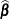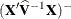requests that a solution for the fixed-effects parameters be produced. Using notation from the section Notation for the Generalized Linear Mixed Model, the fixed-effects parameter estimates are $\widehat{\bbeta }$, and their (approximate) estimated standard errors are the square roots of the diagonal elements of $\widehat{\mr{Var}}[\widehat{\bbeta }]$. This matrix commonly is of the form $(\mb{X}’\widehat{\mb{V}}^{-1}\mb{X})^-$ in GLMMs. You can output this approximate variance matrix with the COVB option. 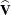See the section Details: GLIMMIX Procedure on the construction of $\widehat{\mb{V}}$ in the various models.

Along with the estimates and their approximate standard errors, a t statistic is computed as the estimate divided by its standard error. The degrees of freedom for this t statistic matches the one appearing in the "Type III Tests of Fixed Effects" table under the effect containing the parameter. If DDFM= KENWARDROGER or DDFM= SATTERTHWAITE, the degrees of freedom are computed separately for each fixed-effect estimate, unless you override the value for any specific effect with the DDF= value-list option. The "Pr > |t|" column contains the two-tailed p-value corresponding to the t statistic and associated degrees of freedom. You can use the CL option to request confidence intervals for the fixed-effects parameters; they are constructed around the estimate by using a radius of the standard error times a percentage point from the t distribution.

STDCOEF

reports solutions for fixed effects in terms of the standardized (scaled and/or centered) coefficients. This option has no effect when the NOCENTER option is specified or in models for multinomial data.

OBSWEIGHT<=variable>
OBSWT<=variable>

specifies a variable to be used as the weight for the observation-level unit in a weighted multilevel model. If a weight variable is not specified in the OBSWEIGHT option, a weight of 1 is used. For details on the use of weights in multilevel models, see the section Pseudo-likelihood Estimation for Weighted Multilevel Models.

ZETA=number

tunes the sensitivity in forming Type III functions. Any element in the estimable function basis with an absolute value less than number is set to 0. The default is 1E–8.