The GLIMMIX Procedure

OUTPUT Statement

OUTPUT <OUT=SAS-data-set>
<keyword<(keyword-options)> <=name>> …
<keyword<(keyword-options)> <=name>> </ options>;

The OUTPUT statement creates a data set that contains predicted values and residual diagnostics, computed after fitting the model. By default, all variables in the original data set are included in the output data set.

You can use the ID statement to select a subset of the variables from the input data set as well as computed variables for adding to the output data set. If you reassign a data set variable through programming statements, the value of the variable from the input data set supersedes the recomputed value when observations are written to the output data set. If you list the variable in the ID statement, however, PROC GLIMMIX saves the current value of the variable after the programming statements have been executed.

For example, suppose that data set Scores contains the variables score, machine, and person. The following statements fit a model with fixed machine and random person effects. The variable score divided by 100 is assumed to follow an inverse Gaussian distribution. The (conditional) mean and residuals are saved to the data set igausout. Because no ID statement is given, the variable score in the output data set contains the values from the input data set.

proc glimmix;
   class machine person;
   score = score/100;
   p = 4*_linp_;
   model score = machine  / dist=invgauss;
   random int / sub=person;
   output out=igausout pred=p resid=r;
run;

On the contrary, the following statements list explicitly which variables to save to the OUTPUT data set. Because the variable score is listed in the ID statement, and is (re-)assigned through programming statements, the values of score saved to the OUTPUT data set are the input values divided by 100.

proc glimmix;
   class machine person;
   score = score / 100;
   model score = machine  / dist=invgauss;
   random int / sub=person;
   output out=igausout pred=p resid=r;
   id machine score _xbeta_ _zgamma_;
run;

You can specify the following syntax elements in the OUTPUT statement before the slash (/).

OUT=SAS-data-set

specifies the name of the output data set. If the OUT= option is omitted, the procedure uses the DATAn convention to name the output data set.

keyword<(keyword-options)> <=name>

specifies a statistic to include in the output data set and optionally assigns the variable the name name. You can use the keyword-options to control which type of a particular statistic to compute. The keyword-options can take on the following values:

BLUP: uses the predictors of the random effects in computing the statistic.
ILINK: computes the statistic on the scale of the data.
NOBLUP: does not use the predictors of the random effects in computing the statistic.
NOILINK: computes the statistic on the scale of the link function.

The default is to compute statistics by using BLUPs on the scale of the link function (the linearized scale). For example, the following OUTPUT statements are equivalent:

output out=out1  pred=predicted lcl=lower;

output out=out1  pred(blup noilink)=predicted
                 lcl (blup noilink)=lower;

If a particular combination of keyword and keyword options is not supported, the statistic is not computed and a message is produced in the SAS log.

A keyword can appear multiple times in the OUTPUT statement. Table 44.15 lists the keywords and the default names assigned by the GLIMMIX procedure if you do not specify a name. In this table, y denotes the observed response, and p denotes the linearized pseudo-data. See the section Pseudo-likelihood Estimation Based on Linearization for details on notation and the section Notes on Output Statistics for further details regarding the output statistics.

Table 44.15: Keywords for Output Statistics

Keyword	Options	Description	Expression	Name
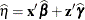
PREDICTED	Default	Linear predictor	$\widehat{\eta } = \mb{x}’\widehat{\bbeta }+\mb{z}’\widehat{\bgamma }$	Pred
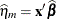
	NOBLUP	Marginal linear predictor	$\widehat{\eta }_ m = \mb{x}’\widehat{\bbeta }$	PredPA
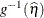
	ILINK	Predicted mean	$g^{-1}(\widehat{\eta })$	PredMu
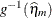
	NOBLUP ILINK	Marginal mean	$g^{-1}(\widehat{\eta }_ m)$	PredMuPA
STDERR	Default	Standard deviation of linear predictor	$\sqrt {\mr{Var}[\widehat{\eta }-\mb{z}’\bgamma ]}$	StdErr
	NOBLUP	Standard deviation of marginal linear predictor	$\sqrt {\mr{Var}[\widehat{\eta }_ m]}$	StdErrPA
	ILINK	Standard deviation of mean	$\sqrt {\mr{Var}[g^{-1}(\widehat{\eta }-\mb{z}’\bgamma )]}$	StdErr
	NOBLUP ILINK	Standard deviation of marginal mean	$\sqrt {\mr{Var}[g^{-1}(\widehat{\eta }_ m)]}$	StdErrMuPA
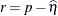
RESIDUAL	Default	Residual	$r = p - \widehat{\eta }$	Resid
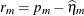
	NOBLUP	Marginal residual	$r_ m = p_ m - \widehat{\eta }_ m$	ResidPA
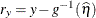
	ILINK	Residual on mean scale	$r_{y} = y - g^{-1}(\widehat{\eta })$	ResidMu
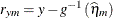
	NOBLUP ILINK	Marginal residual on mean scale	$r_{ym} = y - g^{-1}(\widehat{\eta }_ m)$	ResidMuPA
PEARSON	Default	Pearson-type residual	$r / \sqrt {\widehat{\mr{Var}}[p\|\bgamma ]}$	Pearson
	NOBLUP	Marginal Pearson-type residual	$r_ m / \sqrt {\widehat{\mr{Var}}[p_ m]}$	PearsonPA
	ILINK	Conditional Pearson-type mean residual	$r_ y / \sqrt {\widehat{\mr{Var}}[Y\|\bgamma ]}$	PearsonMu
STUDENT	Default	Studentized residual	$r / \sqrt {\widehat{\mr{Var}}[r]}$	Student
	NOBLUP	Studentized marginal residual	$r_ m / \sqrt {\widehat{\mr{Var}}[r_ m]}$	StudentPA
LCL	Default	Lower prediction limit for linear predictor		LCL
	NOBLUP	Lower confidence limit for marginal linear predictor		LCLPA
	ILINK	Lower prediction limit for mean		LCLMu
	NOBLUP ILINK	Lower confidence limit for marginal mean		LCLMuPA
UCL	Default	Upper prediction limit for linear predictor		UCL
	NOBLUP	Upper confidence limit for marginal linear predictor		UCLPA
	ILINK	Upper prediction limit for mean		UCLMu
	NOBLUP ILINK	Upper confidence limit for marginal mean		UCLMuPA
VARIANCE	Default	Conditional variance of pseudo-data	$\widehat{\mr{Var}}[p\|\bgamma ]$	Variance
	NOBLUP	Marginal variance of pseudo-data	$\widehat{\mr{Var}}[p_ m]$	VariancePA
	ILINK	Conditional variance of response	$\widehat{\mr{Var}}[Y\|\bgamma ]$	Variance_Dep
	NOBLUP ILINK	Marginal variance of response	$\widehat{\mr{Var}}[Y]$	Variance_DepPA

Studentized residuals are computed only on the linear scale (scale of the link), unless the link is the identity, in which case the two scales are equal. The keywords RESIDUAL, PEARSON, STUDENT, and VARIANCE are not available with the multinomial distribution. You can use the following shortcuts to request statistics: PRED for PREDICTED, STD for STDERR, RESID for RESIDUAL, and VAR for VARIANCE. Output statistics that depend on the marginal variance $\mr{Var}[Y_ i]$ are not available with METHOD= LAPLACE or METHOD= QUAD .

Table 44.16 summarizes the options available in the OUTPUT statement.

Table 44.16: OUTPUT Statement Options

Option	Description
ALLSTATS	Computes all statistics
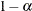ALPHA= $\alpha$	Determines the confidence level ( $1-\alpha$ )
CPSEUDO	Changes the way in which marginal residuals are computed
DERIVATIVES	Adds derivatives of model quantities to the output data set
NOMISS	Outputs only observations used in the analysis
NOUNIQUE	Requests that names not be made unique
NOVAR	Requests that variables from the input data set not be added to the output data set
OBSCAT	Writes statistics to output data set only for the response level corresponding to the observed level of the observation
SYMBOLS	Adds computed variables to the output data set

You can specify the following options in the OUTPUT statement after a slash (/).

ALLSTATS

requests that all statistics are computed. If you do not use a keyword to assign a name, the GLIMMIX procedure uses the default name.

ALPHA=number

determines the coverage probability for two-sided confidence and prediction intervals. The coverage probability is computed as 1 – number. The value of number must be between 0 and 1; the default is 0.05.

CPSEUDO

changes the way in which marginal residuals are computed when model parameters are estimated by pseudo-likelihood methods. See the section Notes on Output Statistics for details.

DERIVATIVES DER

adds derivatives of model quantities to the output data set. If, for example, the model fit requires the (conditional) log likelihood of the data, then the DERIVATIVES option writes for each observation the evaluations of the first and second derivatives of the log likelihood with respect to _LINP_ and _PHI_ to the output data set. The particular derivatives produced by the GLIMMIX procedure depend on the type of model and the estimation method.

NOMISS

requests that records be written to the output data only for those observations that were used in the analysis. By default, the GLIMMIX procedure produces output statistics for all observations in the input data set.

NOUNIQUE

requests that names not be made unique in the case of naming conflicts. By default, the GLIMMIX procedure avoids naming conflicts by assigning a unique name to each output variable. If you specify the NOUNIQUE option, variables with conflicting names are not renamed. In that case, the first variable added to the output data set takes precedence.

NOVAR

requests that variables from the input data set not be added to the output data set. This option does not apply to variables listed in the BY statement or to computed variables listed in the ID statement.

OBSCAT

requests that in models for multinomial data statistics be written to the output data set only for the response level that corresponds to the observed level of the observation.

SYMBOLS SYM

adds to the output data set computed variables that are defined or referenced in the program.