The Constraint Programming Solver (Experimental)

This example illustrates the use of the GCC constraint to find a feasible solution to a work-shift scheduling problem and then the use of the element constraint to incorporate cost information in order to find a minimum-cost schedule.

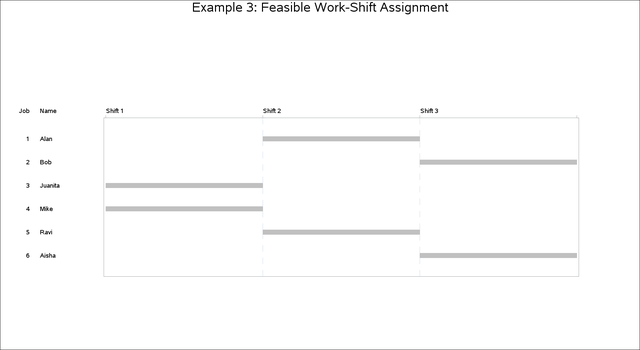
Six workers (Alan, Bob, Juanita, Mike, Ravi, and Aisha) are to be assigned to three working shifts. The first shift needs at least one and at most four people; the second shift needs at least two and at most three people; and the third shift needs exactly two people. Alan cannot work on the first shift; Bob can work only on the third shift. The others can work on any shift. The objective is to find a feasible assignment for this problem.

You can model the minimum and maximum shift requirements by using a GCC constraint and formulate the problem as a standard CSP. The variables W[1],,W[6] identify the shift to which each of the six workers is assigned: Alan, Bob, Juanita, Mike, Ravi, and Aisha.

proc optmodel;
   /*  Six workers (Alan, Bob, Juanita, Mike, Ravi and Aisha)
       are to be assigned to 3 working shifts.            */
   set WORKERS = 1..6;
   var W {WORKERS} integer >= 1 <= 3;

   /* The first shift needs at least 1 and at most 4 people;
      the second shift needs at least 2 and at most 3 people;
      and the third shift needs exactly 2 people. */
   con ShiftNeeds:
      gcc(W, /<1,1,4>,<2,2,3>,<3,2,2>/);

   /* Alan doesn't work on the first shift. */
   con Alan:
      W[1] ne 1;

   /* Bob works only on the third shift. */
   fix W[2] = 3;

   solve;
   print W;
quit;

The resulting assignment is shown in Output 6.3.1.

A Gantt chart of the corresponding schedule is displayed in Output 6.3.2.

Output 6.3.2: Work-Shift Schedule

Now suppose that every work-shift assignment has a cost associated with it and that the objective of interest is to determine the schedule that has the lowest cost.

The costs of assigning the workers to the different shifts are shown in Table 6.5. A dash ("-") in position indicates that worker i cannot work on shift j.

Based on the cost structure in Table 6.5, the previously derived schedule has a cost of $54. The objective now is to determine the optimal schedule—one that results in the minimum cost.

Let the variable represent the cost of assigning worker i to a shift. This variable is shift-dependent and is given a high value (for example, 100) if the worker cannot be assigned to a shift. The costs can also be interpreted as preferences if desired. You can use an element constraint to associate the cost with the shift assignment for each worker. For example, , the cost of assigning Alan to a shift, can be determined by the constraint ELEMENT().

By adding a linear constraint, , you can limit the solutions to feasible schedules that cost no more than obj. Although an upper bound of $100 is used in this example, it would suffice to use an upper bound of $54, the cost of the feasible schedule that was determined earlier.

proc optmodel;
   /* Six workers (Alan, Bob, Juanita, Mike, Ravi and Aisha)
      are to be assigned to 3 working shifts.  */
   set WORKERS = 1..6;
   set SHIFTS  = 1..3;
   var W {WORKERS} integer >= 1 <= 3;
   var C {WORKERS} integer >= 1 <= 100;

   /* The first shift needs at least 1 and at most 4 people;
      the second shift needs at least 2 and at most 3 people;
      and the third shift needs exactly 2 people. */
   con GccCon:
      gcc(W, /<1,1,4>,<2,2,3>,<3,2,2>/);

   /* Alan doesn't work on the first shift. */
   con Alan:
      W[1] ne 1;

   /* Bob works only on the third shift. */
   fix W[2] = 3;

   /* Specify the costs of assigning the workers to the shifts.
      Use 100 (a large number) to indicate an assignment
      that is not possible.*/
   num a {WORKERS, SHIFTS} = [
      100,  12, 10,
      100, 100,  6,
       16,   8, 12
       10,   6,  8
        6,   6,  8
       12,   4,  4
   ];
   con ElementCon {j in WORKERS}:
      element(W[j], {k in SHIFTS} a[j,k], C[j]);

   /* explicit objective instead of binary search */
   min TotalCost = sum {j in WORKERS} C[j];
   con TotalCost_bounds:
      1 <= TotalCost <= 100;

   solve;
   print W;
   create data clpout from
      {j in WORKERS} <col('W'||j)=W[j]> {j in WORKERS} <col('C'||j)=C[j]>;
quit;

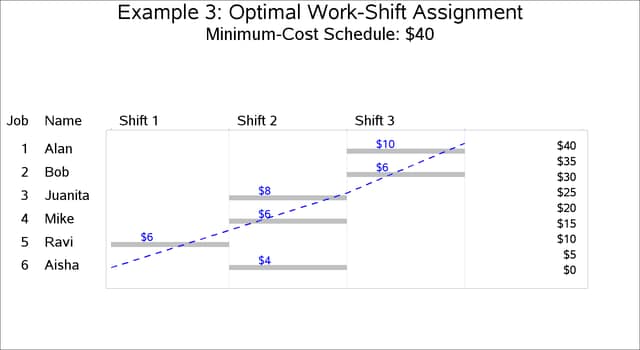
The cost of the optimal schedule, which corresponds to the solution shown in the following output, is $40.

The minimum-cost schedule is displayed in the Gantt chart in Output 6.3.3.

Output 6.3.3: Work-Shift Schedule with Minimum Cost