The Constraint Programming Solver (Experimental)
Balanced incomplete block design (BIBD) generation is a standard combinatorial problem from design theory. The concept was originally developed in the design of statistical experiments; applications have expanded to other fields, such as coding theory, network reliability, and cryptography. A BIBD is an arrangement of v distinct objects into b blocks such that the following conditions are met:
-
Each block contains exactly k distinct objects.
-
Each object occurs in exactly r different blocks.
-
Every two distinct objects occur together in exactly
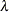 blocks.
blocks.
A BIBD is therefore specified by its parameters ![]() . It can be proved that when a BIBD exists, its parameters must satisfy the following conditions:
. It can be proved that when a BIBD exists, its parameters must satisfy the following conditions:
The preceding conditions are not sufficient to guarantee the existence of a BIBD (Prestwich, 2001). For example, the parameters ![]() satisfy the preceding conditions, but a BIBD that has these parameters does not exist. Computational methods of BIBD generation
usually suffer from combinatorial explosion, in part because of the large number of symmetries: for any solution, any two
objects or blocks can be exchanged to obtain another solution.
satisfy the preceding conditions, but a BIBD that has these parameters does not exist. Computational methods of BIBD generation
usually suffer from combinatorial explosion, in part because of the large number of symmetries: for any solution, any two
objects or blocks can be exchanged to obtain another solution.
This example demonstrates how to express a BIBD problem as a CSP and how to use lexicographic ordering constraints to break
symmetries. The most direct CSP model for BIBD, as described in Meseguer and Torras (2001), represents a BIBD as a ![]() matrix X. Each matrix entry is a Boolean decision variable
matrix X. Each matrix entry is a Boolean decision variable ![]() that satisfies
that satisfies ![]() if and only if block c contains object i. The condition that each object occurs in exactly r blocks (or, equivalently, that there are r 1s per row) can be expressed as v linear constraints:
if and only if block c contains object i. The condition that each object occurs in exactly r blocks (or, equivalently, that there are r 1s per row) can be expressed as v linear constraints:
Alternatively, you can use global cardinality constraints to ensure that there are exactly ![]() 0s and r 1s in
0s and r 1s in ![]() , …,
, …, ![]() for each object i:
for each object i:
Similarly, you can use the following constraints to specify the condition that each block contain exactly k objects (there are k 1s per column):
To enforce the final condition that every two distinct objects occur together in exactly ![]() blocks (equivalently, that the scalar product of every pair of rows equal
blocks (equivalently, that the scalar product of every pair of rows equal ![]() ), you can introduce the auxiliary variables
), you can introduce the auxiliary variables ![]() for every
for every ![]() , which indicate whether objects i and j both occur in block c. The following reify constraint ensures that
, which indicate whether objects i and j both occur in block c. The following reify constraint ensures that ![]() if and only if block c contains both objects i and j:
if and only if block c contains both objects i and j:
The following constraints ensure that the final condition holds:
The objects and the blocks are interchangeable, so the matrix X has total row symmetry and total column symmetry. Because of the constraints on the rows, no pair of rows can be equal unless
![]() . To break the row symmetry, you can impose strict lexicographic ordering on the rows of X as follows:
. To break the row symmetry, you can impose strict lexicographic ordering on the rows of X as follows:
To break the column symmetry, you can impose lexicographic ordering on the columns of X as follows:
The following SAS macro incorporates all the preceding constraints. For the specified parameters ![]() , the macro either finds BIBDs or proves that a BIBD does not exist.
, the macro either finds BIBDs or proves that a BIBD does not exist.
%macro bibd(v, b, r, k, lambda, out=bibdout);
/* Arrange v objects into b blocks such that:
(i) each object occurs in exactly r blocks,
(ii) each block contains exactly k objects,
(iii) every pair of objects occur together in exactly lambda blocks.
Equivalently, create a binary matrix with v rows and b columns,
with r 1s per row, k 1s per column,
and scalar product lambda between any pair of distinct rows.
*/
/* Check necessary conditions */
%if (%eval(&r * &v) ne %eval(&b * &k)) or
(%eval(&lambda * (&v - 1)) ne %eval(&r * (&k - 1))) or
(&v > &b) %then %do;
%put BIBD necessary conditions are not met.;
%goto EXIT;
%end;
proc optmodel;
num v = &v;
num b = &b;
num r = &r;
num k = &k;
num lambda = λ
set OBJECTS = 1..v;
set BLOCKS = 1..b;
/* Decision variable X[i,c] = 1 iff object i occurs in block c. */
var X {OBJECTS, BLOCKS} binary;
/* Mandatory constraints: */
/* (i) Each object occurs in exactly r blocks. */
con Exactly_r_blocks {i in OBJECTS}:
gcc({c in BLOCKS} X[i,c], {<0,0,b-r>,<1,0,r>});
/* (ii) Each block contains exactly k objects. */
con Exactly_k_objects {c in BLOCKS}:
gcc({i in OBJECTS} X[i,c], {<0,0,v-k>,<1,0,k>});
/* (iii) Every pair of objects occurs in exactly lambda blocks. */
set PAIRS = {i in OBJECTS, j in OBJECTS: i < j};
/* auxiliary variable P[i,j,c] = 1 iff both i and j occur in c */
var P {PAIRS, BLOCKS} binary;
con Pairs_reify {<i,j> in PAIRS, c in BLOCKS}:
reify(P[i,j,c], X[i,c] + X[j,c] = 2);
con Pairs_gcc {<i,j> in PAIRS}:
gcc({c in BLOCKS} P[i,j,c], {<0,0,b-lambda>,<1,0,lambda>});
/* symmetry-breaking constraints: */
/* Break row symmetry via lexicographic ordering constraints. */
con Symmetry_i {i in OBJECTS diff {1}}:
lexico({c in BLOCKS} X[i,c] < {c in BLOCKS} X[i-1,c]);
/* Break column symmetry via lexicographic ordering constraints. */
con Symmetry_c {c in BLOCKS diff {1}}:
lexico({i in OBJECTS} X[i,c] <= {i in OBJECTS} X[i,c-1]);
solve with CLP / varselect=FIFO;
create data &out from
{i in OBJECTS, c in BLOCKS} <col('X'||i||'_'||c)=X[i,c]>;
quit;
%put &_oroptmodel_;
%EXIT:
%mend bibd;
The following statement invokes the macro to find a BIBD design for the parameters ![]() :
:
%bibd(15,15,7,7,3);
The output is displayed in Output 6.8.1.
Output 6.8.1: Balanced Incomplete Block Design for (15,15,7,7,3)
| Balanced Incomplete Block Design Problem |
| (15, 15, 7, 7, 3) |
| Obs | Block1 | Block2 | Block3 | Block4 | Block5 | Block6 | Block7 | Block8 | Block9 | Block10 | Block11 | Block12 | Block13 | Block14 | Block15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 4 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 5 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 |
| 6 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 7 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 8 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 9 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 10 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 11 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 12 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 13 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 14 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 15 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
