The Constraint Programming Solver (Experimental)

Overview: CLP Solver

You can use the constraint logic programming (CLP) solver in the OPTMODEL procedure to address finite-domain constraint satisfaction problems (CSPs) that have linear, logical, and global constraints. In addition to providing an expressive syntax for representing CSPs, the CLP solver features powerful built-in consistency routines and constraint propagation algorithms, a choice of nondeterministic search strategies, and controls for guiding the search mechanism. These features enable you to solve a diverse array of combinatorial problems.

Many important problems in areas such as artificial intelligence (AI) and operations research (OR) can be formulated as constraint satisfaction problems. A CSP is defined by a finite set of variables that take values from finite domains and by a finite set of constraints that restrict the values that the variables can simultaneously take.

A solution to a CSP is an assignment of values to the variables in order to satisfy all the constraints. The problem amounts to finding one or more solutions, or possibly determining that a solution does not exist.

A constraint satisfaction problem (CSP) can be defined as a triplet $\langle X, D, C \rangle $:

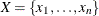  • $ X = \{ x_1,\ldots , x_ n\} $ is a finite set of variables.

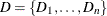  • $ D = \{ D_1,\ldots , D_ n\} $ is a finite set of domains, where a domain 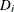$ D_ i$ is a finite set of possible values that the variable 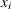$ x_ i$ can take. 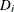$ D_ i$ is known as the domain of variable $ x_ i$.

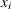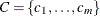  • $ C = \{ c_1, \ldots , c_ m\} $ is a finite set of constraints that restrict the values that the variables can simultaneously take.

The domains do not need to represent consecutive integers. For example, the domain of a variable could be the set of all even numbers in the interval [0, 100]. In PROC OPTMODEL, variables are always numeric. Therefore, if your problem contains nonnumeric domains (such as colors), you must map the values in the domain to integers. For more information, see Example 6.5 Car Painting Problem.

You can use the CLP solver to find one or more (and in some instances, all) solutions to a CSP that has linear, logical, and global constraints. The numeric components of all variable domains are required to be integers.