The Constraint Programming Solver (Experimental)

Example 6.5 Car Painting Problem

The car painting process is an important part of the automobile manufacturing industry. Purging (the act of changing colors during assembly) is expensive because of the added cost of wasted paint and solvents from each color change and the extra time that the purging process requires. The objective of the car painting problem is to sequence the cars in the assembly line in order to minimize the number of paint color changes (Sokol, 2002; Trick, 2004).

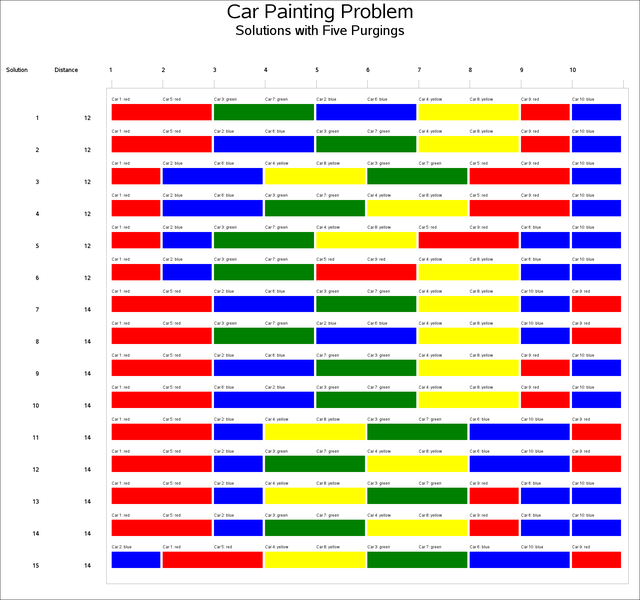
Suppose an assempbly line contains 10 cars, which are ordered 1, 2, …, 10. A car must be painted within three positions of its assembly order. For example, car 5 can be painted in positions 2 through 8. Cars 1, 5, and 9 are red; 2, 6, and 10 are blue; 3 and 7 green; and 4 and 8 are yellow. The initial sequence 1, 2, …, 10 corresponds to the color pattern RBGYRBGYRB and has nine purgings. The objective is to find a solution that minimizes the number of purgings.

This problem can be formulated as a CSP as follows:

  • The input is the color of each car currently on the assembly line.

  • The output variables are the slot in which each car will be painted and whether purging will be required after that painting operation.

  • Set the bounds of the slot variables to their feasible range, at most three slots before or after the car’s current position.

  • To determine whether purging is needed, use another variable to store the color of the car painted in each slot.

  • Use an element constraint to determine the color used in each slot from the car assigned to that slot.

  • Use a reify constraint to determine whether two consecutive slots are assigned different colors, and thus whether purging is required.

  • Finally, use a linear constraint to limit the total number of purgings.

The following %CAR_PAINTING macro determines all feasible solutions for the number of purgings that is specified as a parameter to the macro: 

%macro car_painting(purgings);
   proc optmodel;
      num nCars = 10;
      /* a car is identified by its original slots */
      set SLOTS = 1..nCars;

      /* maximum reshuffling of any car on the line*/
      num maxMove init 3;
      /* which car is in slot i. */
      var S {si in SLOTS} integer >= max(1, si - maxMove)
                                  <= min(nCars, si + maxMove) ;

      /* which color the car in slot i is. */
      /* Red=1; Blue=2; Green=3; Yellow=4 */
      num nColors=4;
      num colorOf{SLOTS} = [ 1 2 3 4 1 2 3 4 1 2 ];
      var C {SLOTS} integer >= 1 <= nColors;

      con ElementCon {i in SLOTS}:
         element(S[i], colorOf, C[i]);

      /* A car can be painted only once. */
      con PaintOnlyOnce:
         alldiff(S);

      /* Whether there is a purge after slot i.
        You can ignore any purging that would happen at the end of the shift. */
      var P {SLOTS diff {nCars}} binary;

      con ReifyCon {i in SLOTS diff {nCars}}:
         reify(P[i], C[i] ne C[i+1]);

      /* Calculate the number of purgings. */
      con PurgingsCon:
         sum {i in SLOTS diff {nCars}} P[i] <= &purgings;

      solve with CLP / findall;
      /* Replicate typical PROC CLP output from PROC OPTMODEL arrays */
      create data car_ds(drop=k) from [k]=(1.._NSOL_)
         {i in SLOTS} <col('S'||i)=S[i].sol[k]>
         {i in SLOTS} <col('C'||i)=C[i].sol[k]>;
   quit;
%mend;
%car_painting(5);

The problem is infeasible for four purgings. The CLP solver finds 87 possible solutions for the five-purgings problem. The solutions are sorted by the total distance that all cars are moved in the sequencing, which ranges from 12 to 22 slots. The first 15 solutions are displayed in the Gantt chart in Output 6.5.1. Each row represents a solution, and each color transition represents a paint purging.

Output 6.5.1: Car Painting Schedule with Five Purgings

Car Painting Schedule with Five Purgings