The Constraint Programming Solver (Experimental)
This example demonstrates the use of the pack constraint to solve an instance of the progressive party problem (Smith et al., 1996). In the original progressive party problem, a number of yacht crews and their boats congregate at a yachting rally. In order for each crew to socialize with as many other crews as possible, some of the boats are selected to serve as "host boats" for six rounds of parties. The crews of the host boats stay with their boats for all six rounds. The crews of the remaining boats, called "guest crews," are assigned to visit a different host boat in each round.
Given the number of boats at the rally, the capacity of each boat, and the size of each crew, the objective of the original problem is to assign all the guest crews to host boats for each of the six rounds, using the minimum number of host boats. The partitioning of crews into guests and hosts is fixed throughout all rounds. No two crews should meet more than once. The assignments are constrained by the spare capacities (total capacity minus crew size) of the host boats and the crew sizes of the guest boats. Some boats cannot be hosts (zero spare capacity), and other boats must be hosts.
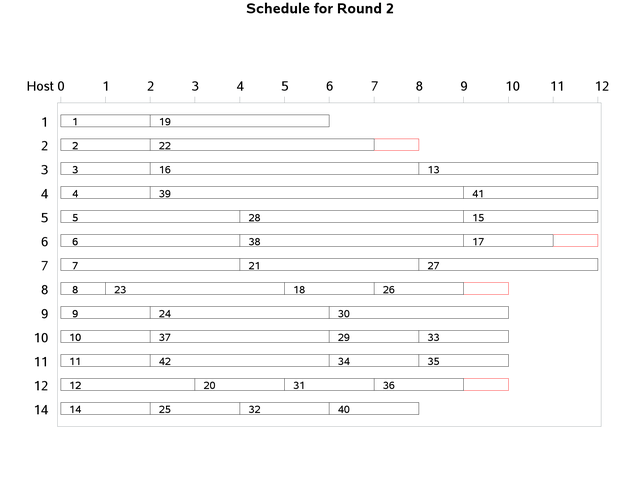
In this instance of the problem, the designation of the minimum requirement of 13 hosts is assumed (boats 1 through 12 and 14). The formulation solves up to eight rounds, but only two rounds are scheduled for this example. The total capacities and crew sizes of the boats are shown in Output 6.9.1.
Output 6.9.1: Progressive Party Problem Input
| Progressive Party Problem Input |
| boatnum | capacity | crewsize |
|---|---|---|
| 1 | 6 | 2 |
| 2 | 8 | 2 |
| 3 | 12 | 2 |
| 4 | 12 | 2 |
| 5 | 12 | 4 |
| 6 | 12 | 4 |
| 7 | 12 | 4 |
| 8 | 10 | 1 |
| 9 | 10 | 2 |
| 10 | 10 | 2 |
| 11 | 10 | 2 |
| 12 | 10 | 3 |
| 13 | 8 | 4 |
| 14 | 8 | 2 |
| 15 | 8 | 3 |
| 16 | 12 | 6 |
| 17 | 8 | 2 |
| 18 | 8 | 2 |
| 19 | 8 | 4 |
| 20 | 8 | 2 |
| 21 | 8 | 4 |
| 22 | 8 | 5 |
| 23 | 7 | 4 |
| 24 | 7 | 4 |
| 25 | 7 | 2 |
| 26 | 7 | 2 |
| 27 | 7 | 4 |
| 28 | 7 | 5 |
| 29 | 6 | 2 |
| 30 | 6 | 4 |
| 31 | 6 | 2 |
| 32 | 6 | 2 |
| 33 | 6 | 2 |
| 34 | 6 | 2 |
| 35 | 6 | 2 |
| 36 | 6 | 2 |
| 37 | 6 | 4 |
| 38 | 6 | 5 |
| 39 | 9 | 7 |
| 40 | 0 | 2 |
| 41 | 0 | 3 |
| 42 | 0 | 4 |
The following statements and DATA steps process the data and designate host boats:
data hostability;
set capacities;
spareCapacity = capacity - crewsize;
run;
data hosts guests;
set hostability;
if (boatnum <= 12 or boatnum eq 14) then do;
output hosts;
end;
else do;
output guests;
end;
run;
/* sort so guest boats with larger crews appear first */
proc sort data=guests;
by descending crewsize;
run;
data capacities;
format boatnum capacity 2.;
set hosts guests;
seqno = _n_;
run;
To model the progressive party problem for the CLP solver, first define the following sets of variables:
-
Item variables
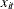 contain the host boat number for the assignment of guest boat i in round t.
contain the host boat number for the assignment of guest boat i in round t.
-
Load variables
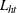 contain the load of host boat h in round t.
contain the load of host boat h in round t.
-
Variable
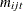 are binary variables that take a value of 1 if and only if guest boats i and j are assigned to the same host boat in round t.
are binary variables that take a value of 1 if and only if guest boats i and j are assigned to the same host boat in round t.
Next, describe the set of constraints that are used in the model:
-
All-different constraints ensure that a guest boat is not assigned to the same host boat in different rounds.
-
Reify constraints regulate the values that are assigned to the aforementioned indicator variables
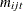 .
.
-
The reified indicator variables appear in linear constraints to enforce the requirement to meet no more than once.
-
One pack constraint per round maintains the capacity limits of the host boats.
-
Finally, a symmetry-breaking linear constraint orders the host boat assignments for the highest-numbered guest boat across rounds.
The following statements call PROC OPTMODEL to define the variables, specify the constraints, and solve the problem:
%let rounds=2;
%let numhosts=13;
proc optmodel;
num numrounds = &rounds;
set ROUNDS = 1..numrounds;
num numhosts = &numhosts;
set HOSTS = 1..numhosts;
set BOATS;
num numboats = card(BOATS);
num capacity {BOATS};
num crewsize {BOATS};
num spareCapacity{hi in HOSTS} = capacity[hi] - crewsize[hi];
/* Use the descending crew order for guests (seqno)
rather than the actual boat id (boatnum)
to help the performance of the PACK predicate. */
read data capacities into BOATS=[seqno] capacity crewsize;
/* Assume that the first numhosts boats are hosts,
and process each round in turn.
X is the host assigned to non-host i for round t. */
var X {numhosts+1..numboats, ROUNDS} integer >= 1 <= numhosts;
/* The load of the host boat. */
var L {hi in HOSTS, ROUNDS} integer >= 0 <= spareCapacity[hi];
/* Assign different hosts each round. */
con AlldiffCon {i in numhosts+1..numboats}:
alldiff({t in ROUNDS} X[i,t]);
/* Don't assign two non-hosts to the same host in round t. */
var M {i in numhosts+1..numboats-1, j in i+1..numboats, t in ROUNDS} binary;
con ReifyCon {i in numhosts+1..numboats-1, j in i+1..numboats, t in ROUNDS}:
reify(M[i,j,t], X[i,t] = X[j,t]);
con Assign {i in numhosts+1..numboats-1, j in i+1..numboats}:
sum {t in ROUNDS} M[i,j,t] <= 1;
/* Honor capacities. */
con PackCon {t in ROUNDS}:
pack(
{i in numhosts+1..numboats} X[i,t],
{i in numhosts+1..numboats} crewsize[i],
{h in HOSTS} L[h,t]
);
/* Break symmetries. */
con SymmetryCon {t in 1..numrounds-1}:
X[numboats,t] < X[numboats,t+1];
solve with CLP / varselect=FIFO;
quit;
The two charts in Output 6.9.2 show the boat assignments for the first two rounds. The horizontal axis shows the load for each host boat. Slack capacity is highlighted in red.
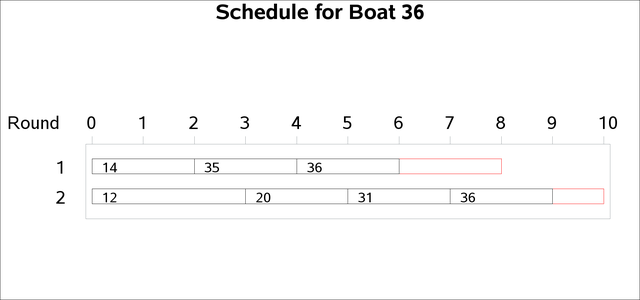
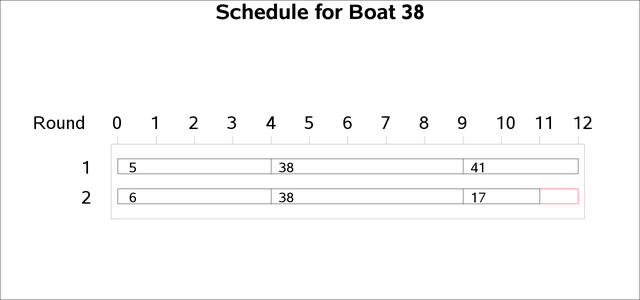
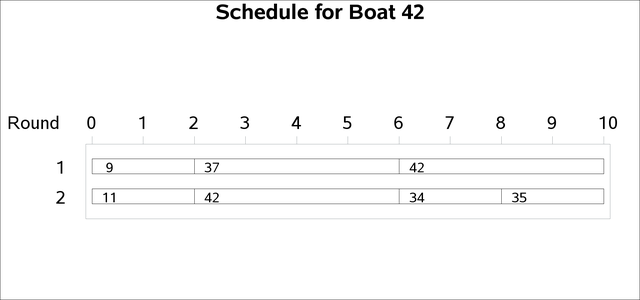
The charts in Output 6.9.3 break down the assignments by boat number for selected boats.