The Constraint Programming Solver (Experimental)

Example 6.4 A Nonlinear Optimization Problem

This example illustrates how you can use the element constraint to represent almost any function between two variables in addition to representing nonstandard domains. Consider the following nonlinear optimization problem:

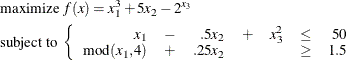
\begin{align*} & \mbox{maximize } f(x)= x_1^3 + 5x_2 - 2^{x_3} & \\ & \mbox{subject to } \left\{ \begin{array}{rrrrrrrr} x_1 & - & .5x_2 & +& x_3^2 & \le & 50 \\ \mbox{mod}(x_1, 4)& +& .25 x_2 & & & \ge & 1.5 \end{array} \right. \end{align*}

where $x_1$ is any integer in [–5, 5], $x_2$ is any odd integer in [–5, 9], and $x_3$ is any integer in [1, 10].

You can solve this problem by introducing four artificial variables, $y_1$–$y_4$, to represent each of the nonlinear terms. Let $y_1=x_1^3$, $y_2=2^{x_3}$, $y_3= x_3^2 $, and $y_4=\mbox{mod}(x_1, 4)$. You can represent the domains of $x_1$ and $x_2$ (which are not consecutive integers that start from 1) by using element constraints and index variables. For example, any of the following three element constraints specifies that the domain of $x_2$ is the set of odd integers in $[-5,9]$: 

con element(z2,-5 -3 -1 1 3 5 7 9,x2);
con element(z2, {ri in -5..9 by 2} ri, x2);
num range{ri in -5..9 by 2} = ri;
con element(z2,range,x2);

Any functional dependencies on $x_1$ or $x_2$ can now be defined using $z_1$ or $z_2$, respectively, as the index variable in an element constraint. Because the domain of $x_3$ is $[1,10]$, you can directly use $x_3$ as the index variable in an element constraint to define dependencies on $x_3$.

For example, the following constraint specifies the function $y_1=x_1^3$, $x_1 \in [-5,5]$: 

con element(z1,-125 -64 -27 -8 -1 0 1 8 27 64 125,y1);
/* or, con element(z1, {ri in -5..5} (ri**3), y1}; */
num range{ri in -5..5} = ri**3;
con element(z1,range,y1);

To solve the problem, define the objective function as demonstrated in the following statements: 

proc optmodel;
   set DOM{1..3} = [ (-5 .. 5) (-5 .. 9 by 2) (1 .. 10) ];
   var X{i in 1..3} integer >= min{j in DOM[i]} j <= max{j in DOM[i]} j;

   /* map the domain of X[1] and X[2] to 1 .. list size */
   var Z {1..2} integer;
   /* map nonlinear expressions */
   var Y {1..4} integer;

   /* Use an element constraint to represent noncontiguous domains */
   /* domains with negative numbers, and nonlinear functions. */
   /* Z[2] does not appear anywhere else. Its only purpose is
      to restrict X[2] to take a value from DOM[2]. */
   con MapDomainTo1ToCard{i in 1..2}:
      element(Z[i], {k in DOM[i]} k, X[i]);

   /* Functional Dependencies on X[1] */
   /* Y[1] = X[1]^3 -- Use Z[1] for X[1] for proper indexing */
   con Y1:
      element(Z[1], {k in DOM[1]} (k^3), Y[1]);

   /* Y[4] = mod(X[1], 4) */
   con Y4:
      element(Z[1], {k in DOM[1]} (mod(k,4)), Y[4]);


   /* Functional Dependencies on X[3] */
   /* Y[2] = 2^X[3] */
   con Y2:
      element(X[3], {k in DOM[3]} (2^k), Y[2]);

   /* Y[3] = X[3]^2 */
   con Y3:
      element(X[3], {k in DOM[3]} (k^2), Y[3]);

   /* X[1] - 0.5 * X[2] + X[3]^2 <= 50 */
   con Con1:
      X[1] - 0.5 * X[2] + Y[3] <= 50;

   /* mod(X[1],4) + 0.25 * X[2] >= 1.5 */
   con Con2:
      Y[4] + 0.25 * X[2] >= 1.5;

   /* Objective function: X[1]^3 + 5 * X[2] - 2^X[3] */
   max Objective = Y[1] + 5 * X[2] - Y[2];

   solve;
   print X Y Z;
quit;

Output 6.4.1 shows the solution that corresponds to the optimal objective value of 168.

Output 6.4.1: Nonlinear Optimization Problem Solution

The OPTMODEL Procedure

Problem Summary
Objective Sense Maximization
Objective Function Objective
Objective Type Linear
   
Number of Variables 9
Bounded Above 0
Bounded Below 0
Bounded Below and Above 3
Free 6
Fixed 0
Binary 0
Integer 9
   
Number of Constraints 8
Linear LE (<=) 1
Linear EQ (=) 0
Linear GE (>=) 1
Linear Range 0
Alldiff 0
Element 6
GCC 0
Lexico (<=) 0
Lexico (<) 0
Pack 0
Reify 0
   
Constraint Coefficients 5

Performance Information
Execution Mode Single-Machine
Number of Threads 1

Solution Summary
Solver CLP
Objective Function Objective
Solution Status Optimal
Objective Value 168
   
Solutions Found 1
Presolve Time 0.00
Solution Time 0.00

[1] X Y Z
1 5 125 11
2 9 2 8
3 1 1  
4   1