The Network Solver

Minimum Cut

Subsections:

Minimum Cut for a Simple Undirected Graph

A cut is a partition of the nodes of a graph into two disjoint subsets. The cut-set is the set of links whose from and to nodes are in different subsets of the partition. A minimum cut of an undirected graph is a cut whose cut-set has the smallest link metric, which is measured as follows: For an unweighted graph, the link metric is the number of links in the cut-set. For a weighted graph, the link metric is the sum of the link weights in the cut-set.

In the network solver, you can invoke the minimum cut algorithm by using the MINCUT= option. This algorithm can be used only on undirected graphs.

If the value of the MAXNUMCUTS= suboption is greater than 1, then the algorithm can return more than one set of cuts. The resulting cuts can be described in terms of partitions of the nodes of the graph or the links in the cut-sets. The example in the next section illustrates several ways to manipulate the output from the minimum cut algorithm. The node partition is specified in the PARTITIONS= suboption of the OUT= option in the SOLVE WITH NETWORK statement. Each tuple in this set has a cut ID and a node. PROC OPTMODEL provides only the smaller of the two subsets that form each partition. Use the DIFF set operator to get the complement of each partition. The cut-set is specified in the CUTSETS= suboption of the OUT= option. This set contains the cut ID and the corresponding list of links.

The network solver uses the Stoer-Wagner algorithm (Stoer and Wagner 1997) to compute the minimum cuts. This algorithm runs in time $O(|N||A| + |N|^2 \log |N|)$ .

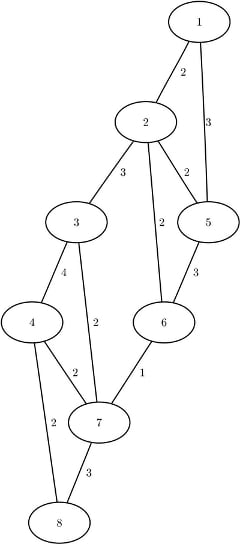
Minimum Cut for a Simple Undirected Graph

As a simple example, consider the weighted undirected graph in Figure 9.45.

Figure 9.45: A Simple Undirected Graph

The links data set can be represented as follows:

data LinkSetIn;
   input from to weight @@;
   datalines;
1 2 2  1 5 3  2 3 3  2 5 2  2 6 2
3 4 4  3 7 2  4 7 2  4 8 2  5 6 3
6 7 1  7 8 3
;

The following statements calculate minimum cuts in the graph and output the results in the data set MinCut:

proc optmodel;
   set<num,num> LINKS;
   num weight{LINKS};
   read data LinkSetIn into LINKS=[from to] weight;
   set<num> NODES = union {<i,j> in LINKS} {i,j};
   set<num,num> PARTITIONS;
   set<num,num,num> CUTSETS;

   solve with NETWORK /
      loglevel = moderate
      links    = (weight=weight)
      mincut   = (maxnumcuts=3)
      out      = (partitions=PARTITIONS cutsets=CUTSETS)
   ;
   set CUTS = setof {<cut,i,j> in CUTSETS} cut;
   num minCutWeight {cut in CUTS} = sum {<(cut),i,j> in CUTSETS} weight[i,j];
   print minCutWeight;

   for { cut in CUTS }
      put "Cut ID: "    cut
          "Partition: " ( slice( <cut,*>, PARTITIONS ) )
          "and "        ( NODES diff slice( <cut,*>, PARTITIONS ) )
          "Cut: "       ( slice( <cut,*,*>, CUTSETS ) )
          "Weight: "    minCutWeight[cut];

   create data MinCut from [mincut from to]=CUTSETS weight[from,to];
   num mincut {cut in CUTS, node in NODES} =
      if <cut,node> in PARTITIONS then 0 else 1;
   print mincut;
   create data NodeSetOut from [node]=NODES
      {cut in CUTS} <col('mincut_'||cut)=mincut[cut,node]>;
quit;

The progress of the procedure is shown in Figure 9.46.

Figure 9.46: Network Solver Log for Minimum Cut

NOTE: There were 12 observations read from the data set WORK.LINKSETIN.

NOTE: The number of nodes in the input graph is 8.

NOTE: The number of links in the input graph is 12.

NOTE: Processing the minimum-cut problem.

NOTE: The minimum-cut algorithm found 3 cuts.

NOTE: The cut 1 has weight 4.

NOTE: The cut 2 has weight 5.

NOTE: The cut 3 has weight 5.

NOTE: Processing the minimum-cut problem used 0.00 (cpu: 0.00) seconds.

Cut ID: 1 Partition: {3,4,7,8} and {1,2,5,6} Cut: {<2,3>,<6,7>} Weight: 4

Cut ID: 2 Partition: {8} and {1,2,5,3,6,4,7} Cut: {<4,8>,<7,8>} Weight: 5

Cut ID: 3 Partition: {1} and {2,5,3,6,4,7,8} Cut: {<1,2>,<1,5>} Weight: 5

NOTE: The data set WORK.MINCUT has 6 observations and 4 variables.

NOTE: The data set WORK.NODESETOUT has 8 observations and 4 variables.

The data set NodeSetOut now contains the partition of the nodes for each cut, shown in Figure 9.47.

Figure 9.47: Minimum Cut Node Partition

node	mincut_1	mincut_2	mincut_3
1	1	1	0
2	1	1	1
5	1	1	1
3	0	1	1
6	1	1	1
4	0	1	1
7	0	1	1
8	0	0	1

The data set MinCut contains the links in the cut-sets for each cut. This data set is shown in Figure 9.48, which also shows each cut separately.

Figure 9.48: Minimum Cut-sets

mincut	from	to	weight
1	2	3	3
1	6	7	1
2	4	8	2
2	7	8	3
3	1	2	2
3	1	5	3

mincut=1

from	to	weight
2	3	3
6	7	1
mincut		4

mincut=2

from	to	weight
4	8	2
7	8	3
mincut		5

mincut=3

from	to	weight
1	2	2
1	5	3
mincut		5
		14