The Network Solver

This section shows an introductory example for getting started with the network solver. For more information about the expected input formats and the various algorithms available, see the sections Details: Network Solver and Examples: Network Solver.

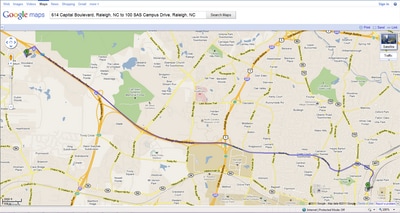
Consider the following road network between a SAS employee’s home in Raleigh, NC, and the SAS headquarters in Cary, NC.

In this road network (graph), the links are the roads and the nodes are intersections between roads. For each road, you assign a link attribute in the variable time_to_travel to describe the number of minutes that it takes to drive from one node to another. The following data were collected using Google Maps (Google 2011):

data LinkSetInRoadNC10am;
   input start_inter $1-20 end_inter $20-40 miles miles_per_hour;
   datalines;
614CapitalBlvd      Capital/WadeAve      0.6  25
614CapitalBlvd      Capital/US70W        0.6  25
614CapitalBlvd      Capital/US440W       3.0  45
Capital/WadeAve     WadeAve/RaleighExpy  3.0  40
Capital/US70W       US70W/US440W         3.2  60
US70W/US440W        US440W/RaleighExpy   2.7  60
Capital/US440W      US440W/RaleighExpy   6.7  60
US440W/RaleighExpy  RaleighExpy/US40W    3.0  60
WadeAve/RaleighExpy RaleighExpy/US40W    3.0  60
RaleighExpy/US40W   US40W/HarrisonAve    1.3  55
US40W/HarrisonAve   SASCampusDrive       0.5  25
;

Using the network solver, you want to find the route that yields the shortest path between home (614 Capital Blvd) and the SAS headquarters (SAS Campus Drive). This can be done by using the SHORTPATH= option as follows:

proc optmodel;
   set<str,str> LINKS;
   num miles{LINKS};
   num miles_per_hour{LINKS};
   num time_to_travel{<i,j> in LINKS} = miles[i,j]/ miles_per_hour[i,j] * 60;
   read data LinkSetInRoadNC10am into
      LINKS=[start_inter end_inter]
      miles miles_per_hour
   ;
   /* You can compute paths between many pairs of source and destination,
      so these parameters are declared as sets */
   set HOME = /"614CapitalBlvd"/;
   set WORK = /"SASCampusDrive"/;

   /* The path is stored as a set of: Start, End, Sequence, Tail, Head */
   set<str,str,num,str,str> PATH;

   solve with network /
      links     = ( weight = time_to_travel )
      shortpath = ( source = HOME
                    sink   = WORK )
      out       = ( sppaths = PATH )
   ;
   create data ShortPath from [s t order start_inter end_inter]=PATH
      time_to_travel[start_inter,end_inter];
quit;

For more information about shortest path algorithms in the network solver, see the section Shortest Path. Figure 9.1 displays the output data set ShortPath, which shows the best route to take to minimize travel time at 10:00 a.m. This route is also shown in Google Maps in Figure 9.2.

Figure 9.2: Shortest Path for Road Network at 10:00 A.M. in Google Maps

Now suppose that it is rush hour (5:00 p.m.) and the time to traverse the roads has changed because of traffic patterns. You want to find the route that is the shortest path for going home from SAS headquarters under different speed assumptions due to traffic.

The following statements are similar to the first network solver run, except that one miles_per_hour value is modified and the SOURCE= and SINK= option values are reversed:

proc optmodel;
   set<str,str> LINKS;
   num miles{LINKS};
   num miles_per_hour{LINKS};
   num time_to_travel{<i,j> in LINKS} = miles[i,j]/ miles_per_hour[i,j] * 60;
   read data LinkSetInRoadNC10am into
      LINKS=[start_inter end_inter]
      miles miles_per_hour
   ;
   /* high traffic */
   miles_per_hour['Capital/WadeAve','WadeAve/RaleighExpy'] = 25;

   /* You can compute paths between many pairs of source and destination,
      so these parameters are declared as sets */
   set HOME = /"614CapitalBlvd"/;
   set WORK = /"SASCampusDrive"/;

   /* The path is stored as a set of: Start, End, Sequence, Tail, Head */
   set<str,str,num,str,str> PATH;

   solve with network /
      links     = ( weight = time_to_travel )
      shortpath = ( source = WORK
                    sink   = HOME )
      out       = ( sppaths = PATH )
   ;
   create data ShortPath from [s t order start_inter end_inter]=PATH
      time_to_travel[start_inter,end_inter];
quit;

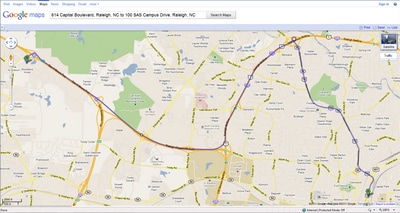
Now, the output data set ShortPath, shown in Figure 9.3, shows the best route for going home at 5:00 p.m. Because the traffic on Wade Avenue is usually heavy at this time of day, the route home is different from the route to work.

This new route is shown in Google Maps in Figure 9.4.

Figure 9.4: Shortest Path for Road Network at 5:00 P.M. in Google Maps