The Network Solver

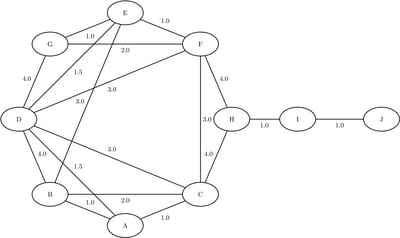
Consider the problem of designing a small network of computers in an office. In designing the network, the goal is to make sure that each machine in the office can reach every other machine. To accomplish this goal, Ethernet lines must be constructed and run between the machines. The construction costs for each possible link are based approximately on distance and are shown in Figure 9.74. Besides distance, the costs also reflect some restrictions due to physical boundaries. To connect all the machines in the office at minimal cost, you need to find a minimum spanning tree on the network of possible links.

Figure 9.74: Potential Office Computer Network

Define the link data set as follows:

data LinkSetInCompNet;
   input from $ to $ weight @@;
   datalines;
A B 1.0  A C 1.0  A D 1.5  B C 2.0  B D 4.0
B E 3.0  C D 3.0  C F 3.0  C H 4.0  D E 1.5
D F 3.0  D G 4.0  E F 1.0  E G 1.0  F G 2.0
F H 4.0  H I 1.0  I J 1.0
;

The following statements find a minimum spanning tree:

proc optmodel;
   set<str,str> LINKS;
   num weight{LINKS};
   read data LinkSetInCompNet into LINKS=[from to] weight;
   set<str,str> FOREST;

   solve with NETWORK /
      links       = (weight=weight)
      minspantree
      out         = (forest=FOREST)
   ;

   put FOREST;
   put (sum {<i,j> in FOREST} weight[i,j]);
   create data MinSpanTree from [from to]=FOREST weight;
quit;

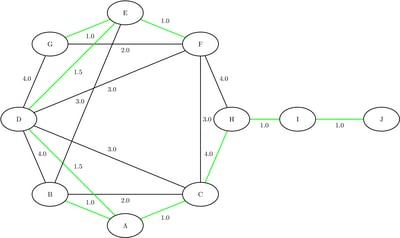
Output 9.5.1 shows the resulting data set MinSpanTree, which is displayed graphically in Figure 9.75 with the minimal cost links shown in green.

Figure 9.75: Minimum Spanning Tree for Office Computer Network