The Network Solver

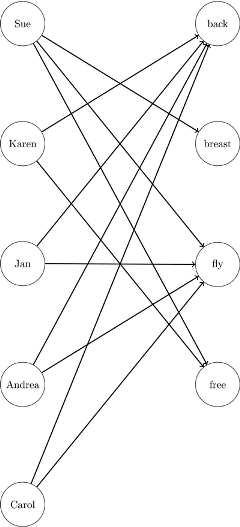
This example looks at the problem of assigning swimmers to strokes based on their best times. However, in this case certain swimmers are not eligible to perform certain strokes. A missing (.) value in the data matrix identifies an ineligible assignment. For example:

data RelayTimesMatrix;
   input name $ sex $ back breast fly free;
   datalines;
Sue     F   .  36.7 28.3 36.1
Karen   F 34.6    .    . 26.2
Jan     F 31.3    . 27.1    .
Andrea  F 28.6    . 29.1    .
Carol   F 32.9    . 26.6    .
;

Recall that the linear assignment problem can also be interpreted as the minimum-weight matching in a bipartite directed graph. The eligible assignments define links between the rows (swimmers) and the columns (strokes), as in Figure 9.72.

Figure 9.72: Bipartite Graph for Linear Assignment Problem

You can represent the same data in RelayTimesMatrix by using a links data set as follows:

data RelayTimesLinks;
   input name $ attr $ cost;
   datalines;
Sue     breast 36.7
Sue     fly    28.3
Sue     free   36.1
Karen   back   34.6
Karen   free   26.2
Jan     back   31.3
Jan     fly    27.1
Andrea  back   28.6
Andrea  fly    29.1
Carol   back   32.9
Carol   fly    26.6
;

This graph must be bipartite (such that S and T are disjoint). If it is not, the network solver returns an error.

Now, you can use either input format to solve the same problem, as follows:

proc contents data=RelayTimesMatrix
   out=stroke_data(rename=(name=stroke) where=(type=1));
run;

proc optmodel;
   set <str> STROKES;
   read data stroke_data into STROKES=[stroke];
   set <str> SWIMMERS;
   str sex {SWIMMERS};
   num time {SWIMMERS, STROKES};
   read data RelayTimesMatrix into SWIMMERS=[name]
      sex
      {stroke in STROKES} <time[name,stroke]=col(stroke)>;
   set SWIMMERS_STROKES =
      {name in SWIMMERS, stroke in STROKES: time[name,stroke] ne .};
   set <str,str> PAIRS;

   solve with NETWORK /
      graph_direction = directed
      links           = (weight=time)
      subgraph        = (links=SWIMMERS_STROKES)
      lap
      out             = (assignments=PAIRS)
   ;

   put PAIRS;
   create data LinearAssignMatrix from [name assign]=PAIRS
      sex[name] cost=time;
quit;

proc sql;
   create table stroke_data as
   select distinct attr as stroke
   from RelayTimesLinks;
quit;

proc optmodel;
   set <str> STROKES;
   read data stroke_data into STROKES=[stroke];
   set <str> SWIMMERS;
   str sex {SWIMMERS};
   set <str,str> SWIMMERS_STROKES;
   num time {SWIMMERS_STROKES};
   read data RelayTimesLinks into SWIMMERS_STROKES=[name attr] time=cost;
   set <str,str> PAIRS;

   solve with NETWORK /
      graph_direction = directed
      links           = (weight=time)
      lap
      out             = (assignments=PAIRS)
   ;

   put PAIRS;
   create data LinearAssignLinks from [name attr]=PAIRS cost=time;
quit;

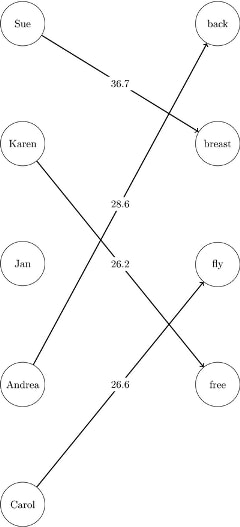
The data sets LinearAssignMatrix and LinearAssignLinks now contain the optimal assignments, as shown in Output 9.4.1 and Output 9.4.2.

The optimal assignments are shown graphically in Figure 9.73.

Figure 9.73: Optimal Assignments for Swim Times

For large problems where a number of links are forbidden, the sparse format can be faster and can save a great deal of memory. Consider an example that uses the dense format with 15,000 columns () and 4,000 rows (). To store the dense matrix in memory, the network solver needs to allocate approximately MB. If the data have mostly ineligible links, then the sparse (graph) format is much more efficient with respect to memory. For example, if the data have only 5% of the eligible links (), then the dense storage would still need 457 MB. The sparse storage for the same example needs approximately MB. If the problem is fully dense (all links are eligible), then the dense format is more efficient.