The Network Solver

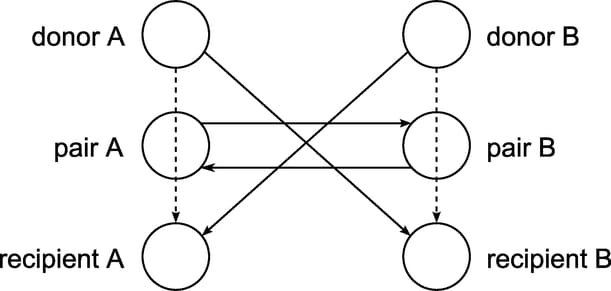
This example looks at an application of cycle detection to help create a kidney donor exchange. Suppose someone needs a kidney transplant and a family member is willing to donate one. If the donor and recipient are incompatible (because of blood types, tissue mismatch, and so on), the transplant cannot happen. Now suppose two donor-recipient pairs A and B are in this situation, but donor A is compatible with recipient B and donor B is compatible with recipient A. Then two transplants can take place in a two-way swap, shown graphically in Figure 9.71. More generally, an n-way swap can be performed involving n donors and n recipients (Willingham 2009).

Figure 9.71: Kidney Donor Exchange Two-Way Swap

To model this problem, define a directed graph as follows. Each node is an incompatible donor-recipient pair. Link exists if the donor from node i is compatible with the recipient from node j. The link weight is a measure of the quality of the match. By introducing dummy links whose weight is 0, you can also include altruistic donors who have no recipients or recipients who have no donors. The idea is to find a maximum-weight node-disjoint union of directed cycles. You want the union to be node-disjoint so that no kidney is donated more than once, and you want cycles so that the donor from node i gives up a kidney if and only if the recipient from node i receives a kidney.

Without any other constraints, the problem could be solved as a linear assignment problem, as described in the section Linear Assignment (Matching). But doing so would allow arbitrarily long cycles in the solution. Because of practical considerations (such as travel) and to mitigate risk, each cycle must have no more than L links. The kidney exchange problem is to find a maximum-weight node-disjoint union of short directed cycles.

One way to solve this problem is to explicitly generate all cycles whose length is at most L and then solve a set packing problem. You can use PROC OPTMODEL to generate the cycles, formulate the set packing problem, call the mixed integer linear programming solver, and output the optimal solution.

The following DATA step sets up the problem, first creating a random graph on n nodes with link probability p and Uniform(0,1) weight:

/* create random graph on n nodes with arc probability p
   and uniform(0,1) weight */
%let n = 100;
%let p = 0.02;
data LinkSetIn;
   do from = 0 to &n - 1;
      do to = 0 to &n - 1;
         if from eq to then continue;
         else if ranuni(1) < &p then do;
            weight = ranuni(2);
            output;
         end;
      end;
   end;
run;

The following statements declare parameters and then read the input data:

%let max_length = 10;
proc optmodel;
   /* declare index sets and parameters, and read data */
   set <num,num> ARCS;
   num weight {ARCS};
   read data LinkSetIn into ARCS=[from to] weight;
   set<num,num,num> ID_ORDER_NODE;

The following statements use the network solver to generate all cycles whose length is greater than or equal to 2 and less than or equal to 10:

   /* generate all cycles with 2 <= length <= max_length */
   solve with NETWORK /
      loglevel        = moderate
      graph_direction = directed
      links           = (include=ARCS)
      cycle           = (mode=all_cycles minlength=2 maxlength=&max_length)
      out             = (cycles=ID_ORDER_NODE)
   ;

The network solver finds 224 cycles of the appropriate length, as shown in Output 9.2.1.

NOTE: There were 194 observations read from the data set WORK.LINKSETIN.        
NOTE: The number of nodes in the input graph is 97.                             
NOTE: The number of links in the input graph is 194.                            
NOTE: Processing cycle detection.                                               
NOTE: The graph has 224 cycles.                                                 
NOTE: Processing cycle detection used 11.26 (cpu: 11.23) seconds.               

From the resulting set ID_ORDER_NODE, use the following statements to convert to one tuple per cycle-arc combination:

   /* extract <cid,from,to> triples from <cid,order,node> triples */
   set <num,num,num> ID_FROM_TO init {};
   num last init ., from, to;
   for {<cid,order,node> in ID_ORDER_NODE} do;
      from = last;
      to   = node;
      last = to;
      if order ne 1 then ID_FROM_TO = ID_FROM_TO union {<cid,from,to>};
   end;

Given the set of cycles, you can now formulate a mixed integer linear program (MILP) to maximize the total cycle weight. Let C be the set of cycles of appropriate length, be the set of nodes in cycle c, be the set of links in cycle c, and be the link weight for link . Define a binary decision variable . Set to 1 if cycle c is used in the solution; otherwise, set it to 0. Then, the following MILP defines the problem that you want to solve (to maximize the quality of the kidney exchange):

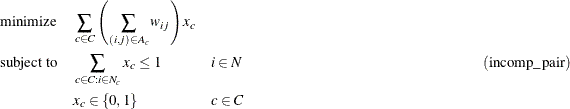
The constraint (incomp_pair) ensures that each node (incompatible pair) in the graph is intersected at most once. That is, a donor can donate a kidney only once. You can use PROC OPTMODEL to solve this mixed integer linear programming problem as follows:

   /* solve set packing problem to find maximum weight node-disjoint union
      of short directed cycles */
   set CYCLES = setof {<c,i,j> in ID_FROM_TO} c;
   set ARCS_c {c in CYCLES} = setof {<(c),i,j> in ID_FROM_TO} <i,j>;
   set NODES_c {c in CYCLES} = union {<i,j> in ARCS_c[c]} {i,j};
   set NODES = union {c in CYCLES} NODES_c[c];
   num cycle_weight {c in CYCLES} = sum {<i,j> in ARCS_c[c]} weight[i,j];

   /* UseCycle[c] = 1 if cycle c is used, 0 otherwise */
   var UseCycle {CYCLES} binary;

   /* declare objective */
   max TotalWeight
      = sum {c in CYCLES} cycle_weight[c] * UseCycle[c];

   /* each node appears in at most one cycle */
   con node_packing {i in NODES}:
      sum {c in CYCLES: i in NODES_c[c]} UseCycle[c] <= 1;

   /* call solver */
   solve with milp;

   /* output optimal solution */
   create data Solution from [c]={c in CYCLES: UseCycle[c].sol > 0.5}
      cycle_weight;
quit;
%put &_OROPTMODEL_;

PROC OPTMODEL solves the problem by using the mixed integer linear programming solver. As shown in Output 9.2.2, it was able to find a total weight (quality level) of 26.02.

NOTE: Problem generation will use 4 threads.                                    
NOTE: The problem has 224 variables (0 free, 0 fixed).                          
NOTE: The problem has 224 binary and 0 integer variables.                       
NOTE: The problem has 63 linear constraints (63 LE, 0 EQ, 0 GE, 0 range).       
NOTE: The problem has 1900 linear constraint coefficients.                      
NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range).      
NOTE: The MILP presolver value AUTOMATIC is applied.                            
NOTE: The MILP presolver removed 0 variables and 35 constraints.                
NOTE: The MILP presolver removed 634 constraint coefficients.                   
NOTE: The MILP presolver modified 0 constraint coefficients.                    
NOTE: The presolved problem has 224 variables, 28 constraints, and 1266         
      constraint coefficients.                                                  
NOTE: The MILP solver is called.                                                
          Node  Active    Sols    BestInteger      BestBound      Gap    Time   
             0       1       3     22.7780692   1080.2049611   97.89%       0   
             0       1       3     22.7780692     26.7803921   14.94%       0   
             0       1       3     22.7780692     26.0901734   12.69%       0   
             0       1       4     23.2158345     26.0202936   10.78%       0   
             0       1       4     23.2158345     26.0202886   10.78%       0   
             0       1       6     26.0202873     26.0202873    0.00%       0   
NOTE: The MILP solver added 8 cuts with 657 cut coefficients at the root.       
NOTE: Optimal.                                                                  
NOTE: Objective = 26.020287268.                                                 
NOTE: The data set WORK.SOLUTION has 6 observations and 2 variables.            
STATUS=OK ALGORITHM=BAC SOLUTION_STATUS=OPTIMAL OBJECTIVE=26.020287268          
RELATIVE_GAP=0 ABSOLUTE_GAP=0 PRIMAL_INFEASIBILITY=8.881784E-16                 
BOUND_INFEASIBILITY=0 INTEGER_INFEASIBILITY=4E-6 BEST_BOUND=26.020287268        
NODES=1 ITERATIONS=162 PRESOLVE_TIME=0.02 SOLUTION_TIME=0.12                    

The data set Solution, shown in Output 9.2.3, now contains the cycles that define the best exchange and their associated weight (quality).