The Network Solver
- Overview
- Getting Started
-
Syntax
-
DetailsInput Data for the Network SolverSolving over Subsets of Nodes and Links (Filters)Numeric LimitationsBiconnected Components and Articulation PointsCliqueConnected ComponentsCycleLinear Assignment (Matching)Minimum-Cost Network FlowMinimum CutMinimum Spanning TreeShortest PathTransitive ClosureTraveling Salesman ProblemMacro Variable _OROPTMODEL_
-
ExamplesArticulation Points in a Terrorist NetworkCycle Detection for Kidney Donor ExchangeLinear Assignment Problem for Minimizing Swim TimesLinear Assignment Problem, Sparse Format versus Dense FormatMinimum Spanning Tree for Computer Network TopologyTransitive Closure for Identification of Circular Dependencies in a Bug Tracking SystemTraveling Salesman Tour through US Capital Cities
- References
A shortest path between two nodes u and v in a graph is a path that starts at u and ends at v and has the lowest total link weight. The starting node is called the source node, and the ending node is called the sink node.
In the network solver, shortest paths can be calculated by invoking the SHORTPATH= option.
By default, the network solver finds shortest paths for all pairs. That is, it finds a shortest path for each possible combination of source and sink nodes. Alternatively, you can use the SOURCE= suboption to fix a particular source node and find shortest paths from the fixed source node to all possible sink nodes. Conversely, by using the SINK= suboption, you can fix a sink node and find shortest paths from all possible source nodes to the fixed sink node. Using both suboptions together, you can request one particular shortest path for a specific source-sink pair. In addition, you can use the SOURCE= and SINK= suboptions to define a list of source-sink pairs to process. The following sections show examples of these suboptions.
The algorithm that the network solver uses for finding shortest paths is a variant of Dijkstra’s algorithm (Ahuja, Magnanti,
and Orlin 1993). For unweighted graphs, the network solver uses a variant of breadth-first search. Dijkstra’s algorithm on weighted graphs
runs in time 
for each source node. Breadth-first search runs in time 
for each source node.
For weighted graphs, the algorithm uses the parameter that is specified in the WEIGHT= suboption of the SHORTPATH= option to evaluate a path’s total weight (cost).
The shortest path algorithm produces up to two outputs. The output set that is specified in the SPPATHS= suboption contains the links of a shortest path for each source-sink pair combination. The output parameter that is specified in the SPWEIGHTS= suboption contains the total weight for the shortest path for each source-sink pair combination.
This set contains the links present in the shortest path for each of the source-sink pairs.
The individual links in this set always appear in the order that you provide. If you provide link 
and solve a shortest path problem on an undirected graph, and that path visits node v before node u, then this set will contain link , not link 
, which is not part of the network. This approach simplifies indexing throughout your model. In certain use cases, especially
for producing output, you might prefer to see the links in the order in which the nodes are visited. For one way to do that,
see Example 9.7 Traveling Salesman Tour through US Capital Cities.
For large graphs and a large requested number of source-sink pairs, this set can be extremely large. For extremely large graphs, generating the output can sometimes take longer than computing the shortest paths. For example, using the US road network data for the state of New York, the data contain a directed graph that has 264,346 nodes. Finding the shortest path for all pairs from only one source node results in 140,969,120 observations, which is a set of size 11 GB. Finding shortest paths for all pairs from all nodes would produce an enormous set.
The SPPATHS= set contains the following tuple members:
-
the source node of this shortest path
-
the sink node of this shortest path
-
for this source-sink pair, the order of this link in a shortest path
-
the tail node of this link in a shortest path
-
the head node of this link in a shortest path
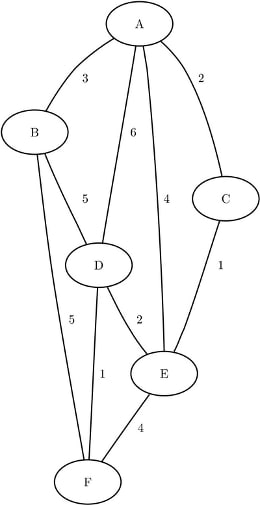
This example illustrates the use of the shortest path algorithm for all source-sink pairs on the simple undirected graph G that is shown in Figure 9.52.
The undirected graph G can be represented by the following links data set LinkSetIn:
data LinkSetIn; input from $ to $ weight @@; datalines; A B 3 A C 2 A D 6 A E 4 B D 5 B F 5 C E 1 D E 2 D F 1 E F 4 ;
The following statements calculate shortest paths for all source-sink pairs:
proc optmodel;
set <str,str> LINKS;
num weight{LINKS};
read data LinkSetIn into LINKS=[from to] weight;
set <str,str,num,str,str> PATHS; /* source, sink, order, from, to */
set NODES = union{<i,j> in LINKS} {i,j};
num path_length{NODES, NODES};
solve with NETWORK /
links = (weight=weight)
shortpath
out = (sppaths=PATHS spweights=path_length)
;
put PATHS;
print path_length;
create data ShortPathP from [source sink order from to]=PATHS
weight[from,to];
create data ShortPathW from [source sink]
path_weight=path_length;
quit;
The data set ShortPathP contains the shortest paths and is shown in Figure 9.53.
Figure 9.53: All-Pairs Shortest Paths
| ShortPathP |
| source | sink | order | from | to | weight |
|---|---|---|---|---|---|
| A | B | 1 | A | B | 3 |
| A | C | 1 | A | C | 2 |
| A | D | 1 | A | C | 2 |
| A | D | 2 | C | E | 1 |
| A | D | 3 | D | E | 2 |
| A | E | 1 | A | C | 2 |
| A | E | 2 | C | E | 1 |
| A | F | 1 | A | C | 2 |
| A | F | 2 | C | E | 1 |
| A | F | 3 | D | E | 2 |
| A | F | 4 | D | F | 1 |
| B | A | 1 | A | B | 3 |
| B | C | 1 | A | B | 3 |
| B | C | 2 | A | C | 2 |
| B | D | 1 | B | D | 5 |
| B | E | 1 | A | B | 3 |
| B | E | 2 | A | C | 2 |
| B | E | 3 | C | E | 1 |
| B | F | 1 | B | F | 5 |
| C | A | 1 | A | C | 2 |
| C | B | 1 | A | C | 2 |
| C | B | 2 | A | B | 3 |
| C | D | 1 | C | E | 1 |
| C | D | 2 | D | E | 2 |
| C | E | 1 | C | E | 1 |
| C | F | 1 | C | E | 1 |
| C | F | 2 | D | E | 2 |
| C | F | 3 | D | F | 1 |
| D | A | 1 | D | E | 2 |
| D | A | 2 | C | E | 1 |
| D | A | 3 | A | C | 2 |
| D | B | 1 | B | D | 5 |
| D | C | 1 | D | E | 2 |
| D | C | 2 | C | E | 1 |
| D | E | 1 | D | E | 2 |
| D | F | 1 | D | F | 1 |
| E | A | 1 | C | E | 1 |
| E | A | 2 | A | C | 2 |
| E | B | 1 | C | E | 1 |
| E | B | 2 | A | C | 2 |
| E | B | 3 | A | B | 3 |
| E | C | 1 | C | E | 1 |
| E | D | 1 | D | E | 2 |
| E | F | 1 | D | E | 2 |
| E | F | 2 | D | F | 1 |
| F | A | 1 | D | F | 1 |
| F | A | 2 | D | E | 2 |
| F | A | 3 | C | E | 1 |
| F | A | 4 | A | C | 2 |
| F | B | 1 | B | F | 5 |
| F | C | 1 | D | F | 1 |
| F | C | 2 | D | E | 2 |
| F | C | 3 | C | E | 1 |
| F | D | 1 | D | F | 1 |
| F | E | 1 | D | F | 1 |
| F | E | 2 | D | E | 2 |
The data set ShortPathW contains the path weight for the shortest paths of each source-sink pair and is shown in Figure 9.54.
When you are interested only in the source-sink pair that has the longest shortest path, you can use the PATHS= suboption. This suboption affects only the output processing; it does not affect the computation. All the designated source-sink shortest paths are calculated, but only the longest ones are written to the output set.
The following statements display only the longest shortest paths:
proc optmodel;
set <str,str> LINKS;
num weight{LINKS};
read data LinkSetIn into LINKS=[from to] weight;
set <str,str,num,str,str> PATHS; /* source, sink, order, from, to */
solve with NETWORK /
links = ( weight = weight )
shortpath = ( paths = longest )
out = ( sppaths = PATHS )
;
put PATHS;
create data ShortPathLong from [source sink order from to]=PATHS
weight[from,to];
quit;
The data set ShortPathLong now contains the longest shortest paths and is shown in Figure 9.55.
This section illustrates the use of the SOURCE= and SINK= suboptions and the shortest path algorithm for calculating shortest paths between a subset of source-sink pairs. If S denotes the nodes in the SOURCE= set and T denotes the nodes in the SINK= set, the network solver calculates all the source-sink pairs in the cross product of these two sets.
For example, the following statements calculate a shortest path for the four combinations of source-sink pairs in 
:
proc optmodel;
set <str,str> LINKS;
num weight{LINKS};
read data LinkSetIn into LINKS=[from to] weight;
set <str,str,num,str,str> PATHS; /* source, sink, order, from, to */
set SOURCES = / A C /;
set SINKS = / B F /;
solve with NETWORK /
links = (weight=weight)
shortpath = (source=SOURCES sink=SINKS)
out = (sppaths=PATHS)
;
put PATHS;
create data ShortPath from [source sink order from to]=PATHS weight[from,to];
quit;
The data set ShortPath contains the shortest paths and is shown in Figure 9.56.
This section illustrates the use of the shortest path algorithm for calculating shortest paths between a subset of source (or sink) nodes and all other sink (or source) nodes.
In this case, you designate the subset of source (or sink) nodes in the node set by specifying the SOURCE= (or SINK=) suboption. By specifying only one of the suboptions, you indicate that you want the network solver to calculate all pairs from a subset of source nodes (or to calculate all pairs to a subset of sink nodes).
For example, the following statements calculate all the shortest paths from nodes B and E.:
proc optmodel;
set <str,str> LINKS;
num weight{LINKS};
read data LinkSetIn into LINKS=[from to] weight;
set <str,str,num,str,str> PATHS; /* source, sink, order, from, to */
set SOURCES = / B E /;
solve with NETWORK /
links = (weight=weight)
shortpath = (source=SOURCES)
out = (sppaths=PATHS)
;
put PATHS;
create data ShortPath from [source sink order from to]=PATHS weight[from,to];
quit;
The data set ShortPath contains the shortest paths and is shown in Figure 9.57.
Conversely, the following statements calculate all the shortest paths to nodes B and E.:
proc optmodel;
set <str,str> LINKS;
num weight{LINKS};
read data LinkSetIn into LINKS=[from to] weight;
set <str,str,num,str,str> PATHS; /* source, sink, order, from, to */
set SINKS = / B E /;
solve with NETWORK /
links = (weight=weight)
shortpath = (sink=SINKS)
out = (sppaths=PATHS)
;
put PATHS;
create data ShortPath from [source sink order from to]=PATHS weight[from,to];
quit;
The data set ShortPath contains the shortest paths and is shown in Figure 9.58.
This section illustrates the use of the shortest path algorithm for calculating shortest paths between one source-sink pair by using the SOURCE= and SINK= suboptions.
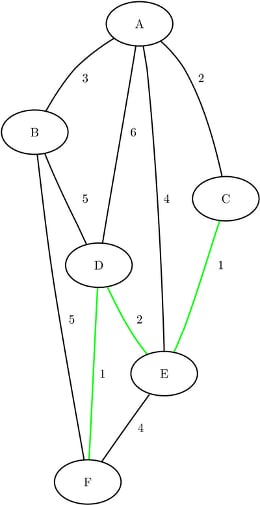
The following statements calculate a shortest path between node C and node F:
proc optmodel;
set <str,str> LINKS;
num weight{LINKS};
read data LinkSetIn into LINKS=[from to] weight;
set <str,str,num,str,str> PATHS; /* source, sink, order, from, to */
set SOURCES = / C /;
set SINKS = / F /;
solve with NETWORK /
links = (weight=weight)
shortpath = (source=SOURCES sink=SINKS)
out = (sppaths=PATHS)
;
put PATHS;
create data ShortPath from [source sink order from to]=PATHS weight[from,to];
quit;
The data set ShortPath contains this shortest path and is shown in Figure 9.59.
The shortest path is shown graphically in Figure 9.60.
This section illustrates the use of the shortest path algorithm, where auxiliary weights are used for calculating the shortest paths between all source-sink pairs.
Consider a links data set in which the auxiliary weight is a counter for each link:
data LinkSetIn; input from $ to $ weight count @@; datalines; A B 3 1 A C 2 1 A D 6 1 A E 4 1 B D 5 1 B F 5 1 C E 1 1 D E 2 1 D F 1 1 E F 4 1 ;
The following statements calculate shortest paths for all source-sink pairs:
proc optmodel;
set <str,str> LINKS;
num weight{LINKS};
num count{LINKS};
read data LinkSetIn into LINKS=[from to] weight count;
set <str,str,num,str,str> PATHS; /* source, sink, order, from, to */
set NODES = union{<i,j> in LINKS} {i,j};
num path_length{NODES, NODES};
solve with NETWORK /
links = (weight=weight)
shortpath
out = (sppaths=PATHS spweights=path_length)
;
put PATHS;
num path_weight2{source in NODES, sink in NODES} =
sum {<(source),(sink),order,from,to> in PATHS} count[from,to];
print path_length path_weight2;
create data ShortPathW from [source sink]
path_weight=path_length path_weight2;
quit;
The data set ShortPathW contains the total path weight for shortest paths in each source-sink pair and is shown in Figure 9.61. Because the variable count in LinkSetIn is 1 for all links, the value in the output data set variable path_weights2 contains the number of links in each shortest path.
Figure 9.61: Shortest Paths Including Auxiliary Weights in Calculation
| ShortPathW |
| source | sink | path_weight | path_weight2 |
|---|---|---|---|
| A | A | . | 0 |
| A | B | 3 | 1 |
| A | C | 2 | 1 |
| A | D | 5 | 3 |
| A | E | 3 | 2 |
| A | F | 6 | 4 |
| B | A | 3 | 1 |
| B | B | . | 0 |
| B | C | 5 | 2 |
| B | D | 5 | 1 |
| B | E | 6 | 3 |
| B | F | 5 | 1 |
| C | A | 2 | 1 |
| C | B | 5 | 2 |
| C | C | . | 0 |
| C | D | 3 | 2 |
| C | E | 1 | 1 |
| C | F | 4 | 3 |
| D | A | 5 | 3 |
| D | B | 5 | 1 |
| D | C | 3 | 2 |
| D | D | . | 0 |
| D | E | 2 | 1 |
| D | F | 1 | 1 |
| E | A | 3 | 2 |
| E | B | 6 | 3 |
| E | C | 1 | 1 |
| E | D | 2 | 1 |
| E | E | . | 0 |
| E | F | 3 | 2 |
| F | A | 6 | 4 |
| F | B | 5 | 1 |
| F | C | 4 | 3 |
| F | D | 1 | 1 |
| F | E | 3 | 2 |
| F | F | . | 0 |
The section Getting Started: Network Solver shows an example of using the shortest path algorithm for minimizing travel to and from work based on traffic conditions.