The MI Procedure

Monotone and FCS Discriminant Function Methods

Pooled Covariance Matrix and Group-Specific Means
Prior Probabilities of Group Membership
Imputation Steps

The discriminant function method is the default imputation method in the MONOTONE and FCS statements for classification variables.

For a nominal classification variable $Y_{j}$ with responses 1, …, g and a set of effects from its preceding variables, if the covariates $X_{1}$ , $X_{2}$ , …, $X_{k}$ associated with these effects within each group are approximately multivariate normal and the within-group covariance matrices are approximately equal, the discriminant function method (Brand, 1999, pp. 95–96) can be used to impute missing values for the variable $Y_{j}$ .

Denote the group-specific means for covariates $X_{1}$ , $X_{2}$ , …, $X_{k}$ by

$\overline{\mb {X}}_{t} = ( \overline{X}_{t1}, \overline{X}_{t2}, \ldots , \overline{X}_{tk} ), \, t= 1, 2, \ldots , g$

then the pooled covariance matrix is computed as

$\mb {S} = \frac{1}{n-g} \sum _{t=1}^{g} (n_{t}-1) \mb {S}_{t}$

where $\mb {S}_{t}$ is the within-group covariance matrix, $n_{t}$ is the group-specific sample size, and $n= \sum _{t=1}^{g} n_{t}$ is the total sample size.

In each imputation, new parameters of the group-specific means ( $\mb {m}_{*t}$ ), pooled covariance matrix ( $\mb {S}_{*}$ ), and prior probabilities of group membership ( $q_{*t}$ ) can be drawn from their corresponding posterior distributions (Schafer, 1997, p. 356).

Pooled Covariance Matrix and Group-Specific Means

For each imputation, the MI procedure uses either the fixed observed pooled covariance matrix (PCOV=FIXED) or a drawn pooled covariance matrix (PCOV=POSTERIOR) from its posterior distribution with a noninformative prior. That is,

$\displaystyle \bSigma | \Strong{X} \quad \sim$

$\displaystyle$

$\displaystyle W^{-1} \left( \, n-g, \, (n-g)\Strong{S} \right)$

where $W^{-1}$ is an inverted Wishart distribution.

The group-specific means are then drawn from their posterior distributions with a noninformative prior

$\displaystyle \bmu _{t} | ( \bSigma , \overline{\Strong{X}}_{t}) \quad \sim$

$\displaystyle$

$\displaystyle N \left( \, \overline{\Strong{X}}_{t}, \, \, \frac{1}{\, n_{t} \, } \bSigma \right)$

See the section Bayesian Estimation of the Mean Vector and Covariance Matrix for a complete description of the inverted Wishart distribution and posterior distributions that use a noninformative prior.

Prior Probabilities of Group Membership

The prior probabilities are computed through the drawing of new group sample sizes. When the total sample size n is considered fixed, the group sample sizes $(n_{1}, n_{2}, \ldots , n_{g})$ have a multinomial distribution. New multinomial parameters (group sample sizes) can be drawn from their posterior distribution by using a Dirichlet prior with parameters $({\alpha }_{1}, {\alpha }_{2}, \ldots , {\alpha }_{g})$ .

After the new sample sizes are drawn from the posterior distribution of $(n_{1}, n_{2}, \ldots , n_{g})$ , the prior probabilities $q_{*t}$ are computed proportionally to the drawn sample sizes.

See Schafer (1997, pp. 247–255) for a complete description of the Dirichlet prior.

Imputation Steps

The discriminant function method uses the following steps in each imputation to impute values for a nominal classification variable $Y_{j}$ with g responses:

Draw a pooled covariance matrix 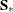$\mb {S}_{*}$ from its posterior distribution if the PCOV=POSTERIOR option is used.
For each group, draw group means 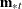$\mb {m}_{*t}$ from the observed group mean 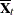$\overline{\mb {X}}_{t}$ and either the observed pooled covariance matrix (PCOV=FIXED) or the drawn pooled covariance matrix 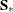$\mb {S}_{*}$ (PCOV=POSTERIOR).
For each group, compute or draw 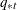$q_{*t}$ , prior probabilities of group membership, based on the PRIOR= option:
- PRIOR=EQUAL, 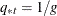$q_{*t}=1/g$ , prior probabilities of group membership are all equal.
- PRIOR=PROPORTIONAL, 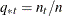$q_{*t}=n_{t}/n$ , prior probabilities are proportional to their group sample sizes.
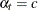- PRIOR=JEFFREYS= $\Argument{c}$ , a noninformative Dirichlet prior with ${\alpha }_{t}=c$ is used.
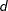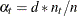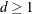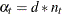- PRIOR=RIDGE= $\Argument{d}$ , a ridge prior is used with ${\alpha }_{t} = d * n_{t}/n$ for $d \geq 1$ and ${\alpha }_{t} = d * n_{t}$ for .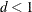

With the group means 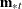$\mb {m}_{*t}$ , the pooled covariance matrix 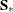$\mb {S}_{*}$ , and the prior probabilities of group membership 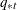$q_{*t}$ , the discriminant function method derives linear discriminant function and computes the posterior probabilities of an observation belonging to each group

$p_{t}(\mb {x}) = \frac{ \mr {exp}(-0.5 D_{t}^{2}(\mb {x}) )}{ \sum _{u=1}^{g} \mr {exp}(-0.5 D_{u}^{2}(\mb {x}) )}$

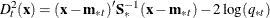where $D_{t}^{2}(\mb {x}) = {(\mb {x}-\mb {m}_{*t})}^{\prime } \mb {S}_{*}^{-1} (\mb {x}-\mb {m}_{*t}) - 2 \, \mr {log}(q_{*t})$ is the generalized squared distance from $\mb {x}$ to group t.

Draw a random uniform variate u, between 0 and 1, for each observation with missing group value. With the posterior probabilities, 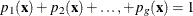$p_{1}(\mb {x}) + p_{2}(\mb {x}) + \ldots , + p_{g}(\mb {x}) = 1$ , the discriminant function method imputes 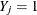$Y_{j}= 1$ if the value of u is less than 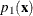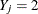$p_{1}(\mb {x})$ , $Y_{j}= 2$ if the value is greater than or equal to 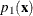$p_{1}(\mb {x})$ but less than 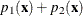$p_{1}(\mb {x})+p_{2}(\mb {x})$ , and so on.