The MI Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Descriptive StatisticsEM Algorithm for Data with Missing ValuesStatistical Assumptions for Multiple ImputationMissing Data PatternsImputation MethodsMonotone Methods for Data Sets with Monotone Missing PatternsMonotone and FCS Regression MethodsMonotone and FCS Predictive Mean Matching MethodsMonotone Propensity Score MethodMonotone and FCS Discriminant Function MethodsMonotone and FCS Logistic Regression MethodsFCS Methods for Data Sets with Arbitrary Missing PatternsChecking Convergence in FCS MethodsMCMC Method for Arbitrary Missing Multivariate Normal DataProducing Monotone Missingness with the MCMC MethodMCMC Method SpecificationsChecking Convergence in MCMCInput Data SetsOutput Data SetsCombining Inferences from Multiply Imputed Data SetsMultiple Imputation EfficiencyImputer’s Model Versus Analyst’s ModelParameter Simulation versus Multiple ImputationSummary of Issues in Multiple ImputationODS Table NamesODS Graphics
Descriptive StatisticsEM Algorithm for Data with Missing ValuesStatistical Assumptions for Multiple ImputationMissing Data PatternsImputation MethodsMonotone Methods for Data Sets with Monotone Missing PatternsMonotone and FCS Regression MethodsMonotone and FCS Predictive Mean Matching MethodsMonotone Propensity Score MethodMonotone and FCS Discriminant Function MethodsMonotone and FCS Logistic Regression MethodsFCS Methods for Data Sets with Arbitrary Missing PatternsChecking Convergence in FCS MethodsMCMC Method for Arbitrary Missing Multivariate Normal DataProducing Monotone Missingness with the MCMC MethodMCMC Method SpecificationsChecking Convergence in MCMCInput Data SetsOutput Data SetsCombining Inferences from Multiply Imputed Data SetsMultiple Imputation EfficiencyImputer’s Model Versus Analyst’s ModelParameter Simulation versus Multiple ImputationSummary of Issues in Multiple ImputationODS Table NamesODS Graphics -
Examples
 EM Algorithm for MLEMonotone Propensity Score MethodMonotone Regression MethodMonotone Logistic Regression Method for CLASS VariablesMonotone Discriminant Function Method for CLASS VariablesFCS Method for Continuous VariablesFCS Method for CLASS VariablesFCS Method with Trace PlotMCMC MethodProducing Monotone Missingness with MCMCChecking Convergence in MCMCSaving and Using Parameters for MCMCTransforming to NormalityMultistage Imputation
EM Algorithm for MLEMonotone Propensity Score MethodMonotone Regression MethodMonotone Logistic Regression Method for CLASS VariablesMonotone Discriminant Function Method for CLASS VariablesFCS Method for Continuous VariablesFCS Method for CLASS VariablesFCS Method with Trace PlotMCMC MethodProducing Monotone Missingness with MCMCChecking Convergence in MCMCSaving and Using Parameters for MCMCTransforming to NormalityMultistage Imputation - References
Monotone and FCS Logistic Regression Methods
The logistic regression method is another imputation method available for classification variables. In the logistic regression method, a logistic regression model is fitted for a classification variable with a set of covariates constructed from the effects. For a binary classification variable, based on the fitted regression model, a new logistic regression model is simulated from the posterior predictive distribution of the parameters and is used to impute the missing values for each variable (Rubin, 1987, pp. 167–170).
For a binary variable ![]() with responses 1 and 2, a logistic regression model is fitted using observations with observed values for the imputed variable
with responses 1 and 2, a logistic regression model is fitted using observations with observed values for the imputed variable
![]() and its covariates
and its covariates ![]() ,
, ![]() , …,
, …, ![]() :
:
|
|
where ![]() are covariates for
are covariates for ![]() ,
, ![]() , and
, and ![]()
The fitted model includes the regression parameter estimates ![]() and the associated covariance matrix
and the associated covariance matrix ![]() .
.
The following steps are used to generate imputed values for a binary variable ![]() with responses 1 and 2:
with responses 1 and 2:
-
New parameters
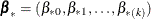 are drawn from the posterior predictive distribution of the parameters.
are drawn from the posterior predictive distribution of the parameters.
![\[ \bbeta _{*} = \hat{\bbeta } + \mb {V}_{hj}’ \mb {Z} \]](images/statug_mi0167.png)
where
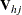 is the upper triangular matrix in the Cholesky decomposition,
is the upper triangular matrix in the Cholesky decomposition, 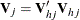 , and
, and 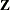 is a vector of
is a vector of 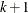 independent random normal variates.
independent random normal variates.
-
For an observation with missing
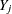 and covariates
and covariates 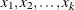 , compute the expected probability that
, compute the expected probability that 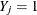 :
:
![\[ p_{j} = \frac{\mr {exp}({\mu }_ j)}{1+\mr {exp}({\mu }_ j)} \]](images/statug_mi0168.png)
where
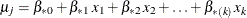 .
.
-
Draw a random uniform variate, u, between 0 and 1. If the value of u is less than
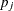 , impute
, impute 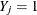 ; otherwise impute
; otherwise impute 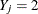 .
.
The preceding logistic regression method can be extended to include the ordinal classification variables with more than two levels of responses. The options ORDER= and DESCENDING can be used to specify the sort order for the levels of the imputed variables.