The PHREG Procedure

The Multiplicative Hazards Model

Consider a set of n subjects such that the counting process $N_ i \equiv \{ N_ i(t), t \geq 0\}$ for the ith subject represents the number of observed events experienced over time t. The sample paths of the process are step functions with jumps of size , with . Let $\bbeta$ denote the vector of unknown regression coefficients. The multiplicative hazards function $\Lambda (t,{\bZ }_{i}(t))$ for $N_{i}$ is given by

$Y_{i}(t)d\Lambda (t,{\bZ }_{i}(t)) = Y_{i}(t)\exp (\bbeta ’\bZ _{i}(t)) d\Lambda _{0}(t)$

where

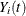indicates whether the ith subject is at risk at time t (specifically, 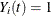if at risk and 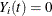otherwise)
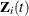$\bZ _ i(t)$ is the vector of explanatory variables for the ith subject at time t
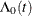$\Lambda _{0}(t)$ is an unspecified baseline hazard function

See Fleming and Harrington (1991) and Andersen et al. (1992). The Cox model is a special case of this multiplicative hazards model, where until the first event or censoring, and thereafter.

The partial likelihood for n independent triplets $(N_{i},Y_{i},{\bZ }_{i}), i=1, \ldots , n$ , has the form

$\mc {L}(\bbeta ) = \prod _{i=1}^{n} \prod _{t \geq 0} \biggl \{ \frac{Y_{i}(t)\exp (\bbeta \bZ _{i}(t))}{\sum _{j=1}^{n}Y_{j}(t)\exp (\bbeta \bZ _{j}(t))} \biggr \} ^{\Delta N_{i}(t)}$

where $\Delta N_{i}(t) = 1$ if $N_{i}(t) - N_{i}(t-) = 1$ , and $\Delta N_{i}(t) = 0$ otherwise.