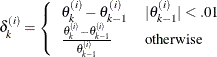The PHREG Procedure

MODEL Statement

MODEL response <*censor (list)> = effects </ options> ;

MODEL (t1, t2)<*censor(list)> = effects </ options> ;

The MODEL statement identifies the variables to be used as the failure time variables, the optional censoring variable, and the explanatory effects, including covariates, main effects, interactions, nested effects; see the section Specification of Effects of Chapter 42: The GLM Procedure, for more information. A note of caution: specifying the effect T*A in the MODEL statement, where T is the time variable and A is a CLASS variable, does not make the effect time-dependent. See the section Time and CLASS Variables Usage for more information.

Two forms of MODEL syntax can be specified; the first form allows one time variable, and the second form allows two time variables for the counting process style of input (see the section Counting Process Style of Input for more information).

In the first MODEL statement, the name of the failure time variable precedes the equal sign. This name can optionally be followed by an asterisk, the name of the censoring variable, and a list of censoring values (separated by blanks or commas if there is more than one) enclosed in parentheses. If the censoring variable takes on one of these values, the corresponding failure time is considered to be censored. Following the equal sign are the explanatory effects (sometimes called independent variables or covariates) for the model.

Instead of a single failure-time variable, the second MODEL statement identifies a pair of failure-time variables. Their names are enclosed in parentheses, and they signify the endpoints of a semiclosed interval during which the subject is at risk. If the censoring variable takes on one of the censoring values, the time t2 is considered to be censored.

The censoring variable must be numeric and the failure-time variables must contain nonnegative values. Any observation with a negative failure time is excluded from the analysis, as is any observation with a missing value for any of the variables listed in the MODEL statement. Failure-time variables with a SAS date format are not recommended because the dates might be translated into negative numbers and consequently the corresponding observation would be discarded.

Table 67.10 summarizes the options available in the MODEL statement. These options can be specified after a slash (/). Four convergence criteria are allowed for the maximum likelihood optimization: ABSFCONV=, FCONV=, GCONV=, and XCONV=. If you specify more than one convergence criterion, the optimization is terminated as soon as one of the criteria is satisfied. If none of the criteria is specified, the default is GCONV=1E–8.

Table 67.10: MODEL Statement Options

Option	Description
Model Specification Options
NOFIT	Suppresses model fitting
OFFSET=	Specifies offset variable
SELECTION=	Specifies effect selection method
Effect Selection Options
BEST=	Controls the number of models displayed for SCORE selection
DETAILS	Requests detailed results at each step
HIERARCHY=	Specifies whether and how hierarchy is maintained and whether a single effect or multiple effects are allowed to enter or leave the model per step
INCLUDE=	Specifies number of effects included in every model
MAXSTEP=	Specifies maximum number of steps for STEPWISE selection
SEQUENTIAL	Adds or deletes effects in sequential order
SLENTRY=	Specifies significance level for entering effects
SLSTAY=	Specifies significance level for removing effects
START=	Specifies number of variables in first model
STOP=	Specifies number of variables in final model
STOPRES	Adds or deletes variables by residual chi-square criterion
Maximum Likelihood Optimization Options
ABSFCONV=	Specifies absolute function convergence criterion
FCONV=	Specifies relative function convergence criterion
FIRTH	Specifies Firth’s penalized likelihood method
GCONV=	Specifies relative gradient convergence criterion
XCONV=	Specifies relative parameter convergence criterion
MAXITER=	Specifies maximum number of iterations
RIDGEINIT=	Specifies the initial ridging value
RIDGING=	Specifies the technique to improve the log likelihood function when its value is worse than that of the previous step
SINGULAR=	Specifies tolerance for testing singularity
Confidence Interval Options
ALPHA=	Specifies $\alpha$ for the $100(1-\alpha )\%$ confidence intervals
PLCONV=	Specifies profile-likelihood convergence criterion
RISKLIMITS=	Computes confidence intervals for hazard ratios
Display Options
CORRB	Displays correlation matrix
COVB	Displays covariance matrix
ITPRINT	Displays iteration history
NODUMMYPRINT	Suppresses “Class Level Information” table
TYPE1	Displays Type 1 analysis
TYPE3	Displays Type 3 analysis
Miscellaneous Options
ENTRYTIME=	Specifies the delayed entry time variable
TIES=	Specifies the method of handling ties in failure times

ALPHA=value

sets the significance level used for the confidence limits for the hazard ratios. The quantity value must be between 0 and 1. The default is the value of the ALPHA= option in the PROC PHREG statement, or 0.05 if that option is not specified. This option has no effect unless the RISKLIMITS option is specified.

ABSFCONV=value CONVERGELIKE=value

specifies the absolute function convergence criterion. Termination requires a small change in the objective function (log partial likelihood function) in subsequent iterations,

$|l_ k - l_{k-1}| < \Argument{value}$

where is the value of the objective function at iteration k.

BEST=n

is used exclusively with the SCORE model selection method. The BEST=n option specifies that n models with the highest-score chi-square statistics are to be displayed for each model size. If the option is omitted and there are no more than 10 explanatory variables, then all possible models are listed for each model size. If the option is omitted and there are more than 10 explanatory variables, then the number of models selected for each model size is, at most, equal to the number of explanatory variables listed in the MODEL statement.

See Example 67.2 for an illustration of the SCORE selection method and the BEST= option.

CORRB

displays the estimated correlation matrix of the parameter estimates.

COVB

displays the estimated covariance matrix of the parameter estimates.

DETAILS

produces a detailed display at each step of the model-building process. It produces an “Analysis of Variables Not in the Model” table before displaying the variable selected for entry for FORWARD or STEPWISE selection. For each model fitted, it produces the “Analysis of Maximum Likelihood Estimates” table.

See Example 67.1 for a discussion of these tables.

ENTRYTIME=variable ENTRY=variable

specifies the name of the variable that represents the left-truncation time. This option has no effect when the counting process style of input is specified. See the section Left-Truncation of Failure Times for more information.

FCONV=value

specifies the relative function convergence criterion. Termination requires a small relative change in the objective function (log partial likelihood function) in subsequent iterations,

$\frac{|l_ k - l_{k-1}|}{|l_{k-1}| + 1\mr {E}-6} < \Argument{value}$

where is the value of the objective function at iteration k.

FIRTH

performs Firth’s penalized maximum likelihood estimation to reduce bias in the parameter estimates (Heinze and Schemper, 2001; Firth, 1993). This method is useful when the likelihood is monotone—that is, the likelihood converges to finite value while at least one estimate diverges to infinity.

GCONV=value

specifies the relative gradient convergence criterion. Termination requires that the normalized prediction function reduction is small,

$\frac{\mb {g}_ k \mb {H}^{-1}_ k \mb {g}_ k}{|l_ k| + 1\mr {E}-6} < \Argument{value}$

where is the log partial likelihood, $\mb {g}_ k$ is the gradient vector (first partial derivatives of the log partial likelihood), and $\mb {H}_ k$ is the negative Hessian matrix (second partial derivatives of the log partial likelihood), all at iteration k.

HIERARCHY=keyword HIER=keyword

specifies whether and how the model hierarchy requirement is applied and whether a single effect or multiple effects are allowed to enter or leave the model in one step. You can specify that only CLASS variable effects, or both CLASS and continuous variable effects, be subject to the hierarchy requirement. The HIERARCHY= option is ignored unless you also specify the FORWARD, BACKWARD, or STEPWISE selection method.

Model hierarchy refers to the requirement that, for any term to be in the model, all effects contained in the term must be present in the model. For example, in order for the interaction A*B to enter the model, the main effects A and B must be in the model. Likewise, neither effect A nor B can leave the model while the interaction A*B is in the model.

You can specify any of the following keywords in the HIERARCHY= option:

NONE: indicates that the model hierarchy is not maintained. Any single effect can enter or leave the model at any given step of the selection process.
SINGLE: indicates that only one effect can enter or leave the model at one time, subject to the model hierarchy requirement. For example, suppose that you specify the main effects A and B and the interaction of A*B in the model. In the first step of the selection process, either A or B can enter the model. In the second step, the other main effect can enter the model. The interaction effect can enter the model only when both main effects have already been entered. Also, before A or B can be removed from the model, the A*B interaction must first be removed. All effects (CLASS and continuous variables) are subject to the hierarchy requirement.
SINGLECLASS: is the same as HIERARCHY=SINGLE except that only CLASS effects are subject to the hierarchy requirement.
MULTIPLE: indicates that more than one effect can enter or leave the model at one time, subject to the model hierarchy requirement. In a forward selection step, a single main effect can enter the model, or an interaction can enter the model together with all the effects that are contained in the interaction. In a backward elimination step, an interaction itself, or the interaction together with all the effects that the interaction contains, can be removed. All effects (CLASS and continuous variable) are subject to the hierarchy requirement.
MULTIPLECLASS: is the same as HIERARCHY=MULTIPLE except that only CLASS effects are subject to the hierarchy requirement.

The default value is HIERARCHY=SINGLE, which means that model hierarchy is to be maintained for all effects (that is, both CLASS and continuous variable effects) and that only a single effect can enter or leave the model at each step.

INCLUDE=n

includes the first n effects in the MODEL statement in every model. By default, INCLUDE=0. The INCLUDE= option has no effect when SELECTION=NONE.

ITPRINT

displays the iteration history, including the last evaluation of the gradient vector.

MAXITER=n

specifies the maximum number of iterations allowed. The default value for n is 25. If convergence is not attained in n iterations, the displayed output and all data sets created by PROC PHREG contain results that are based on the last maximum likelihood iteration.

MAXSTEP=n

specifies the maximum number of times the explanatory variables can move in and out of the model before the STEPWISE model-building process ends. The default value for n is twice the number of explanatory variables in the MODEL statement. The option has no effect for other model selection methods.

NODUMMYPRINT NODESIGNPRINT NODP

suppresses the “Class Level Information” table, which shows how the design matrix columns for the CLASS variables are coded.

NOFIT

performs the global score test, which tests the joint significance of all the explanatory variables in the MODEL statement. No parameters are estimated. If the NOFIT option is specified along with other MODEL statement options, NOFIT takes precedence, and all other options are ignored except the TIES= option.

OFFSET=name

specifies the name of an offset variable, which is an explanatory variable with a regression coefficient fixed as one. This option can be used to incorporate risk weights for the likelihood function.

PLCONV=value

controls the convergence criterion for confidence intervals based on the profile-likelihood function. The quantity value must be a positive number, with a default value of 1E–4. The PLCONV= option has no effect if profile-likelihood based confidence intervals are not requested.

RIDGING=keyword

specifies the technique to improve the log likelihood when its value is worse than that of the previous step. The available keywords are as follows:

ABSOLUTE: specifies that the diagonal elements of the negative (expected) Hessian be inflated by adding the ridge value.
RELATIVE: specifies that the diagonal elements be inflated by the factor equal to 1 plus the ridge value.
NONE: specifies the crude line-search method of taking half a step be used instead of ridging.

The default is RIDGING=RELATIVE.

RIDGEINIT=value

specifies the initial ridge value. The maximum ridge value is 2000 times the maximum of 1 and the initial ridge value. The initial ridge value is raised to 1E–4 if it is less than 1E–4. By default, RIDGEINIT=1E–4. This option has no effect for RIDGING=ABSOLUTE.

RISKLIMITS<=keyword> RL<=keyword>

produces confidence intervals for hazard ratios of main effects not involved in interactions or nestings. Computation of these confidence intervals is based on the profile likelihood or based on individual Wald tests. The confidence coefficient can be specified with the ALPHA= option. You can specify one of the following keywords:

PL: requests profile-likelihood confidence limits.
WALD: requests confidence limits based on the Wald tests.
BOTH: request both profile-likelihood and Wald confidence limits.

Classification main effects that use parameterizations other than REF, EFFECT, or GLM are ignored. If you need to compute hazard ratios for an effect involved in interactions or nestings, or using some other parameterization, then you should specify a HAZARDRATIO statement for that effect.

SELECTION=method

specifies the method used to select the model. The methods available are as follows:

BACKWARD B: requests backward elimination.
FORWARD F: requests forward selection.
NONE N: fits the complete model specified in the MODEL statement. This is the default value.
SCORE: requests best subset selection. It identifies a specified number of models with the highest-score chi-square statistic for all possible model sizes ranging from one explanatory variable to the total number of explanatory variables listed in the MODEL statement. This option is not allowed if an explanatory effect in the MODEL statement contains a CLASS variable.
STEPWISE S: requests stepwise selection.

For more information, see the section Effect Selection Methods.

SEQUENTIAL

forces variables to be added to the model in the order specified in the MODEL statement or to be eliminated from the model in the reverse order of that specified in the MODEL statement.

SINGULAR=value

specifies the singularity criterion for determining linear dependencies in the set of explanatory variables. The default value is 1E–12.

SLENTRY=value SLE=value

specifies the significance level (a value between 0 and 1) for entering an explanatory variable into the model in the FORWARD or STEPWISE method. For all variables not in the model, the one with the smallest p-value is entered if the p-value is less than or equal to the specified significance level. The default value is 0.05.

SLSTAY=value

SLS=value

specifies the significance level (a value between 0 and 1) for removing an explanatory variable from the model in the BACKWARD or STEPWISE method. For all variables in the model, the one with the largest p-value is removed if the p-value exceeds the specified significance level. The default value is 0.05.

START=n

begins the FORWARD, BACKWARD, or STEPWISE selection process with the first n effects listed in the MODEL statement. The value of n ranges from 0 to s, where s is the total number of effects in the MODEL statement. The default value of n is s for the BACKWARD method and 0 for the FORWARD and STEPWISE methods. Note that START=n specifies only that the first n effects appear in the first model, while INCLUDE=n requires that the first n effects be included in every model. For the SCORE method, START=n specifies that the smallest models contain n effects, where n ranges from 1 to s; the default value is 1. The START= option has no effect when SELECTION=NONE.

STOP=n

specifies the maximum (FORWARD method) or minimum (BACKWARD method) number of effects to be included in the final model. The effect selection process is stopped when n effects are found. The value of n ranges from 0 to s, where s is the total number of effects in the MODEL statement. The default value of n is s for the FORWARD method and 0 for the BACKWARD method. For the SCORE method, STOP=n specifies that the smallest models contain n effects, where n ranges from 1 to s; the default value of n is s. The STOP= option has no effect when SELECTION=NONE or STEPWISE.

STOPRES

SR

specifies that the addition and deletion of variables be based on the result of the likelihood score test for testing the joint significance of variables not in the model. This score chi-square statistic is referred to as the residual chi-square. In the FORWARD method, the STOPRES option enters the explanatory variables into the model one at a time until the residual chi-square becomes insignificant (that is, until the p-value of the residual chi-square exceeds the SLENTRY= value). In the BACKWARD method, the STOPRES option removes variables from the model one at a time until the residual chi-square becomes significant (that is, until the p-value of the residual chi-square becomes less than the SLSTAY= value). The STOPRES option has no effect for the STEPWISE method.

TYPE1

requests that a Type 1 (sequential) analysis of likelihood ratio test be performed. This consists of sequentially fitting models, beginning with the null model and continuing up to the model specified in the MODEL statement. The likelihood ratio statistic for each successive pair of models is computed and displayed in a table.

TYPE3 <(keywords)>

requests a Type 3 test for each effect that is specified in the MODEL statement. The default is to use the Wald statistic, but you can requests other statistics by specifying one or more of the following keywords:

ALL: requests the likelihood ratio tests, the score tests, and the Wald tests. Specifying TYPE3(ALL) is equivalent to specifying TYPE3=(LR SCORE WALD).
NONE: suppresses the Type 3 analysis. Even if the TYPE3 option is not specified, PROC PHREG displays the Wald test results for each model effect if a CLASS variable is involved in a MODEL effect. The NONE option can be used to suppress such display.
LR: requests the likelihood ratio tests. This request is not honored if the COVS option is also specified.
SCORE: requests the score tests. This request is not honored if the COVS option is also specified.
WALD: requests the Wald tests.

TIES=method

specifies how to handle ties in the failure time. The following methods are available:

BRESLOW

uses the approximate likelihood of Breslow (1974). This is the default value.

DISCRETE

replaces the proportional hazards model by the discrete logistic model

$\frac{\lambda (t;\mb {z})}{1-\lambda (t;\mb {z})} =\frac{\lambda _{0}(t)}{1-\lambda _{0}(t)} \ \mr {exp}(\mb {z’}{\bbeta })$

where $\lambda _{0}(t)$ and $h(t;\mb {z})$ are discrete hazard functions.

EFRON

uses the approximate likelihood of Efron (1977).

EXACT

computes the exact conditional probability under the proportional hazards assumption that all tied event times occur before censored times of the same value or before larger values. This is equivalent to summing all terms of the marginal likelihood for $\bbeta$ that are consistent with the observed data (Kalbfleisch and Prentice, 1980; DeLong, Guirguis, and So, 1994).

The EXACT method can take a considerable amount of computer resources. If ties are not extensive, the EFRON and BRESLOW methods provide satisfactory approximations to the EXACT method for the continuous time-scale model. In general, Efron’s approximation gives results that are much closer to the EXACT method results than Breslow’s approximation does. If the time scale is genuinely discrete, you should use the DISCRETE method. The DISCRETE method is also required in the analysis of case-control studies when there is more than one case in a matched set. If there are no ties, all four methods result in the same likelihood and yield identical estimates. The default, TIES=BRESLOW, is the most efficient method when there are no ties.

XCONV=value CONVEREPARM=value

specifies the relative parameter convergence criterion. Termination requires a small relative parameter change in subsequent iterations,

$\max _ i |\delta _ k^{(i)}| < \mi {value}$

where

$\displaystyle \delta _ k^{(i)} = \left\{ \begin{array}{ll} \theta _ k^{(i)} - \theta _{k-1}^{(i)} & |\theta _{k-1}^{(i)}| < .01 \\ \frac{\theta _ k^{(i)} - \theta _{k-1}^{(i)}}{\theta _{k-1}^{(i)} } & \textrm{otherwise} \end{array} \right.$

where $\theta _ k^{(i)}$ is the estimate of the ith parameter at iteration k.